
1976 年,一个瑞士计算机科学家写一本书《Algorithms + Data Structures = Programs》。即:算法 + 数据结构 = 程序。40 多年过去了,这个等式依然成立。
很多代码面试题都要求候选者深入理解数据结构,不管你来自大学计算机专业还是编程培训机构,也不管你有多少年编程经验。有时面试题会直接提到数据结构,比如“给我实现一个二叉树”,然而有时则不那么明显,比如“统计一下每个作者写的书的数量”。
什么是数据结构?数据结构是计算机存储、组织数据的方式。对于特定的数据结构(比如数组),有些操作效率很高(读某个数组元素),有些操作的效率很低(删除某个数组元素)。程序员的目标是为当前的问题选择最优的数据结构。
为什么我们需要数据结构?数据是程序的核心要素,因此数据结构的价值不言而喻。无论你在写什么程序,你都需要与数据打交道,比如员工工资、股票价格、杂货清单或者电话本。在不同场景下,数据需要以特定的方式存储,我们有不同的数据结构可以满足我们的需求。
8 种常用数据结构数组
栈
队列
链表
图
树
前缀树
哈希表
1. 数组数组(Array)大概是最简单,也是最常用的数据结构了。其他数据结构,比如栈和队列都是由数组衍生出来的。
下图展示了 1 个数组,它有 4 个元素:

每一个数组元素的位置由数字编号,称为下标或者索引(index)。大多数编程语言的数组第一个元素的下标是 0。
根据维度区分,有 2 种不同的数组:
一维数组(如上图所示)
多维数组(数组的元素为数组)
数组的基本操作Insert - 在某个索引处插入元素
Get - 读取某个索引处的元素
Delete - 删除某个索引处的元素
Size - 获取数组的长度
常见数组代码面试题查找数组中第二小的元素
查找第一个没有重复的数组元素
合并 2 个排序好的数组
重新排列数组中的正数和负数
2. 栈撤回,即 Ctrl+Z,是我们最常见的操作之一,大多数应用都会支持这个功能。你知道它是怎么实现的吗?答案是这样的:把之前的应用状态(限制个数)保存到内存中,最近的状态放到第一个。这时,我们需要栈(stack)来实现这个功能。
栈中的元素采用 LIFO (Last In First Out),即后进先出。
下图的栈有 3 个元素,3 在最上面,因此它会被第一个移除:
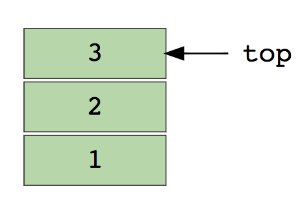
Push — 在栈的最上方插入元素
Pop — 返回栈最上方的元素,并将其删除
isEmpty — 查询栈是否为空
Top — 返回栈最上方的元素,并不删除
常见的栈代码面试题使用栈计算后缀表达式
使用栈为栈中的元素排序
检查字符串中的括号是否匹配正确
3. 队列队列(Queue)与栈类似,都是采用线性结构存储数据。它们的区别在于,栈采用 LIFO 方式,而队列采用先进先出,即FIFO(First in First Out)。
下图展示了一个队列,1 是最上面的元素,它会被第一个移除:
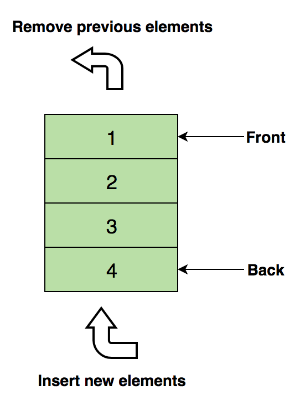
Enqueue — 在队列末尾插入元素
Dequeue — 将队列第一个元素删除
isEmpty — 查询队列是否为空
Top — 返回队列的第一个元素
常见的队列代码面试题使用队列实现栈
倒转队列的前 K 个元素
使用队列将 1 到 n 转换为二进制
4. 链表链表(Linked List)也是线性结构,它与数组看起来非常像,但是它们的内存分配方式、内部结构和插入删除操作方式都不一样。
链表是一系列节点组成的链,每一个节点保存了数据以及指向下一个节点的指针。链表头指针指向第一个节点,如果链表为空,则头指针为空或者为 null。
链表可以用来实现文件系统、哈希表和邻接表。
下图展示了一个链表,它有 3 个节点:

链表分为 2 种:
单向链表
双向链表
链表的基本操作InsertAtEnd — 在链表结尾插入元素
InsertAtHead — 在链表开头插入元素
Delete — 删除链表的指定元素
DeleteAtHead — 删除链表第一个元素
Search — 在链表中查询指定元素
isEmpty — 查询链表是否为空
常见的队列代码面试题倒转 1 个链表
检查链表中是否存在循环
返回链表倒数第 N 个元素
移除链表中的重复元素
5. 图图(graph)由多个节点(vertex)构成,节点之间阔以互相连接组成一个网络。(x, y)表示一条边(edge),它表示节点 x 与 y 相连。边可能会有权值(weight/cost)。
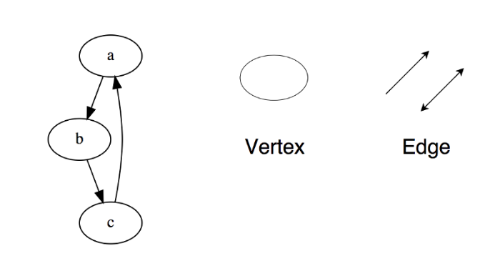
图分为两种:
无向图
有向图
在编程语言中,图有可能有以下两种形式表示:
邻接矩阵(Adjacency Matrix)
邻接表(Adjacency List)
遍历图有两周算法
广度优先搜索(Breadth First Search)
深度优先搜索(Depth First Search)
常见的图代码面试题实现广度优先搜索
实现深度优先搜索
检查图是否为树
统计图中边的个数
使用 Dijkstra 算法查找两个节点之间的最短距离
6. 树树(Tree)是一个分层的数据结构,由节点和连接节点的边组成。树是一种特殊的图,它与图最大的区别是没有循环。
树被广泛应用在人工智能和一些复杂算法中,用来提供高效的存储结构。
下图是一个简单的树以及与树相关的术语:

树有很多分类:
N 叉树(N-ary Tree)
平衡树(Balanced Tree)
二叉树(Binary Tree)
二叉查找树(Binary Search Tree)
平衡二叉树(AVL Tree)
红黑树(Red Black Tree)
2-3 树(2–3 Tree)
其中,二叉树和二叉查找树是最常用的树。
常见的树代码面试题计算树的高度
查找二叉平衡树中第 K 大的元素
查找树中与根节点距离为 k 的节点
查找二叉树中某个节点所有祖先节点
7. 前缀树
