数据结构 - 堆(Heap)
1.堆的定义
堆的形式满足完全二叉树的定义:
若 i < ceil(n/2) ,则节点i为分支节点,否则为叶子节点
叶子节点只可能在最大的两层出现,而最大层次上的叶子节点都依次排列在该层最左侧的位置上
如果有度为1的节点,那么只可能有一个,且该节点只有左孩子
根据堆定义的不同,分为大根堆和小根堆:
大根堆每个节点的值都大于其子节点的值
小根堆每个节点的值都小于其子节点的值
除此之外还有一个重要的内容:
单节点也符合堆的特质
2.堆的初始化
堆的初始化可以可以分为如下几个步骤(以初始化最大根堆为例):
首先初始化为完全二叉树形式。
从最后一个具有孩子节点的节点进行调整,如果以该元素为根的子树是最大根堆,则不进行操作,否则将该子树调整为最大根堆(调整思路为不断与子节点进行比较和交换,直至满足最大根堆要求为止)。
数组:[2,7,26,25,19,17,90,3],初始化为完全二叉树形式。
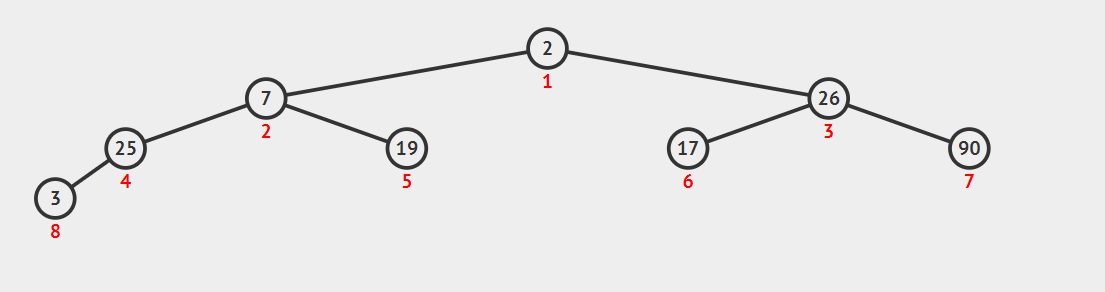
调整最后一个具有孩子节点的节点[4],符合最大根堆要求,不进行操作。

调整节点[3],以满足最大根堆要求,交换[3]和[7]。
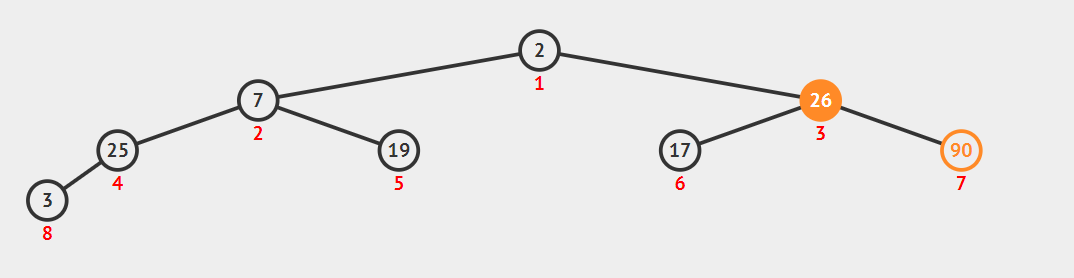
调整节点[2],以满足最大根堆要求,交换[2]和[5]。

调整节点[1],以满足最大根堆要求,交换[1]和[3]后继续交换[3]和[7],最终完成初始化,满足最大根堆要求。

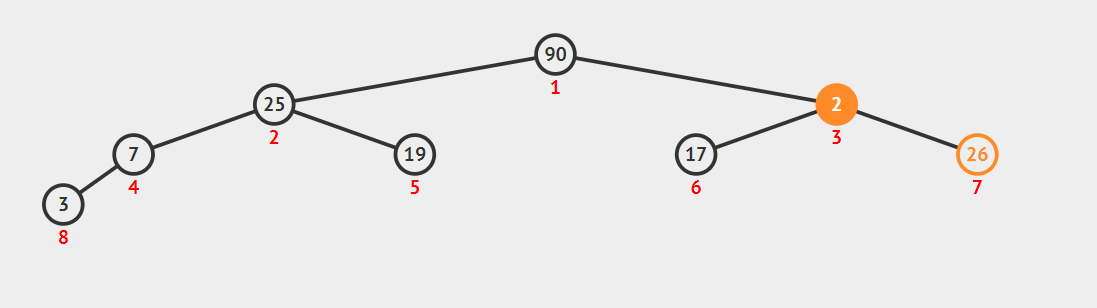

3.堆节点的插入和调整
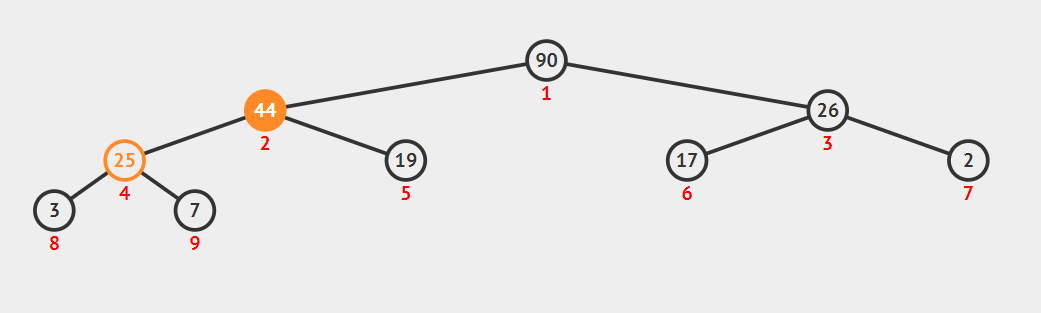
如上图所示,在如上所示图中插入44


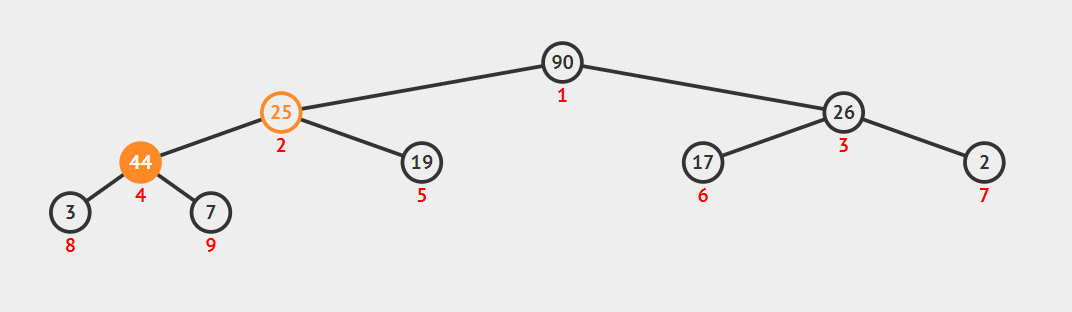
堆的初始化和插入的C++语言代码描述
/** *@Author : Kindear *@Intro : DataStrcut C++ Code 以最大根堆为例 **/ #include <bits/stdc++.h> #define ARR_SIZE 20 using namespace std; typedef int ElementType; void AdjustUp(ElementType A[],int k, int len) //该方法用于堆插入调整 { int Tmp = A[k]; //暂存k位置的数值 int i = k/2; //父节点的下标 while(i > 0 && A[i] < Tmp) { //如果该节点大于父节点,那么就交换两者的位置,满足最大根堆的要求 A[k] = A[i]; k = i; i = k/2; //继续向上寻找并调整,直至满足最大根堆要求 } A[k] = Tmp; // } void AdjustDown(ElementType A[],int k,int len) //该方法用于堆的初始化 { int Tmp = A[k]; for(int i = 2*k; i <= len; i*=2) //向下筛选 { if(i < len && A[i] < A[i+1]) i++; if(Tmp > A[i]) break; else { A[k] = A[i]; k = i; } } A[k] = Tmp; } void BuildMaxHeap(ElementType A[],int len) { for(int i= len/2 ; i > 0; i--) { AdjustDown(A,i,len); } } void PrintfElementArray(ElementType A[],int len) { for(int i=1;i<=len;i++) { printf("%d%c",A[i],i==len?'\n':' '); } } int main() { ElementType A[] = {0,2,7,26,25,19,17,90,3}; ElementType B[ARR_SIZE]; BuildMaxHeap(A,8); PrintfElementArray(A,8); for(int i=0;i<=8;i++) { B[i] = A[i]; } B[9] = 44;//插入44 AdjustUp(B,9,9); PrintfElementArray(B,9); } 参考文档[1] 数据结构堆可视化:https://visualgo.net/zh/heap

