解法二的实现方式与解法一有点不同,按照功能的不同,解法二将两个栈一个用于入队,一个用于出队。假设栈 inStack 用于实现入队操作,栈 outStack 用于实现出队操作。下面对入队、出队等操作的底层实现分别进行讲解。
入队(push)入队操作比较简单,直接将新的元素压入栈 inStack 中,同时,对于第一个进入栈中的元素,我们用一个变量 front 保存起来,用于表示栈 inStack 这个队列的队首。
/** Push element x to the back of queue. */ public void push(int x) { if (inStack.empty()) { front = x; } inStack.push(x); }复杂度分析如下:
时间复杂度:\(O(1)\)
空间复杂度:\(O(n)\),需要额外的空间用于存储队列元素
出队(pop)在入队时,由于先入的元素处于输入栈 inStack 的栈底,因此,为了能够弹出栈底的元素实现出队操作,需要将输入栈 inStack 中的元素弹出并压入到输出栈 outStack 中。此时,输出栈 outStack 中元素的出栈顺序和队列的出队顺序是一致的。只要输出栈 outStack 中还有元素,每次执行出队操作只需要将栈 outStack 的栈顶元素弹出即可。当输出栈 outStack 为空时,执行出队操作则需要先将输入栈 inStack 中的元素弹出并压入输出栈。详细的步骤如图2所示。
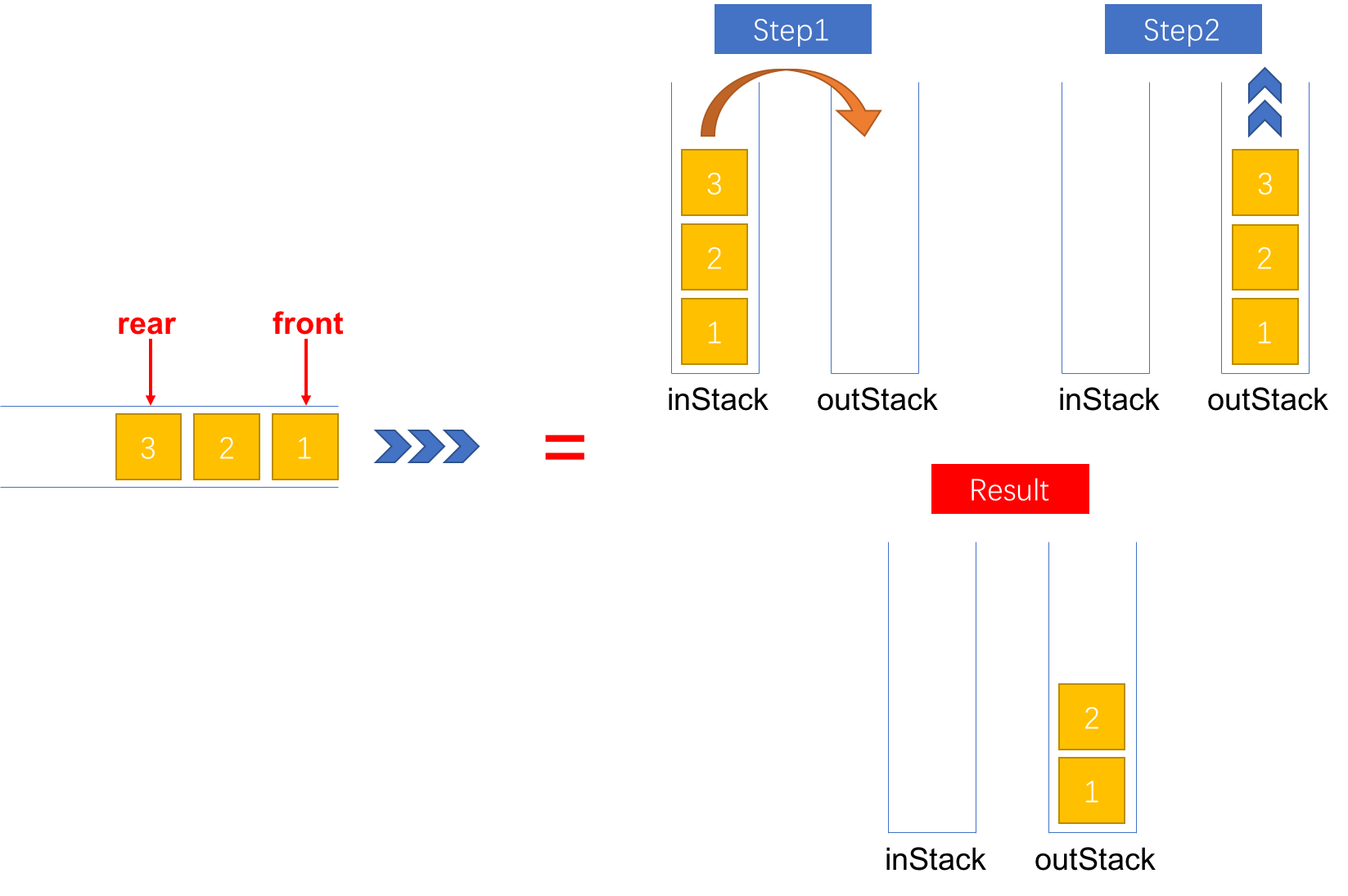
图2:将一个元素出队
代码(Java)实现如下。
/** Removes the element from in front of queue and returns that element. */ public int pop() { if (empty()) { throw new IllegalArgumentException("[ERROR] The queue is empty!"); } if (outStack.isEmpty()) { while (!inStack.isEmpty()) { outStack.push(inStack.pop()); } } return outStack.pop(); }复杂度分析如下:
时间复杂度:均摊时间复杂度为 \(O(1)\),最坏情况下,时间复杂度为 \(O(n)\),更为详细的均摊复杂度分析可以查看官网的文章
空间复杂度:\(O(1)\)
查看队首(peek)与出队操作类似,当输出栈 outStack 不为空时,只需要返回输出栈 outStack 的栈顶元素即可。不同的是,由于我们用变量 front 存储了输入栈最先进入的元素,因此,当输出栈 outStack 为空时,不需要再将输入栈 inStack 的元素弹出并压入到输出栈 outStack 中便可以得到当前队首的元素。
/** Get the front element. */ public int peek() { if (empty()) { throw new IllegalArgumentException("[ERROR] The queue is empty!"); } if (!outStack.isEmpty()) { return outStack.peek(); } else { return front; } }复杂度分析如下:
时间复杂度:\(O(1)\),借助于变量 front,可以使得 peek 操作在任意情况下都是 \(O(1)\) 的时间复杂度
空间复杂度:\(O(1)\)
是否为空(empty)由于两个都有可以存在元素,因此,要判断队列是否为空,需要同时判断两个栈。
/** Returns whether the queue is empty. */ public boolean empty() { return inStack.isEmpty() && outStack.isEmpty(); }复杂度分析如下:
时间复杂度:\(O(1)\)
空间复杂度:\(O(1)\)
Java 实现 class MyQueue { /** * The stack used to implement enqueue functionality */ private Stack<Integer> inStack; /** * The stack used to implement dequeue functionality */ private Stack<Integer> outStack; /** * The front element in the stack `inStack` 's queue */ private int front; /** Initialize your data structure here. */ public MyQueue2() { inStack = new Stack<>(); outStack = new Stack<>(); } /** Push element x to the back of queue. */ public void push(int x) { if (inStack.empty()) { front = x; } inStack.push(x); } /** Removes the element from in front of queue and returns that element. */ public int pop() { if (empty()) { throw new IllegalArgumentException("[ERROR] The queue is empty!"); } if (outStack.isEmpty()) { while (!inStack.isEmpty()) { outStack.push(inStack.pop()); } } return outStack.pop(); } /** Get the front element. */ public int peek() { if (empty()) { throw new IllegalArgumentException("[ERROR] The queue is empty!"); } if (!outStack.isEmpty()) { return outStack.peek(); } else { return front; } } /** Returns whether the queue is empty. */ public boolean empty() { return inStack.isEmpty() && outStack.isEmpty(); } } Python 实现 class MyQueue: def __init__(self): """ Initialize your data structure here. """ self._in_stack, self._out_stack, self._front = [], [], None def push(self, x): """ Push element x to the back of queue. :type x: int :rtype: void """ if not self._in_stack: self._front = x self._in_stack.append(x) def pop(self): """ Removes the element from in front of queue and returns that element. :rtype: int """ if self.empty(): raise Exception("[ERROR] The queue is empty!") if not self._out_stack: while self._in_stack: self._out_stack.append(self._in_stack.pop()) return self._out_stack.pop() def peek(self): """ Get the front element. :rtype: int """ if self.empty(): raise Exception("[ERROR] The queue is empty!") if not self._out_stack: return self._front else: return self._out_stack[-1] def empty(self): """ Returns whether the queue is empty. :rtype: bool """ return not self._in_stack and not self._out_stack
