Given a binary tree, return the zigzag level order traversal of its nodes’ values. (ie, from left to right, then right to left for the next level and alternate between).给定一棵二叉树,从顶向下,进行Z字形分层遍历,即:如果本层是从左向右的,下层就是从右向左。
流程与 BFS 类似,就是多了个用于区分左右的 flag
对于不为空的结点,先把该结点加入到队列中
从队中拿出结点,如果该结点的左右结点不为空,就分别把左右结点加入到队列中
将 isFromLeft 值取反
重复以上操作直到队列为空
视频同样的这个体型太特殊,所以没有相关视频解析,不过好在算法过程也很好理解
public List<List<Integer>> zigzagLevelOrder(TreeNode root) { List<List<Integer>> result = new ArrayList<>(); if (root == null){ return result; } Queue<TreeNode> queue = new LinkedList<>(); queue.offer(root); boolean isFromLeft = false; while(!queue.isEmpty()){ int size = queue.size(); isFromLeft = !isFromLeft; List<Integer> list = new ArrayList<>(); for(int i = 0; i < size; i++){ TreeNode node; if (isFromLeft){ node = queue.pollFirst(); }else{ node = queue.pollLast(); } list.add(node.val); if (isFromLeft){ if (node.left != null){ queue.offerLast(node.left); } if (node.right != null){ queue.offerLast(node.right); } }else{ if (node.right != null){ queue.offerFirst(node.right); } if (node.left != null){ queue.offerFirst(node.left); } } } result.add(list); } return result; }### 左右翻转
这是一道华为面试原题,题目大意是:
输入二叉树如下:
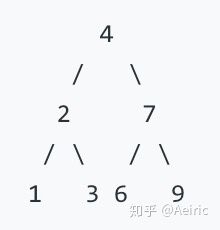
反转后输出:

乍一看很难办,其实想一个解决方案很简单,这里我直接举三个方案:
方法一:比如我们用递归的思路,本质思想是:本质思想也是左右节点进行交换
交换前递归调用对根结点的左右节点分别进行处理
保证交换前左右节点已经翻转。
三步搞定,我们看下代码实现:
public TreeNode invertTree(TreeNode root) { if (root == null) { return null; } Stack<TreeNode> stack = new Stack<>(); stack.push(root); while(!stack.isEmpty()) { final TreeNode node = stack.pop(); final TreeNode left = node.left; node.left = node.right; node.right = left; if(node.left != null) { stack.push(node.left); } if(node.right != null) { stack.push(node.right); } } return root; } 方法二:循环,队列存储(BFS,非递归)本质思想是:
左右节点进行交换
循环翻转每个节点的左右子节点
将未翻转的子节点存入队列中
循环直到栈里所有节点都循环交换完为止。
public TreeNode invertTree(TreeNode root) { if (root == null) { return null; } Queue<TreeNode> queue = new LinkedList<>(); queue.offer(root); while (!queue.isEmpty()) { TreeNode node = queue.poll(); TreeNode left = node.left; node.left = node.right; node.right = left; if (node.left != null) { queue.offer(node.left); } if (node.right != null) { queue.offer(node.right); } } return root; } 方法三:「压轴出场,三步秒杀」递归本质思想是:
左右节点进行交换
交换前递归调用对根结点的左右节点分别进行处理
保证交换前左右节点已经翻转。
同样三步搞定,我们看下代码:
public void invert(TreeNode root) { if (root == null) { return; } TreeNode temp = root.left; root.left = root.right; root.right = temp; invert(root.left); invert(root.right); }乍一看,是到送分题。我第一眼的想法就是:在方法中定义max用来保存遍历得到的最大值,结果每次递归时,都等于在重新定义max,这种方法不对。所以怎么办?
采用分治思想
从整棵树的底部开始
两两比较,放回最大值
看一眼算法你就懂了
public int getMax(TreeNode root) { if (root == null) { return Integer.MIN_VALUE; } else { int left = getMax(root.left); int right = getMax(root.right); return Math.max(Math.max(left, rigth), root.val); } }深度问题和最大值一样,容易想复杂,其实非常简单,也可以看作一种分治的思想
二叉树的最大深度是距根节点路径最长的某一树叶节点的深度。
二叉树的深度等于二叉树的高度,也就等于根节点的高度。根节点的高度为左右子树的高度较大者+1。
视频【算法面试题】求二叉树最大的深度
public int maxDepth(TreeNode root) { if (root == null) { return 0; } int left = maxDepth(root.left); int right = maxDepth(root.right); return Math.max(left, right) + 1; }这道题目太常见了,当我一看到题目时就错了:
题目:最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明: 叶子节点是指没有子节点的节点。
看到了吧,这时就得明确正确的递归结束条件
举个例子:很多人写出的代码都不符合 1,2 这个测试用例,是因为没搞清楚题意
题目中说明: 叶子节点是指没有子节点的节点,这句话的意思是 1 不是叶子节点
题目问的是到叶子节点的最短距离,所以所有返回结果为 1 当然不是这个结果
另外这道题的关键是搞清楚递归结束条件
叶子节点的定义是左孩子和右孩子都为 null 时叫做叶子节点
当 root 节点左右孩子都为空时,返回 1
当 root 节点左右孩子有一个为空时,返回不为空的孩子节点的深度
当 root 节点左右孩子都不为空时,返回左右孩子较小深度的节点值
视频
