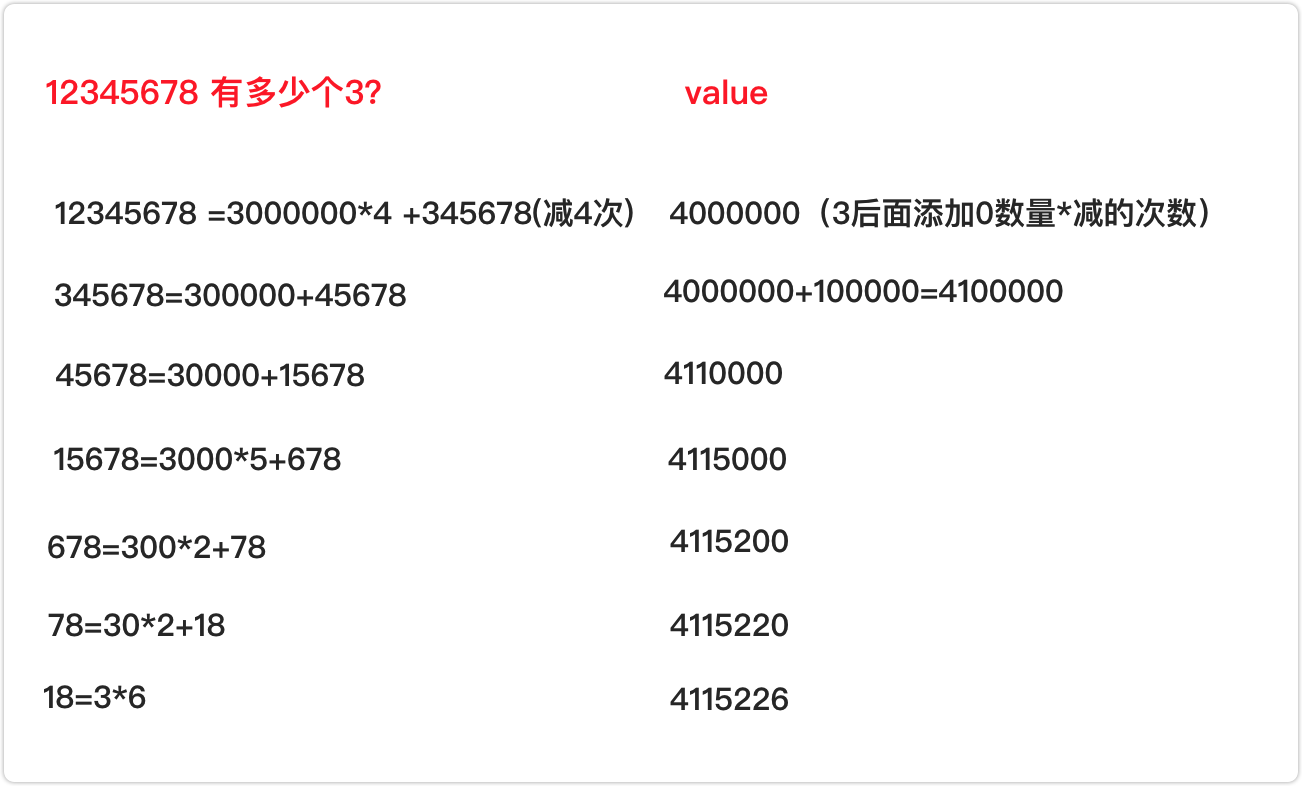
这题在力扣上没有原题,但是可以在小米OJ【大数相减】上验证自己代码的正确性,具体实现的代码为:
public static boolean compare(String num1,String num2) { if(num1.length()<num2.length()) return false; else if(num1.length()>num2.length()) return true; else return num1.compareTo(num2)>0; } public static String subtractString(String num1,String num2) { char sign='+';//正负号 //让num1>num2 如果num1<num2 那么结果就是—(num2-num1) //可以先将num1和num2交换和前面情况统一 if(!compare(num1,num2)) { sign='-'; String team = num2; num2 = num1; num1 = team; } int len1=num1.length()-1; int len2=num2.length()-1; char ch1[] = num1.toCharArray(); char ch2[] = num2.toCharArray(); StringBuilder sb=new StringBuilder(); int borrow=0;//借位 while (len1>=0||len2>=0) { int n1=len1>=0?(ch1[len1--]-'0'):0; int n2=len2>=0?(ch2[len2--]-'0'):0; int num=n1-n2-borrow; borrow=0; if(num<0)//需要向前借位 { borrow=1; num+=10; } sb.append(num); } sb=sb.reverse();//需要先翻转 int index = 0;//去掉前面没用的’0‘ while (index<sb.length()&&sb.charAt(index) == '0') { index++; } //如果两个数相同 直接返回"0" if(index==sb.length()) return "0"; if(sign=='+')//如果正数 return sb.substring(index); else return sign+sb.substring(index);//负数需要返回 } 大数乘法大数乘法乍一想可能比较复杂,因为乘法比起加法可能进位不光是1,还有两个数各种位置都需要相乘计算,这时候就需要我们化繁为简了。
多*多考虑起来可能有些麻烦,但是如果多*一考虑起来呢?如果是多位乘以一位数,那么就拿一位的分别乘以多位数的个位、十位、百位,在计算的同时考虑一下进位的情况。
但是也可以先直接用int类型数组存储各位的乘积然后从右向左进行进位,如下图所示。
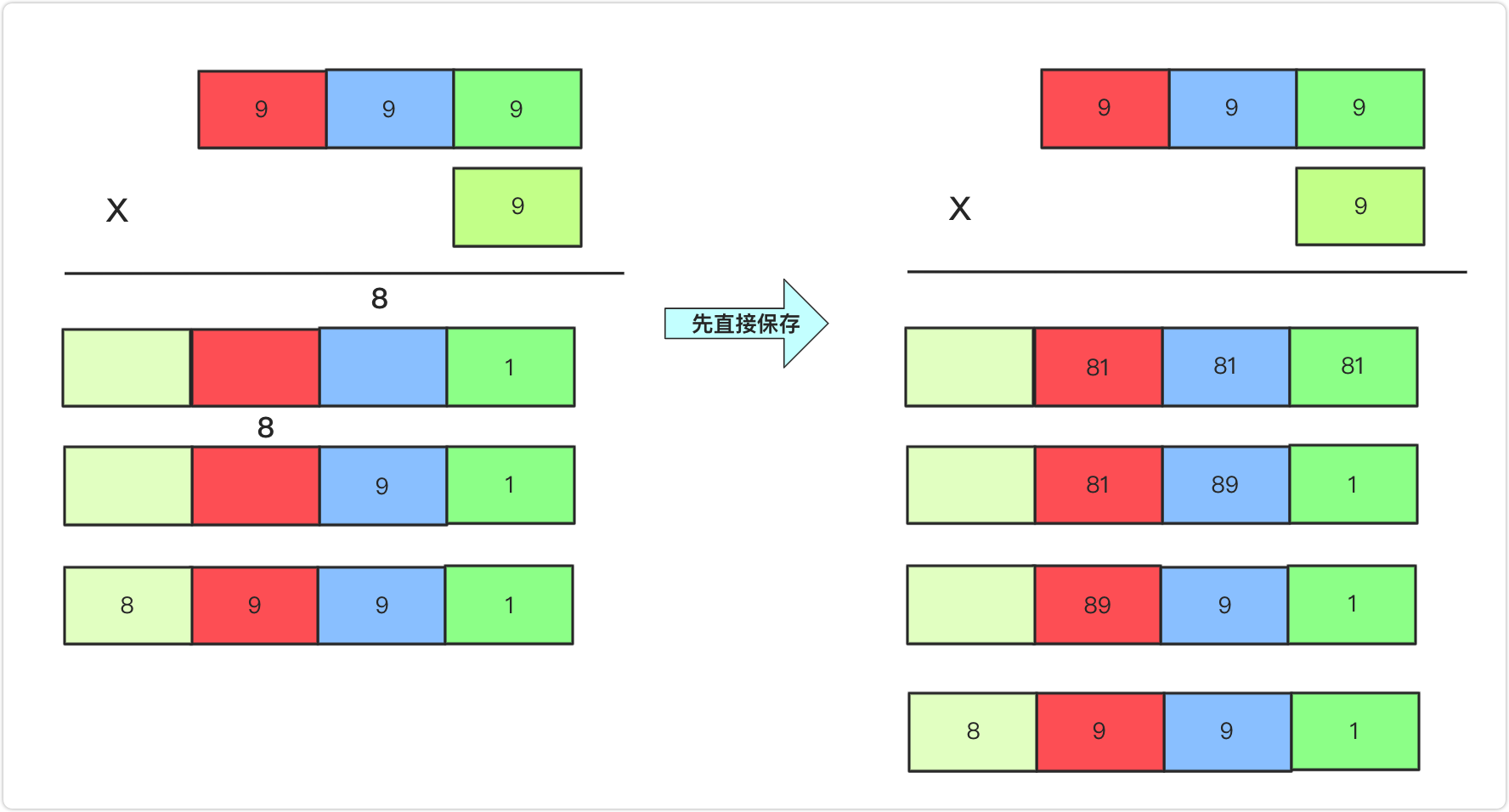
而多*多 也是这个道理,将不同位乘积先叠加到对应位置上,然后从右向左进位,一直到不需要进位为止。
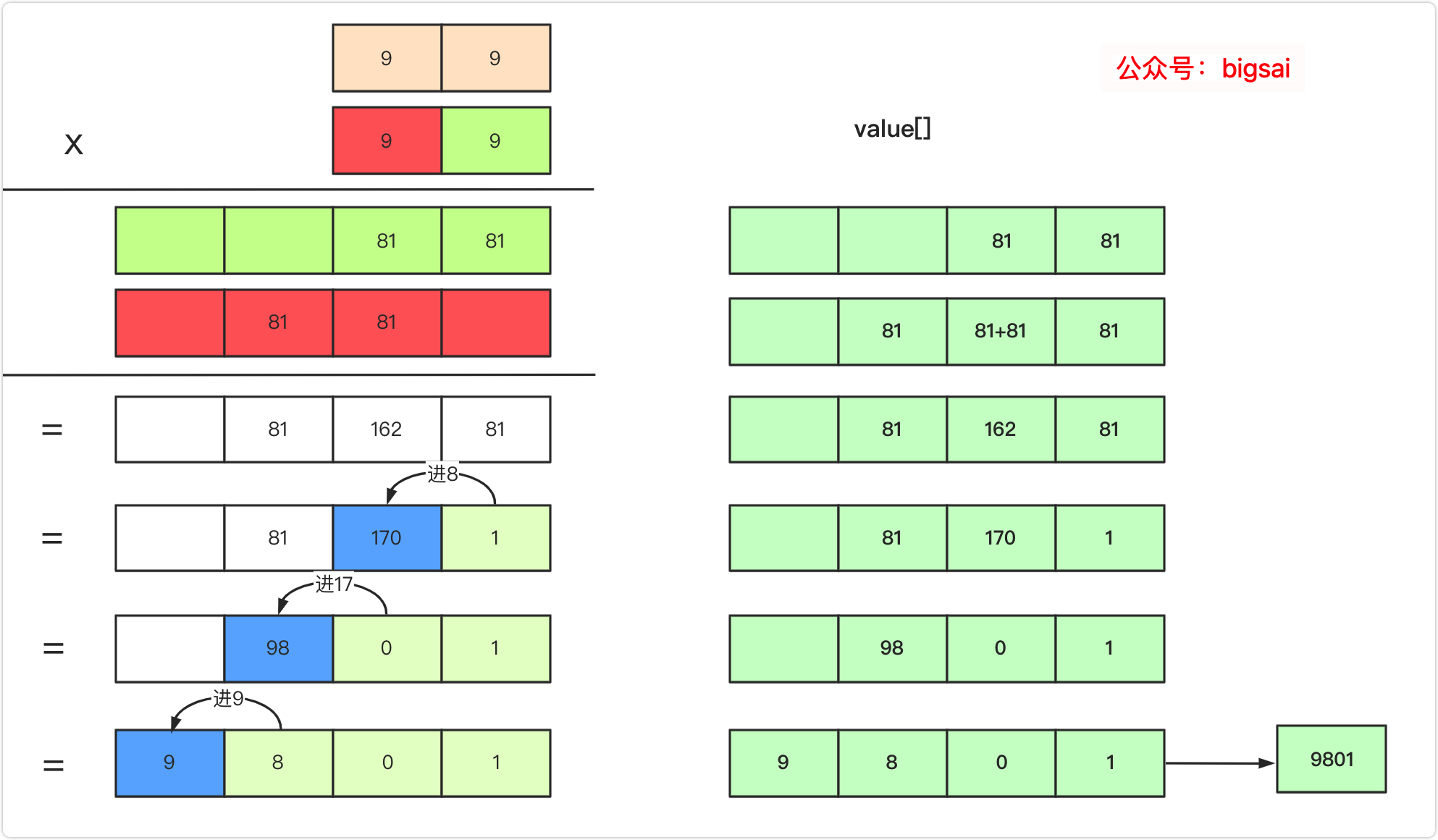
你可能会疑问,如果两个数组的长度分别为a和b这个数组到底该开多大呢?
a+b大小就够了,怎么分析呢?其中一个a不变。另一个b变成最小b+1数字即十的倍数,那么这样在相乘的时候也不过是a+b长度,所以这里a+b长度就够了。
这题有力扣对应题可以去试试【43字符串相乘】,具体代码位:
public String multiply(String num1, String num2) { if("0".equals(num1)||"0".equals(num2))return "0"; char a[]=num1.toCharArray(); char b[]=num2.toCharArray(); int value[]=new int[a.length+b.length]; for(int i=a.length-1;i>=0;i--) { for(int j=b.length-1;j>=0;j--) { int index=a.length-1-i+b.length-1-j; value[index]+=(a[i]-'0')*(b[j]-'0'); } } for(int i=0;i<value.length-1;i++) { value[i+1]+=value[i]/10; value[i]=value[i]%10; } int index=value.length-1; while(value[index]==0) {index--;} StringBuilder sBuilder=new StringBuilder(); while (index>=0) { sBuilder.append(value[index--]); } return sBuilder.toString(); } 大数除法大数加减乘都搞定了,通过模拟来实现,但是大数除法也通过模拟来实现?
并不是,对于大数a/b,一般最多要求求到其整数解或者余数,即a/b=c……d(a,b,c,d均为整);也就是a里面有c个b,并且还剩下d。核心是先求c是多少,对于程序来说,可以通过枚举啊,将除法变成减法,从a中不断减d,一直到不能减为止。
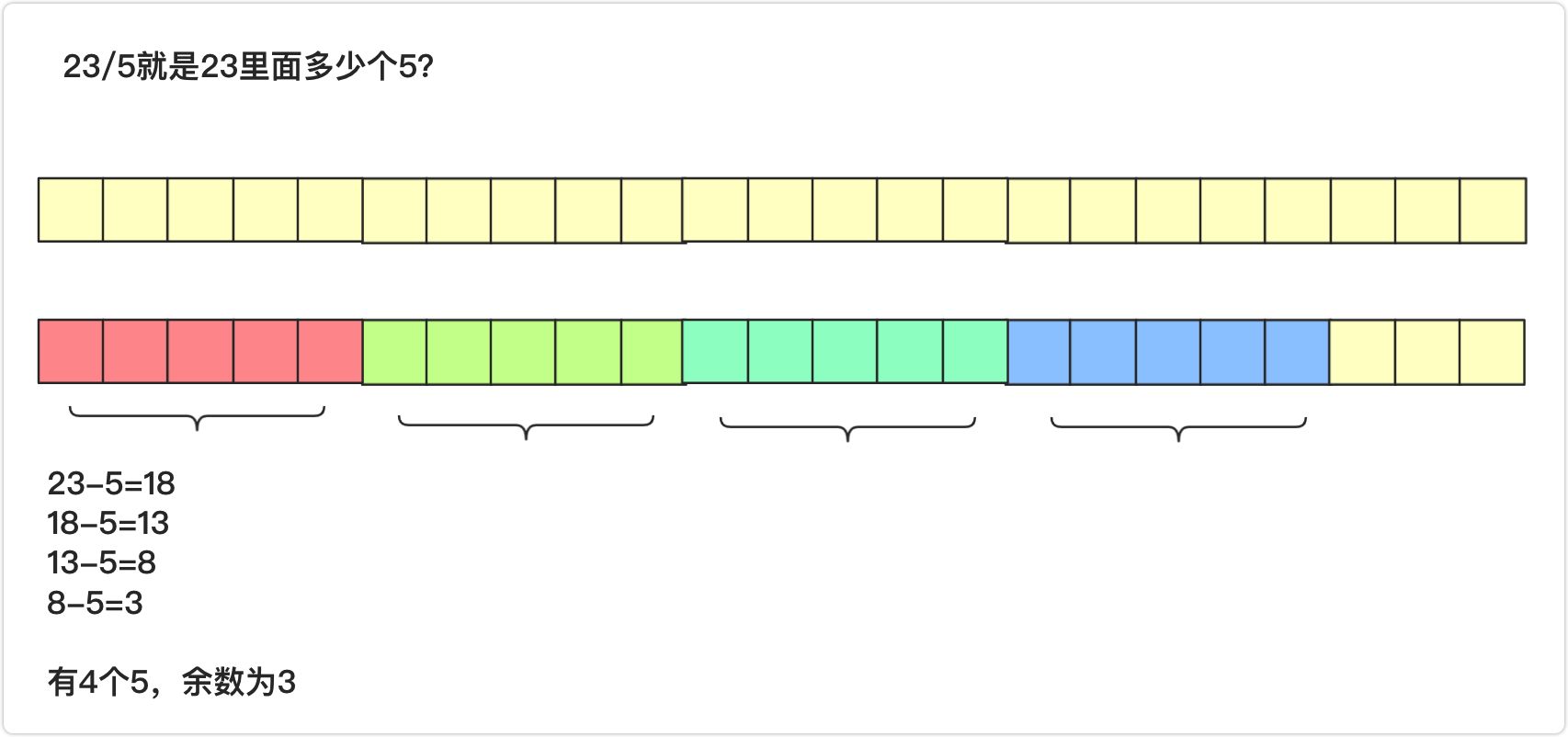
但是有个问题,如果被除数a很大很大,可能有居多个b,那么这样时间复杂度太高了,不可能执行那么多次,那么需要怎么样去优化这个方法呢?
那就要加速寻找次数,减少这个减法的次数了,减法次数减小的一个最好方案就是能不能扩大除数b。如果b后面加个'0',那么算出来的结果就乘以10,减法的次数变成原来十分之一。根据这个思想我们可以一直每次找到b的最大10的倍数(小于a)计算减的次数再换算成减b的总词数,将结果要以字符串方式保留,后面一直迭代到最后为止,这虽然是一道除法运算的题,但是也蕴涵减法和加法(次数叠加到结果中)。