原文地址: WebGL之物体选择
使用WebGL将图形绘制到画布后,如何与外部进行交互?这其中最关键的就是如何实现物体的选择。比如鼠标点击后判断是否选中了某个图形或图形的某个部分。
本节实现的效果: WebGL选中物体

如何实现选中物体 颜色区分法
《WebGL编程指南》中提出了一个原理很简单的解决方案,步骤如下:
鼠标按下时物体重绘为红色或其他能区分的颜色
读取鼠标点击处像素的颜色
gl.readPixels(x,y,width,height,format,type,pixels)使用物体原来的颜色进行重绘,以恢复物体本来颜色
判断第2步读取到的颜色是否与预设的颜色值相等,相等则表示点击中物体
可以说这是个非常容易实现的方案,不过要为每个物体分别设置不同的区分颜色却是个隐患,同时也不够友好。
光线投射法这是使用最广泛也最精确的一种方案了,Three.js 中的光线投射器 (Raycaster) 就实现了这种方案,可以看里面的源代码。
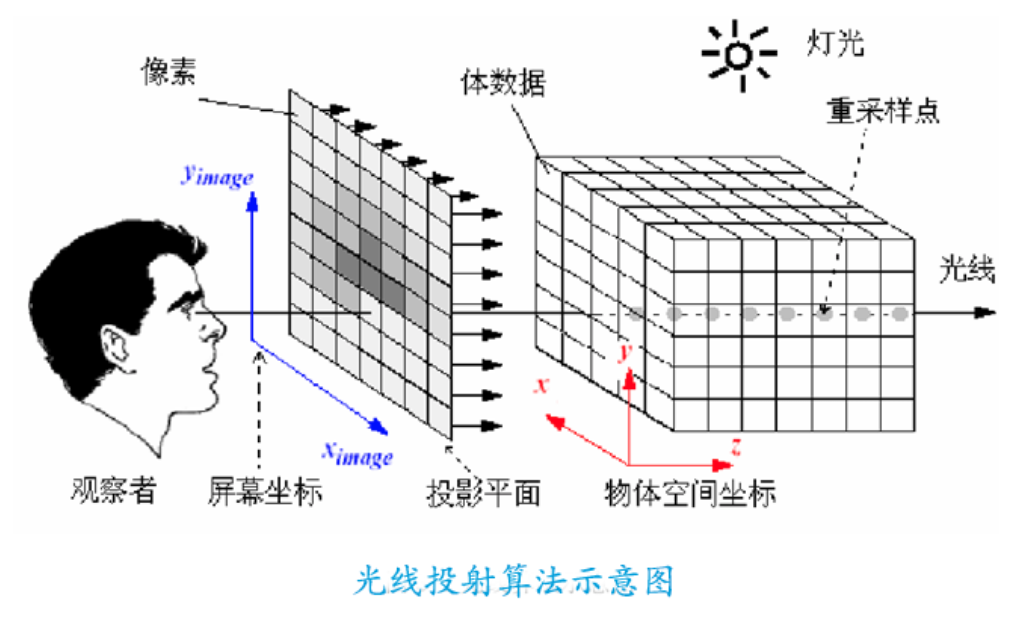
它的基本原理: 从视点出发的光线首先投射到近截面,最后投射到远截面,结合鼠标点击的位置 (x, y) 和视图投影矩阵 (viewProjection)。可以得出由近截面坐标 (x1, y1, z1) 和远截面坐标 (x2, y2, z2) 组成的光线向量。然后我们就可以将物体坐标构成的面逐个与这个光线向量进行对比。首先对比盒子边界,再对比三角形面,这中间涉及到法向量,点积,叉积的计算,那叫一个复杂。 投影坐标判断法
目前对光线投射的具体实现理解地不是很透彻,那我就只能通过自己的理解来实现个简单版的方案。基本原理就是,用视图投影模型矩阵 (mvp) 对图形坐标进行变换,得到在屏幕中的绘制坐标(xyz)。然后遍历每个坐标得出一个由最大最小xy坐标 (xmax, xmin, ymax, ymin) 构成的二维平面盒子。最后与鼠标位置 (x, y) 进行比较,如果鼠标xy坐标处于盒子边界之内,那么就可判断选中了该物体。核心代码如下:
canvas.addEventListener('mousemove', function(e) { //坐标转换为webgl表示区间 const pos = util.windowToWebgl(tCanvas,e.clientX,e.clientY); const ps = []; Polygons.forEach((p,i)=>{ //重置状态 p.select = false; //mvp矩阵 const matrix = m4.translate(viewProjection, p.pos); let xmax, ymax, xmin, ymin;//盒子的边界 //遍历顶点获取盒子的边界 for(let j = 0; j < p.position.length; j = j+3){ //对坐标进行矩阵转换 const s = m4.transformPoint(matrix, p.position.slice(j,j+3)); if(j == 0){ xmax = s[0]; xmin = s[0]; ymax = s[1]; ymin = s[1]; continue; } if(s[0]>xmax) xmax = s[0]; if(s[0]<xmin) xmin = s[0]; if(s[1]>ymax) ymax = s[1]; if(s[1]<ymin) ymin = s[1]; } // 位于盒子边界内 if(pos.x >= xmin && pos.x <= xmax && pos.y >= ymin && pos.y <= ymax){ ps.push(p); } }); if(!ps.length) return; let sel; //获取最靠近视点的图形 if(ps.length == 1) { sel = ps[0]; } else { sel = ps.sort((a,b)=> { const az = m4.transformPoint(a.matrix,[0,0,0])[2]; const bz = m4.transformPoint(b.matrix,[0,0,0])[2]; return az - bz; })[0]; } //设置该图形为选中 Polygons[sel.index].select = true; },false);目前实现的功能在 选择不规则的物体时,判断地不是很精准,毕竟不是所有的图形都是类似矩形。
那么解决方案就是:我们知道WebGL图形是由三角形构成的,如果进一步判断鼠标位置是否在构成该图形的三角形面当中,那就会更加精确了,这个功能留给读者去实现。

