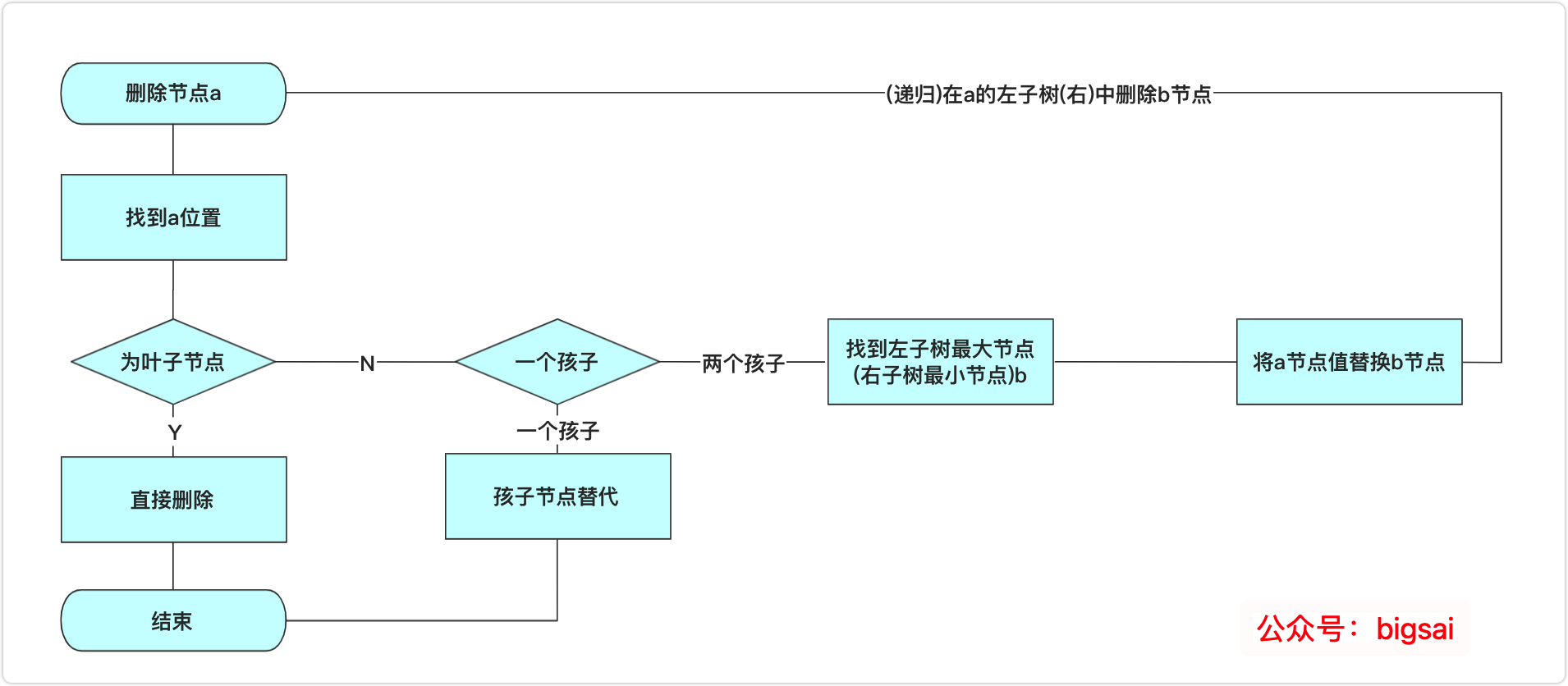
此种情况也很容易,直接将删除点的子节点放到被删除位置即可。

左右节点均不空
左右孩子节点都不为空这种情况是相对比较复杂的,因为不能直接用其中一个孩子节点替代当前节点(放不下,如果孩子节点也有两个孩子那么有一个节点无法放,例如拿下面71节点替代)
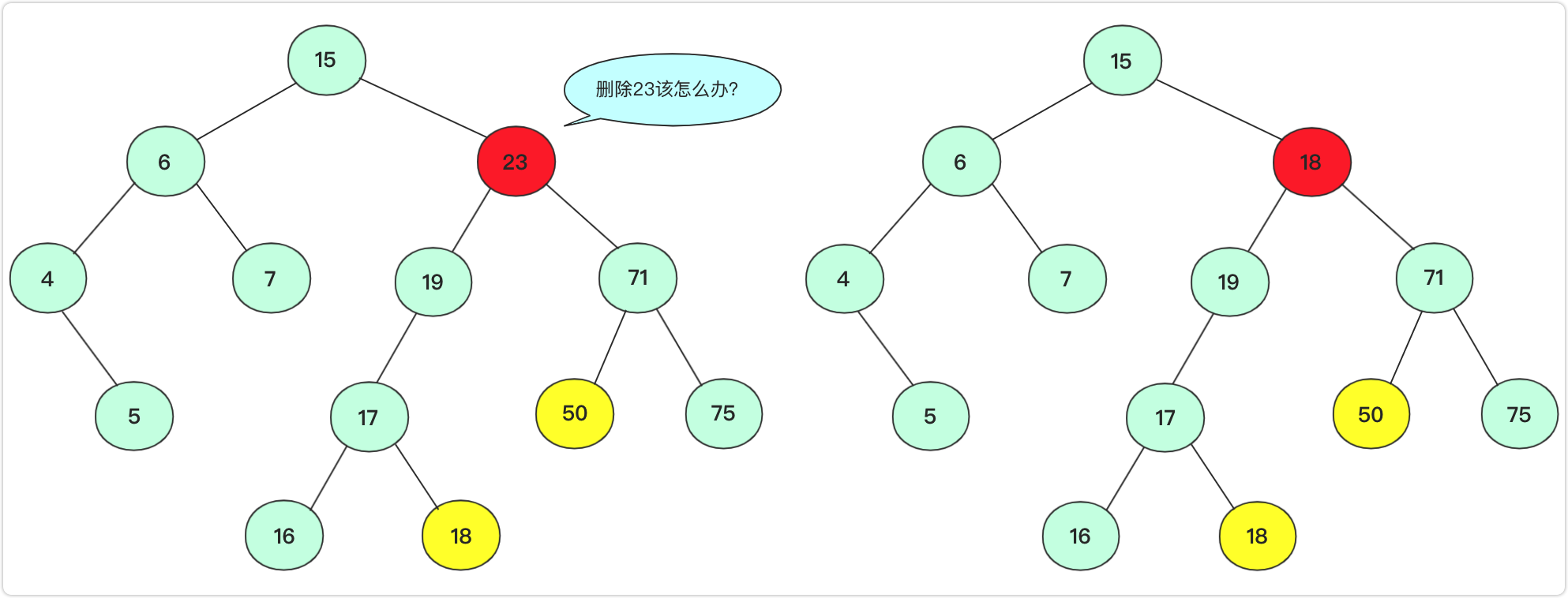
如果拿19或者71节点填补。虽然可以保证部分侧大于小于该节点,但是会引起合并的混乱.比如你若用71替代23节点。那么你需要考虑三个节点(19,50,75)之间如何处理,还要考虑他们是否满,是否有子女,这是个复杂的过程,不适合考虑。
所以,我们要分析我们要的这个点的属性:能够保证该点在这个位置仍满足二叉搜索树的性质(找到值最近的),那么子树中哪个节点满足这样的关系呢?
左子树中最右侧节点或者右子树中最左侧节点都满足,我们可以选一个节点将待删除节点值替换掉(这里替换成左子树最右侧节点)。
这个点替换之后该怎么办呢?很简单啊,二叉树用递归思路解决问题,再次调用删除函数在左子树中删除替换的节点即可。

这里演示是选取左子树最大节点(最右侧)替代,当然使用右子树最小节点也能满足在这待删除的大小关系,原理一致。整个删除算法流程为:
这部分操作的代码为:
public node remove(int x, node t)// 删除节点 { if (t == null) { return null; } if (x < t.value) { t.left = remove(x, t.left); } else if (x > t.value) { t.right = remove(x, t.right); } else if (t.left != null && t.right != null)// 左右节点均不空 { t.value = findmin(t.right).value;// 找到右侧最小值替代 t.right = remove(t.value, t.right); } else // 左右单空或者左右都空 { if (t.left == null && t.right == null) { t = null; } else if (t.right != null) { t = t.right; } else if (t.left != null) { t = t.left; } return t; } return t; } 完整代码这个完整代码是笔者在大三时候写的,可能有不少疏漏或者不规范的地方,仅供学习参考,如有疏漏错误还请指正。
二叉排序树完整代码为:
package 二叉树; import java.util.ArrayDeque; import java.util.Queue; import java.util.Stack; public class BinarySortTree { class node {// 结点 public int value; public node left; public node right; public node() { } public node(int value) { this.value = value; this.left = null; this.right = null; } public node(int value, node l, node r) { this.value = value; this.left = l; this.right = r; } } node root;// 根 public BinarySortTree() { root = null; } public void makeEmpty()// 变空 { root = null; } public boolean isEmpty()// 查看是否为空 { return root == null; } public node findmin(node t)// 查找最小返回值是node,调用查看结果时需要.value { if (t == null) { return null; } else if (t.left == null) { return t; } else return (findmin(t.left)); } public node findmax(node t)// 查找最大 { if (t == null) { return null; } else if (t.right == null) { return t; } else return (findmax(t.right)); } public boolean isContains(int x)// 是否存在 { node current = root; if (root == null) { return false; } while (current.value != x && current != null) { if (x < current.value) { current = current.left; } if (x > current.value) { current = current.right; } if (current == null) { return false; } // 在里面判断如果超直接返回 } // 如果在这个位置判断是否为空会导致current.value不存在报错 if (current.value == x) { return true; } return false; } public node insert(int x)// 插入 t是root的引用 { node current = root; if (root == null) { root = new node(x); return root; } while (current != null) { if (x < current.value) { if (current.left == null) { return current.left = new node(x);} else current = current.left;} else if (x > current.value) { if (current.right == null) { return current.right = new node(x);} else current = current.right; } } return current;//其中用不到 } public node remove(int x, node t)// 删除节点 { if (t == null) { return null; } if (x < t.value) { t.left = remove(x, t.left); } else if (x > t.value) { t.right = remove(x, t.right); } else if (t.left != null && t.right != null)// 左右节点均不空 { t.value = findmin(t.right).value;// 找到右侧最小值替代 t.right = remove(t.value, t.right); } else // 左右单空或者左右都空 { if (t.left == null && t.right == null) { t = null; } else if (t.right != null) { t = t.right; } else if (t.left != null) { t = t.left; } return t; } return t; } } 结语这里我们学习了解了树、二叉树、以及二叉搜素树,对于二叉搜素树插入查找比较容易理解,但是实现的时候要注意函数参数的引用等等。

