同时我们可以知道,特征值和特征向量有很多个,当λ最大的时候所对应的特征向量,我们把它叫作主成份向量。如果需要将m降维为n,只需要去前n大的特征值所对应的特征向量即可。
方法二:
对于上面二维降成一维的问题来说,找到那个使得方差最大的方向就可以了。不过对于更高维,首先我们希望找到一个方向(基)使得投影后方差最大,当我们找第二个方向(基)的时候,为了最大可能还原多的信息,我们显然不希望第二个方向与第一个方向有重复的信息。这个从向量的角度看,意味这一个向量在另一个向量的投影必须为0.
这就有:
这时候我们思路就很明了:将一组N维向量降为K维(K大于0,小于N),其目标是选择K个单位(模为1)正交基,使得原始数据变换到这组基上后,各字段两两间协方差为0,而字段本身的方差则尽可能大。
还是假设我们原始数据为A

我们做一个处理
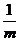
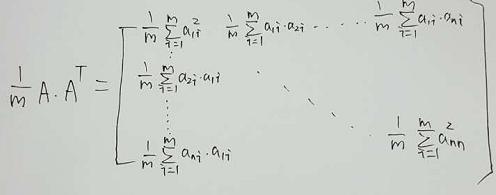
我们发现要是能找到一个基使得这个矩阵变成一个,除了斜对角外,其余全是0的话,那这个基就是我们需要的基。那么问题就转换成矩阵的对角化了。
先说一个先验知识:
在线性代数上,我们可以知道实对称矩阵不同特征值对应的特征向量必然正交。对一个n行n列的实对称矩阵一定可以找到n个单位正交特征向量,设这n个特征向量为e1,e2,⋯,en。
组合成矩阵的形式如图:
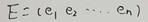
由上结论又有一个新的结论就是,对于实对称矩阵A,它的特征向量矩阵为E,必然满足:
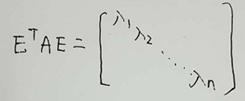
有了这个先验知识,我们假设原始数据A,基为U,投影后的数据为Y。则有Y=UA。根据上面所说的要是投影后的矩阵Y的
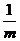
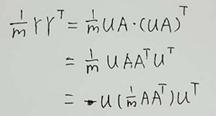
要是
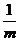
代码实现:
刚才说了两种PCA的计算思路,我们简单看下代码的实现吧,由于matlab自带了求特征向量的函数,这边使用matlab进行模拟。


我们用测试数据试试:

当我们只保留0.5的成分时,newA从3维降到1维,当进行还原时,准确性也会稍微差些
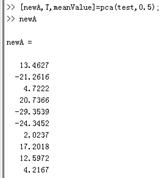
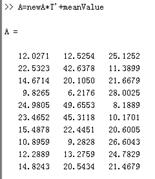
当我们保留0.9的成分时,newA从3维降到2维,当进行还原时,还原度会稍微好些。

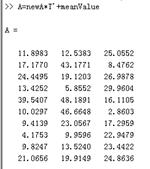
当我们保留0.97的成分时,就无法降维了。这时候就可以100%还原了。

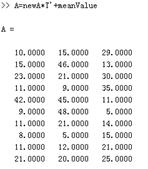
总结一下:

