
这是悟空的第 78 篇原创文章。
本文已收录 Github:https://github.com/Jackson0714/PassJava-Learning
韩信点兵的成语来源淮安民间传说。常与多多益善搭配。寓意越多越好。我们来看下主公刘邦和韩信大将军的对话。
刘邦:“你觉得我可以带兵多少?”
韩信:“最多十万。”
刘邦不解的问:“那你呢?”
韩信自豪地说:“越多越好,多多益善嘛!
假如刘邦现在给了韩信 1000 个士兵,需要大致均匀分成三组。士兵的编号是 6 位数,从 1-100000 随机分配。比如第一个士兵的值是 245,第二个士兵的编号是82593,其他士兵类似。那么如何对士兵进行分配呢?
刘邦:韩将军,你看这些士兵怎么分配好呢?
韩信:这还不简单,我的一技能就能搞定。
一技能:哈希算法 分组韩信的一技能哈希算法:将士兵的编号 num 值当做一个 hash 值,再和总做组数 N 做取余操作,得出的结果在 0 到 N - 1 之间,这个士兵就属于那个组。
如下图所示,每来一个士兵都有一个六位的 hash 值(也可以称作编号),然后被韩信用除以 3 取余数的方式分配到三个组。比如第一组中的编号为 123456 的士兵,除以 3 之后,整除,余数为 0,所以分配到第一组。

现在已经分好组了,假如想找到编号为 666666 的士兵该怎么找?首先将 666666 除以 3,得到余数 0,说明在第一个组,然后去第一个组里面找就可以了。
这里有小伙伴可能会问,为什么不是把所有士兵放到一个组?
因为一个组太大了,影响行军速度。映射到互联网架构中,就是通过增加节点从而减小单节点的负载压力。
哈希分组弊端刘邦看了这个一技能后,大呼:
韩将军真是厉害。
哈希算法看起来很完美,那我再给你五百士兵,需要分成四个组怎么办?
这时,韩信的副将说话了:
这还不简单,再用 4 取余不就好了吗?
刘邦摸着下巴思索片刻后,对副将说:
这个方案可行,但很多士兵都被重新分组了,刚刚建立的团队友情就被分解了。
我们来看下刘邦为什么觉得方案不可行。
比如原来分配到一组的编号为 3 的士兵,当分成四组的时候,通过公式计算:3%4=3,所以会分配到到第四组。
依次类推,会发现很多士兵进行了重新分配,只有小部分不会变换分组,比如 1,2,12 等等。
韩信对着刘邦点点头,对着主公说道:
主公,您说得没错,这就是我的一技能的弱点所在。
不过我还有一个技能:一致性哈希。
二技能:一致性哈希 哈希环一致性哈希算法也用了取模运算,但是它与哈希算法不同的地方:
哈希算法:对节点的数量进行取模运算。
一致性哈希算法:对 2^32 进行取模运算。
可以想象一下,一致性哈希算法,是将整个哈希值空间组成了一个虚拟的圆环,也就是哈希环。
如下图,把 3 个组映射到固定大小为 2^32 的哈希环中。三个组一共将整个环分成了三个区域,C-A(第一组)、A-B(第二组)、B-C(第三组)。如下图所示:

第一组负责存储落在 C-A 区间内的数据。
第二组负责存储落在 A-B 区间内的数据。
第三组负责存储落在 B-C 区间内的数据。
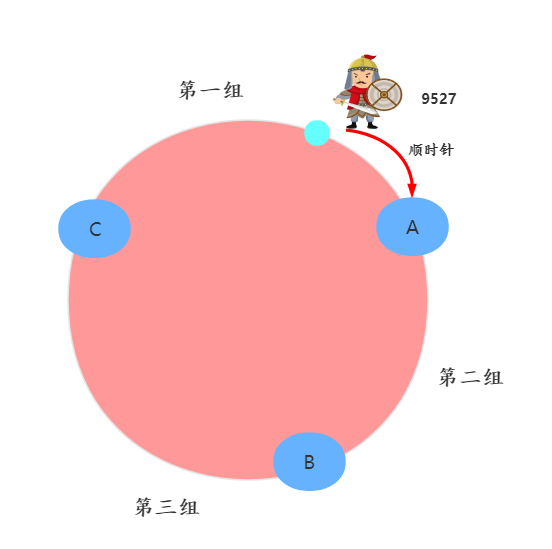
士兵分配假定编号为 9527 的士兵,进行哈希运算后,落到 C-A 区域。如下图所示:

第二步,让这个士兵顺时针往前走,遇到的第一个节点 A 就是他所在的组了。如下图所示:
目前三个节点的时候,假定编号为 89757 的士兵经过哈希运算后,分配到了 B-C 区域(第三组),也就是属于 C 节点管控。如下图所示:

回到刘邦刚问的问题,如果分组变成四组,该怎么进行士兵分配。
如下图所示,增加一个节点 D,原来的区域 B-C 变成了区域 B-D(第三组) 和 D-C(第四组)。


