最近搞Canvas绘图,知道了JavaScript中提供了atan2(y,x)这样一个三角函数。乍眼一看,不认识,毕竟在高中时,学过的三角函数有:sin,cos,arcsin,arccos,tan,arctan等,并没有这个。而工作中又需要用到它,所以这里就做了个简单的了解。
在坐标系中理解tan和atan
回顾一下三角函数tan:
tanθ,用三角函数来表示时,它的值等于sinθ/cosθ,如果将其放到坐标系中,它的的值等价于:dy/dx。在坐标系中,任意两个点所组成的直线,相对于x轴的斜率就是tanθ= dy /dx,相对于y轴的斜率就是dx/dy,此时我们用cot来表示;其中,dy是两个点的y坐标的差值,dx是两个点的x坐标的差值。
那么坐标系内除了y轴,任何一个点(x,y),相对于x轴的斜率就是y-0/x-0,也即是y/x。
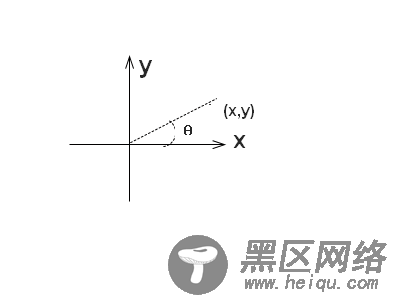
我们将tanθ称为一条直线相对于x轴的斜率,那么θ就是相对于x轴的夹角(旋转角度)了。
tan,是根据角度计算斜率的。那么反过来arctan(反正切)自然就认为是根据斜率来计算角度的。
为何存在atan2 ?
在JavaScript中,提供了两个arctan函数,一个是atan,一个是atan2。atan就是我们所熟知arctan。其实在很多编程语言中都提供了atan2。
那么atan2又是怎么回事呢?
要知道这个,需要知道arctan的不足之处:
arctan的返回值范围是(-π/2, π/2)不包括, ±π/2,也就是(两个点组成的直线与x轴夹角是90°)90°是计算不出来的。为啥呢?在计算arctan ( dy/dx)时,如果两个点(x1,y1),(x2,y2)组成的直线与x轴的夹角呈90°时,dx= x2-x1 = 0,0是不能作为除数的,所以就无法计算这种情形。
值的范围也就是计算的角度的范围在(-π/2, π/2),从坐标系来看,这个角度的范围只能是在第1、4象限,并不能表示出第2、3象限的角。
为了弥补atan的不足,在计算机编程领域,引入了atan2函数,它的计算结果是在(-π,π]。它正好可以覆盖整个坐标系,包括90°的情形。
它的计算过程是怎样的呢?
关于这个,我从wikipedia上摘取了它的计算过程:

atan2的应用
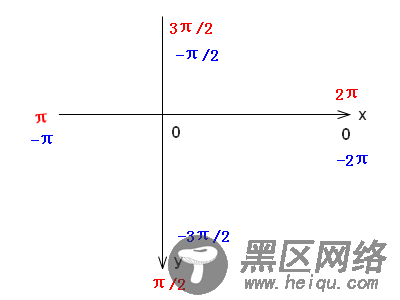
在第一小节中的那张图中的坐标系,是我们熟知的。在HTML、Canvas中,坐标系并不像我们熟知的坐标系那样。它是这样的:
从x轴正向沿顺时针方向,所经过的角度分别是0,π/2,π,3π/2,2π。
从x轴正向沿逆时针方向,所经过的角度分别是0,-π/2, -π,-3π/2,-2π。