我本一介小码农,整日耕于代码中。
一觉醒来竟穿越,略施算法得圣宠。
一每日的生活就好像一遍遍for循环,上班,开会,撕逼,加班,摸鱼,加班摸鱼。
好在,最近可以看《赘婿》,把我从千篇一律的生活中拯救出来。
又是一个周日的晚上,看着主人公在古代入赘豪门,广开分铺,结识丞相,不禁感慨我要是能穿越就好了,可是一个程序员穿越回去可以干什么呢?
郁闷之下开了一瓶啤酒,边胡思乱想边追剧,不胜酒力的我就这么迷迷糊糊睡着了。
不知道过了多久,我耳边听见有人在喊:"大人大人,皇上有急事招您!"
我惊醒一看,周围已不是我出租屋的装饰,而且立着汉白玉的柱子,四周的墙壁也全是白色石砖雕砌而成。
我一把拿过床边的镜子,镜子中的人留着长发,貌比潘安,散发着一股年少有为不自卑的气质,一扫往日一副郁郁不得志状态。
我竟然真的穿越了!
二为了保证穿越之后的仪式感,我还是打了自己两巴掌,没有问题!
门外的仆人越发着急,我忙说起来了起来了,心想我都位高权重了咋刚起床就得上班。
仆人直接进来帮我换好衣服,并说高公公在外面等候多时了。
在高公公的带领之下,我们坐上马车直奔皇宫。
担心言多必失,我全程不发一言。但是依然按捺不住我激动的心情,这次投胎我给自己打个满分。
很快到了皇宫,高公公带着我一路小跑,直奔皇上书房。
行过电视剧看过的大礼之后,皇上满脸愁容,叹气道;"爱卿啊,贵妃整日郁郁寡欢,问起原因,是因为思念家乡的荔枝了,可蜀中到长安数千里,中间涉及了几百条官道,途经几百个驿站,绕来绕去,送到时荔枝都已腐烂。爱卿可有什么法子,来找出蜀中到长安的最近道路啊。"
我一听,这不是我的老本行吗,无向图的最短路径啊!
我当时恨不得表演一下宣纸毛笔写算法的祖传手艺,可一寻思,皇帝也看不懂代码,搞不好以为我在鬼画符。
算了,能和皇帝讲清楚就行了。
于是我上前一步:"臣有一计,按此计可寻得最短路径,定可让贵妃吃上鲜美荔枝。"
皇上大喜:"笔墨伺候,让爱卿给朕道来。"
我在纸上画到
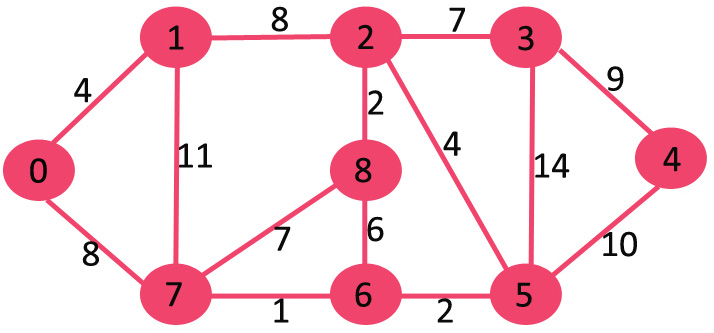
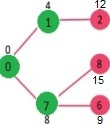
皇上请看,我们可以类比于从0点到4点的最短距离。
算法很简单,用三个变量,重复走三步,即可得到最终结果。
三个变量sptSet (shortest path tree set) 数组
创建一个数组sptSet,用来记录最短路径中包含的顶点,也就是哪个顶点计算出来到源点的最近距离了,就把它加进去。
最初,此集合为空。
distance数组
创建一个数组记录每个顶点到源点的距离,当然最开始为INFINITE(无限大)。
同时将源顶点的距离值指定为0。
parent数组
这个是当我们更新distance数组的时候,记录该节点的上一个节点,好记录整个最短路径所通过的节点。
三步走
选出一个不在sptSet数组并且distance数组中之最小的节点,该节点我们可以称之为u。
当然,第一次就是选择源节点0。
把u放到sptSet数组中。
遍历u所有相邻的顶点,如果相邻顶点i的距离值(即distance[i]的值)大于u的距离值加上u到该相邻顶点的距离之和S,我们更新相邻顶点的距离值为S。
同时,修改parent数组,即parent[i]=u。
如此重复下去,直到我们遍历完全部节点,就可以获取源点到每一个节点的最短路径。
当然,从蜀中到长安的最短路径也知晓了。"
皇上一脸茫然的看着我,我才意识到,我已经穿越了,这样讲皇上肯定听不懂,就是看这个文章的现代人都不一定能懂。
不如一步步推导,皇上肯定更加清晰。
我又说道:"皇上,来我们实际走一遍,您便一目了然。"
数组
sptSet最初为空,distance为{0,INF,INF,INF,INF,INF,INF,INF},其中INF表示无穷大。 现在选择距离最小的顶点,也就是选择顶点0,将其包含在sptSet中。
因此,sptSet变为{0}。 将0包含到sptSet之后(图中变绿节点),更新其相邻顶点的距离值。
0的相邻顶点是1和7,1和7的距离值更新为4和8。
同时修改parent数组
parent[1] = 0 parent[7]=0
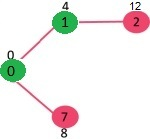
选择当前具有最小距离值且尚未包含在sptSet中的顶点,这次选择了顶点1并将其添加到sptSet。 因此,sptSet现在变为{0,1}。
更新相邻顶点的距离值,因此顶点2的距离值变为12。
同时修改
parent[2]=1