然而,当预测 GBB 远离真实 GBB 距离时, L1 损失函数的值接近于 1 ,训练过程产生梯度小且收敛速度慢。 L2 损失函数避免了上述问题,但与 IoU 的几何关系弱,因此,建议首先采用 L2 损失函数训练,然后切换至 L1 损失函数。
2.3 ProbIoU 的特性基于 Hellinger Distance 的 ProbIoU 具有以下特性:
三个函数中所有参数都是可微的;
Helinger Distance 满足所有距离度量标准 ;
损失函数对对象缩放是不变的。
3. 实验结果 3.1 不同检测框 实验结果在 COCO2017 上进行训练, 通过对比 GBB 、OBB 、HBB 检测得到的 IoU,可得到如下结论:
GBB 在 COCO 2017 中 77 类别的均值 IoU 要高于 HBB 和 OBB
GBB 在 traffic light 、 microwave 、 tv 三个类别要差于 HBB 和 OBB
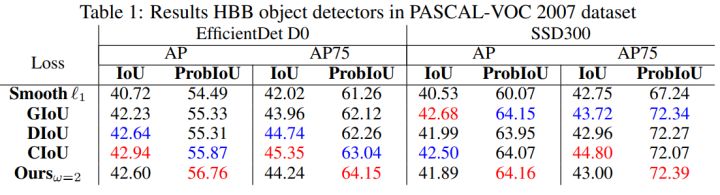
3.2 ProbIoU loss 对于 HBB 、 OBB 检测的提升将基于 ProbIoU 的损失函数用于 HBB 检测任务中, 分别采用 EfficientDet D0 和 SSD 300 在 PASCAL-VOC 2007 数据集训练。如下表所示, 相对于 IoU , 采用 ProbIoU 方法 在 AP 及 AP75 均有提升,采用基于 ProbIoU 的损失函数的模型均能达到较高 AP 。
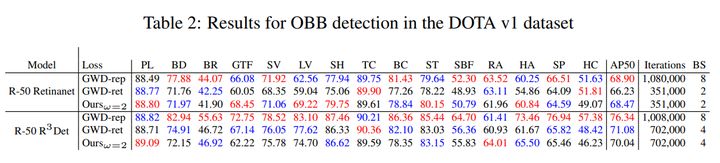
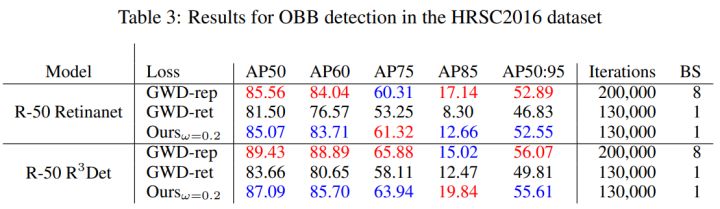
将基于 ProbIoU 的损失函数用于OBB 检测任务中, 分别采用 R-50 Retinanet 及 R-50 R3Det ,在 DOTA v1 及 HRSC2016 数据集进行训练。如下表所示,在 DOTA V1 数据集,采用 Retinanet 模型时,基于 ProbIoU 的 损失函数 AP 比 GWP-ret 高 2%;采用 R3Det 模型时, 其结果与GWD-rep 和GWD-ret 接近。在 HRSC2016 数据集上,基于 ProbIoU 的损失函数结果与GWD-rep 相当, 并且优于GWD-ret 。
本文所呈现的方法包含以下三个重要部分 :
采用高斯分布形式检测框 (GBB)
提出基于 Hellinger Distance 的 ProbIoU,并提出对应的损失函数 L1,L2
训练过程中,采用L1 和 L2 损失函数组合效果更佳

