梯度下降法的三种形式BGD、SGD以及MBGD

在应用机器学习算法时，我们通常采用梯度下降法来对采用的算法进行训练。其实，常用的梯度下降法还具体包含有三种不同的形式，它们也各自有着不同的优缺点。

下面我们以线性回归算法来对三种梯度下降法进行比较。

一般线性回归函数的假设函数为：

对应的损失函数为：

（这里的1/2是为了后面求导计算方便）
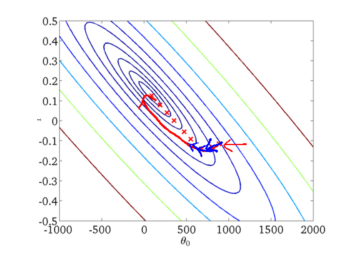
下图作为一个二维参数（

，

）组对应能量函数的可视化图：

下面我们来分别讲解三种梯度下降法

批量梯度下降法BGD

我们的目的是要误差函数尽可能的小，即求解weights使误差函数尽可能小。首先，我们随机初始化weigths，然后不断反复的更新weights使得误差函数减小，直到满足要求时停止。这里更新算法我们选择梯度下降算法，利用初始化的weights并且反复更新weights：

这里

代表学习率，表示每次向着J最陡峭的方向迈步的大小。为了更新weights，我们需要求出函数J的偏导数。首先当我们只有一个数据点（x,y）的时候，J的偏导数是：

则对所有数据点，上述损失函数的偏导（累和）为：

再最小化损失函数的过程中，需要不断反复的更新weights使得误差函数减小，更新过程如下：

那么好了，每次参数更新的伪代码如下：

由上图更新公式我们就可以看到，我们每一次的参数更新都用到了所有的训练数据（比如有m个，就用到了m个），如果训练数据非常多的话，是非常耗时的。

下面给出批梯度下降的收敛图：

从图中，我们可以得到BGD迭代的次数相对较少。

随机梯度下降法SGD

由于批梯度下降每跟新一个参数的时候，要用到所有的样本数，所以训练速度会随着样本数量的增加而变得非常缓慢。随机梯度下降正是为了解决这个办法而提出的。它是利用每个样本的损失函数对θ求偏导得到对应的梯度，来更新θ：

更新过程如下：