基于《算法》一书的红黑树的插入和删除。看过不同的教材,也有不同的实现方式,但是最终的结果也大致相同,感觉这个比较容易理解,就采用这种的方式来进行简单实现。 # 定义树节点的实体类型 ```java private static final boolean RED = true; private static final boolean BLACK = false; /** * 红黑树的节点结构 * 保存的值,左节点,右节点以及颜色(true为红色,false为黑色) * 默认添加一个红节点 * * @param */ static final class RedBlackTreeNode> { E val; RedBlackTreeNode left; RedBlackTreeNode right; boolean color = RED; RedBlackTreeNode(E val) { this.val = val; } } ``` 这里简单的定义了一下红黑树,并且只有节点,并不是map这样的k-v结构。如果定义k-v结构到时比较的时候比较k即可。 用了泛型,并且要支持比较(继承自Comparable),不然无法比较大小进行插入。 然后定义了一个值,左节点和右节点,然后颜色默认为红色。 再增加一个构造函数即可 # 定义公共方法 主要做的就是插入和删除节点,为了方便查看是否符合添加了一个中序遍历的打印方法 ```java public class RedBlackTree> { RedBlackTreeNode head; public void add(E e) { ... } public void remove(E e){ ... } public void printTree(){ ... } } ``` 定义这些公共方法来对外部调用,具体实现可以放到私有方法中。 # 变换操作 在红黑树的变换中主要有三个:左旋,右旋,变色。接下来我们就来实现这三个方法。 **旋转操作可以保持红黑树的两个重要性质:有序性和完美平衡性** ## 左旋 ```java private RedBlackTreeNode rotateLeft(RedBlackTreeNode node) { //变换位置 RedBlackTreeNode result = node.right; node.right = result.left; result.left = node; //换色 result.color = node.color; node.color = RED; return result; } ``` **当右节点为红色, 左节点为空或者黑色时,需要进行左旋操作。** 首先定义一个变量存储右节点,然后将右节点的左节点作为父节点(传入参数)的右节点。这时与右节点(定义的变量)断开了关联。 然后将定义的变量(右节点)的左节点设置为参数节点(左节点之前已经赋值到参数节点的右节点上)。 还需进行一步换色,将定义变量的颜色设置为父节点的颜色(不影响上一级的操作),然后将父节点设置为红色。 将定义的变量作为父节点返回。 ## 右旋 ```java private RedBlackTreeNode rotateRight(RedBlackTreeNode node) { //变换位置 RedBlackTreeNode result = node.left; node.left = result.right; result.right = node; //变色 result.color = node.color; node.color = RED; return result; } ``` **当左节点为红色,左节点的左节点也为红色时,需要进行右旋操作。** 这个与左旋基本类似,将左节点作为父节点返回,然后对其他节点也要确保不丢失,还有换色操作不能影响红黑树的特性。 ## 换色 ```java private void flipColor(RedBlackTreeNode node) { node.left.color = BLACK; node.right.color = BLACK; node.color = RED; } ``` **当两个子节点都为红色时,需要进行换色** 让两个子节点变为黑色,父节点变为红色 # 完成公共方法的实现 刚才我们在上面有提到,需要判断节点的颜色,虽然我们在节点的类型中定义了`color`属性,但是考虑到其他情况还是写一个方法来完成判断颜色的功能: ## isRed(Node) ```java private boolean isRed(RedBlackTreeNode node) { if (node == null) { return false; } return node.color; } ``` 当节点为空时返回false即为黑色,不然判断节点的color属性是否为红色。 还有一个中序打印的方法 ## printTree() ```java public void printTree() { print(head); } private void print(RedBlackTreeNode node) { if (node == null) { return; } print(node.left); System.out.print(node.val + " "); print(node.right); } ``` 在对外部的方法中调用了内部方法,传入了头结点。 由于是中序遍历,所以需要先遍历左节点,然后打印自己,然后遍历右节点。这是一个递归操作,所以需要定义终止条件:当节点为空时就返回。 # 具体实现 # add() ```java public void add(E val) throws IllegalAccessException { if (val == null) { throw new IllegalAccessException("不能添加null值"); } head = addVal(val, head); //最终将根节点设置为黑色 head.color = BLACK; } private RedBlackTreeNode addVal(E val, RedBlackTreeNode node) { //达到最终的节点,如果为空则新建一个红色的节点 if (node == null) { return new RedBlackTreeNode(val); } if (val.compareTo(node.val) 0) { //如果大,则右节点为 新建节点后返回的节点(可能会经过调整) node.right = addVal(val, node.right); } else { //值相等 return node; } //判断平衡等操作 if (isRed(node.right) && !isRed(node.left)) { //右节点为红色,左节点为空或者黑色时需要进行左旋 node = rotateLeft(node); } if (isRed(node.left) && isRed(node.left.left)) { //左节点为红色,左节点的左节点也为红色时,需要进行右旋 node = rotateRight(node); } if (isRed(node.left) && isRed(node.right)) { //当两个子节点都为红色时,需要进行变色 flipColor(node); } return node; } ``` 在公共方法中首先进行了一个参数校验,如果为空则无法比较所以就抛出一个异常。 然后调用私有方法进行添加节点:传入的参数为要添加的值,树的头结点。 在私有方法中首先判断了传入的节点是否为空,如果为空则新建一个红色节点返回。 当不为空时进行大小判断,判断是添加在左子树还是右子树上,然后递归调用当前方法,传入要添加的值和左节点或右节点,如果相等则直接返回当期节点即可(不是map不用重新改变value)。并且添加后可能会进行调整,所以需要重新赋值。 接下来就是判断是否符合红黑树的规定,然后进行左旋,右旋,变色等操作。这时也会进行重新调整,所以需要重新赋值。 操作完成后返回到公共方法中。 在公共方法中将头结点的颜色设置为黑色,保证红黑树的特性。 ## remove() ```java public void remove(E val) throws IllegalAccessException { if (val == null) { throw new IllegalAccessException("不允许null值操作"); } if (head == null) { throw new IllegalAccessException("树为空"); } head = removeVal(val, head); } private RedBlackTreeNode removeVal(E val, RedBlackTreeNode node) throws IllegalAccessException { if (node == null) { throw new IllegalAccessException("val not exist!"); } if (val.compareTo(node.val) 0) { node.right = removeVal(val, node.right); } else { if (node.right != null) { node = getRightMinNode(node); } else if (node.left != null) { node = getLeftMaxNode(node); } else { node = null; } } //判断平衡等操作 if (node != null) { //判断平衡等操作 if (isRed(node.right) && !isRed(node.left)) { //右节点为红色,左节点为空或者黑色时需要进行左旋 node = rotateLeft(node); } if (isRed(node.left) && isRed(node.left.left)) { //左节点为红色,左节点的左节点也为红色时,需要进行右旋 node = rotateRight(node); } if (isRed(node.left) && isRed(node.right)) { //当两个子节点都为红色时,需要进行变色 flipColor(node); } } return node; } ``` 在公共方法中进行参数校验,如果删除的是null,则抛出异常。 然后当树为空时也不能进行删除操作。删除操作也可能会进行结构修改,所以也需要进行重新赋值。 用参数与当前节点比较,如果小则递归传入左节点,如果大则递归传入右节点,当节点为空时表示要删除的节点不再树中,我在这里是抛出了异常,可能有些不太妥当。 如果与当前节点相同,则删除当前节点。这时就暴露了一个问题,当当前节点有子节点时如果进行删除。其实这也分为几种情况即上面代码中的第20-26行: 1. 当前节点无子节点,删除当前节点即置为null即可。 2. 将右子节点的最小节点作为当前节点的替代,然后删除这个最小节点。 ```java /** * 获取右侧树的最小节点 * * @param node * @return */ private RedBlackTreeNode getRightMinNode(RedBlackTreeNode node) { RedBlackTreeNode parent = node.right; if (parent.left == null) { node.right = parent.right; return parent; } RedBlackTreeNode result = parent.left; //可能有优化的地方 while (result.left != null) { parent = parent.left; result = parent.left; } parent.left = null; return result; } ``` 3. 当右节点为空时,找到左节点的最大值作为当前节点的替代,然后删除这个最大节点。 ```java private RedBlackTreeNode getLeftMaxNode(RedBlackTreeNode node) { RedBlackTreeNode parent = node.left; if (parent.right == null) { node.right = parent.left; return parent; } RedBlackTreeNode result = parent.right; while (result.right != null) { parent = parent.right; result = parent.right; } parent.right = null; return result; } ``` 进行替换后,需要检查是否符合红黑树的特性是否需要左旋,右旋,变色等操作。 # 验证 ```java public static void main(String[] args) throws IllegalAccessException { RedBlackTree redBlackTree = new RedBlackTree(); redBlackTree.add(1); redBlackTree.add(3); redBlackTree.add(5); redBlackTree.add(7); redBlackTree.add(9); redBlackTree.add(2); redBlackTree.add(4); redBlackTree.printTree(); System.out.println(); redBlackTree.remove(2); redBlackTree.printTree(); System.out.println(); redBlackTree.remove(11); } ``` 首先我们依次添加[1,3,5,7,9,2,4]。然后将树打印,按照预期结果打印出的结果应该是顺序的1~9。然后我们删除2节点,如果我们将插入过程画出来会发现如果删除2,则会造成1,3两个红节点的连接,这不符合红黑树的规定,所以需要进行调整。然后再次进行打印查看结果是否为有误。 最后我们删除一个不存在的值,看它是否会报错。 ```java 1 2 3 4 5 7 9 1 3 4 5 7 9 Exception in thread "main" java.lang.IllegalAccessException: val not exist! at RedBlackTree.removeVal(RedBlackTree.java:33) at RedBlackTree.removeVal(RedBlackTree.java:38) at RedBlackTree.removeVal(RedBlackTree.java:38) at RedBlackTree.removeVal(RedBlackTree.java:38) at RedBlackTree.remove(RedBlackTree.java:28) at Test.main(Test.java:21) ``` 通过输出可以看出结果符合我们的要求,然后也可以通过debug的方法查看删除2节点后的节点情况发现与在草稿上手画版一致。 给出一个刚才插入的图画过程。 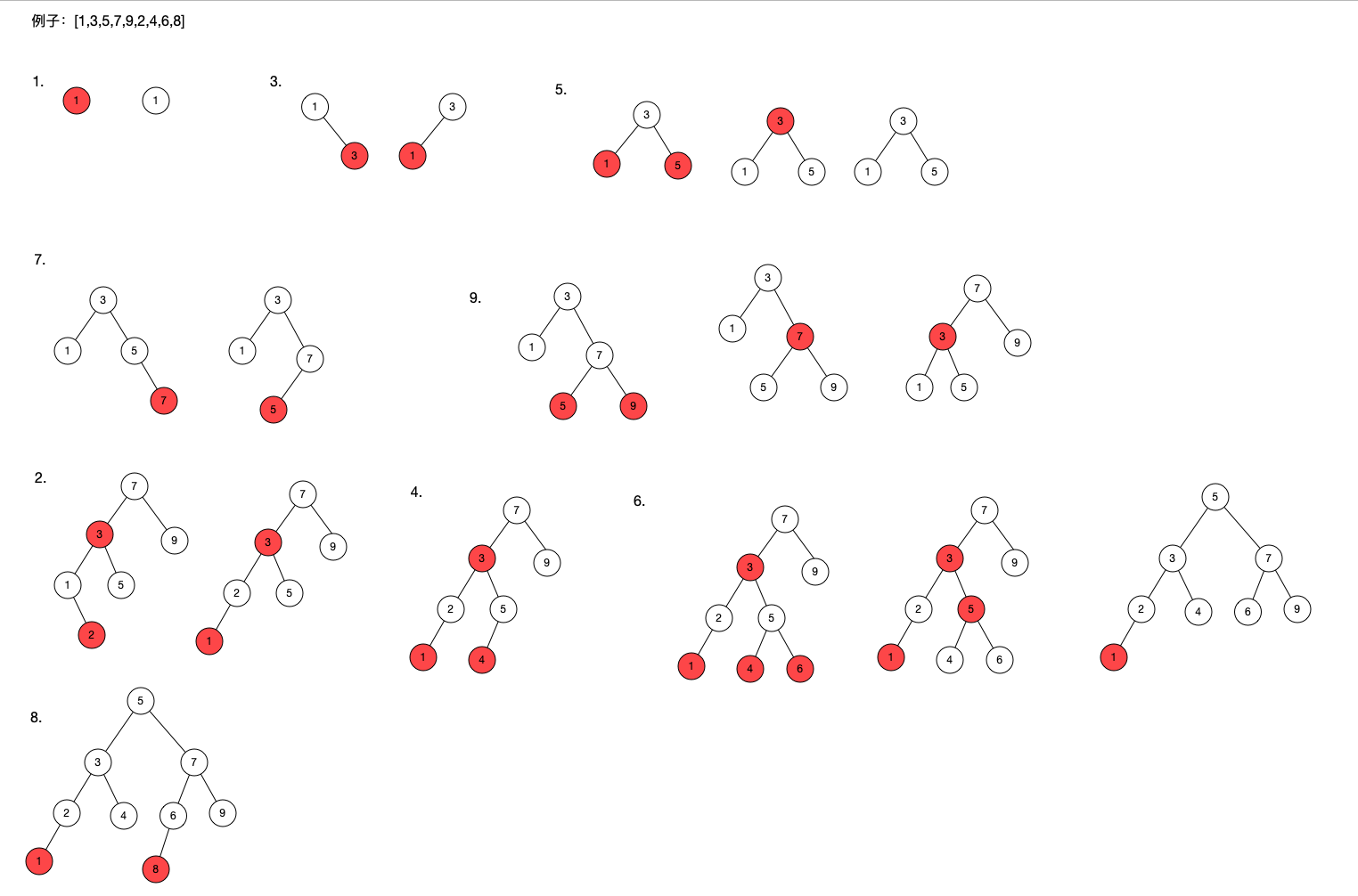 删除2节点后的情况 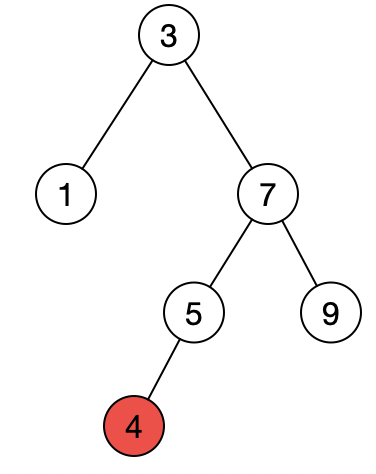 > 本文由博客一文多发平台 [OpenWrite](https://openwrite.cn?from=article_bottom) 发布! 博主邮箱:liunaijie1996@163.com,有问题可以邮箱交流。
手写红黑树的简单实现
内容版权声明:除非注明,否则皆为本站原创文章。

