游戏现在似乎已经成为了大家绕不开的一个娱乐方式,从大型端游到手游,到页游,再到各种 APP 里面的 H5 小游戏,它以各种方式入侵了我们的生活。那么在享受游戏的同时,作为一名前端开发,也开始思考如何开发一款游戏,在技术层面它应当具备什么?
除了基本的游戏画面、动效开发、渲染功能,还有一项值得探究的东西,那就是物理引擎。一个好的物理引擎,保证了游戏内的交互体验和现实中相似,给人提供了更优质的体验。
现在好用的物理引擎有很多,大部分都是开箱即用,但物理引擎的基础和底层逻辑是什么样子的,可能有些人并不了解。从这期开始我们将分多个部分介绍物理引擎的基础,让大家对此更加了解。以下的内容部分参考自《游戏物理引擎开发》。
何为引擎引擎是什么?当然这里是延展了汽车中引擎的概念。在汽车中,引擎——一种能量转换的装置,将其他能变为机械能提供给汽车,是汽车能够运动的核心模块。
那对应的,在开发当中的引擎是什么呢?在我的理解中,是一个可以将一个个功能快速加入到项目中,并且保证功能运转的核心模块。渲染引擎,就能够快速实现内容的渲染。游戏引擎,就能够快速实现一个游戏的基础开发。而物理引擎,就是可以快速模拟现实中物理状态。
了解完引擎是什么之后,我们可以再来关注一下,引擎有什么特点。引擎最大的特点就是两个——快速,通用。它能够快速实现需要的功能,并且有很强的通用性,它并非是针对某个专门的业务开发的,而是针对一大类情况进行开发,所以必须拥有强大的通用性。
快速意味着需要做到功能完善,API 封装完整,使用便捷。通用意味着代码本身的逻辑需要足够底层,应用最基本的逻辑才能做到最大的通用性。
物理引擎的基础一个物理引擎的基础是什么呢?那就是物理和数学。其实一个物理系统在游戏中的体现是整个物理系统内各个对象的位置。每一帧都需要计算物体的位置,使得他们能出现在正确的地方。所以符合物理学规律的数学运算,是一个物理引擎的基础。我们下面的一切都是以此为依据来进行阐述的。
代码中的数学首先要看一下,在游戏世界中,数学在哪些地方起到了作用。无论是在二维还是三维的世界中,针对对象的位置的描述都是由向量来完成的。而向量的处理,免不了的就是向量本身的一些分解、加减、点积、向量积等知识。
所以我们要先建立一个最基础的向量类:
class Vector { x: number y: number z: number constructor(x: number,y: number,z: number) { this.x = x this.y = y this.z = z } setX(x: number) { this.x = x } setY(y: number) { this.y = y } setZ(z: number) { this.z = z } }向量的分解,应用的是三角函数的内容,将一个向量通过角度分解到 x 轴、y 轴、z 轴,或者根据不同轴上的坐标来计算对应的角度。
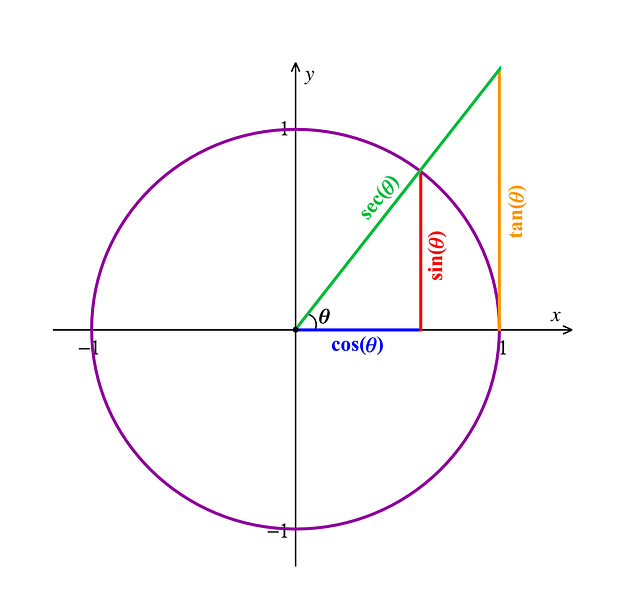
三角函数
而向量的计算原理,就不仔细阐述了。在游戏世界中,最后都会被分解到对应坐标轴的方向进行计算,即便是点积或者向量积也不例外。所以只要熟练运用三角函数和向量计算公式,就能够进行向量的处理了。
我们将给向量增加以下计算方法:
class VectorOperation { add (vectorA: Vector, vectorB: Vector) { // 向量相加 return new Vector( vectorA.x + vectorB.x, vectorA.y + vectorB.y, vectorA.z + vectorB.z ) } minus (vectorA: Vector, vectorB: Vector) { // 向量相减 return new Vector( vectorA.x - vectorB.x, vectorA.y - vectorB.y, vectorA.z - vectorB.z ) } multiply (vectorA: Vector, times: number) { // 向量缩放 return new Vector( vectorA.x * times, vectorA.y * times, vectorA.z * times ) } dotProduct (vectorA: Vector, vectorB: Vector) { // 向量点积 return vectorA.x* vectorB.x + vectorA.y* vectorB.y + vectorA.z* vectorB.z } vectorProduct (vectorA: Vector, vectorB: Vector) { // 向量外积 return new Vector( vectorA.y * vectorB.z - vectorA.z * vectorB.y, vectorA.z * vectorB.x - vectorA.x * vectorB.z, vectorA.x * vectorB.y - vectorA.y * vectorB.x, ) } }而在游戏物理学中,还需要用到一门很重要的数学知识,那就是微积分。
这么说大家可能体会不到,都是一些基础的物理内容,为什么会用到微分和积分呢?来举个例子,先看看最基本的速度公式,先从平均速度开始,是经过的路程除以经过的时间:
$$ v = \frac {s_{1} - s_{0}}{t_{1} - t_{0}} \tag{平均速度}$$

