大家好,我们今天来看一道非常非常经典的算法题——最近点对问题。
这个问题经常在各种面试当中出现,难度不低,很少有人能答上来。说实话,我也被问过,因为毫无准备,所以也没有答上来。是的,这道题有点神奇,没有准备的人往往答不上来。
题意我们先来看下题意吧,题意很简单,在一个平面当中分布着n个点。现在我们知道这n个点的坐标,要求找出这n个点当中距离最近的两个点的间距。

我不确定这个问题是否出自于天文学,但是把它放到天文的背景当中非常合适。想象一下在浩瀚的宇宙当中,存在着无数的星辰,我们想要找到其中距离最近的两颗天体。它们有可能是双子星,也有可能是伴星系……这么想想,有没有觉得很浪漫?
我们来分析一下问题,会发现一个矛盾之处。矛盾的地方在于如果我们要求出每两个点之间的距离,那么复杂度一定是
我当时在面试的时候就是这么回答的,虽然我们现在知道这个说法是错的,但是如果没有这一层信息,你还能判断吗?
分治法如果我们仔细思考一下,会发现这个问题和排序其实非常类似。因为我们在排序的时候,表面上来看每两个点之间都存在大小关系,我们要排序似乎也要获得这些关系。但实际上,我们都知道,无论是快速排序还是归并排序都可以做到
无论是快速排序还是归并排序,本质上都是利用的分治法。那么这道题是否也可以使用分治法求解呢?
答案当然是可以的,既然是使用分治法,那么我们首先要做的就是拆分,将整个的数据拆成两个部分,使用递归分别完成两个部分,然后再合并得到完整的结果。在这个问题当中,我们要拆分数据非常简单,只需要按照x轴坐标对所有点进行排序,然后选择中点进行分割即可,分割之后我们得到的结果如下:
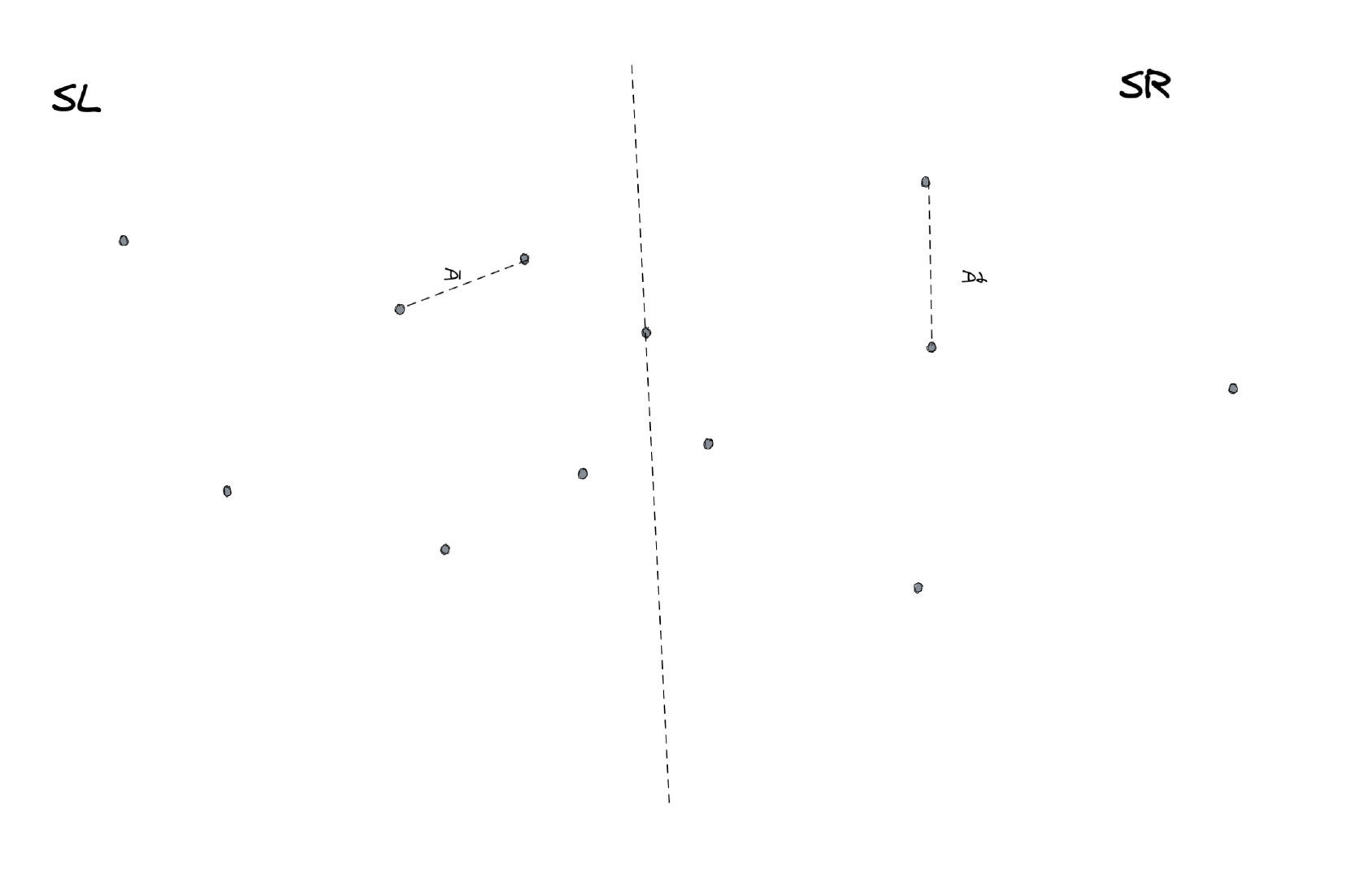
拆分结束之后,我们只需要分别统计左边部分的最近点对、右边部分的最近点对,以及一个点在左边一个点在右边的最近点对即可。对于前面两种情况都很好解决,我们只需要递归就可以搞定了,但对于第三种情况应该怎么办?这也是本题的难点所在。
要分析清楚这个问题不是非常容易,需要深入的思考,首先我们通过递归调用可以获得左边部分SL的最短距离D1以及右边部分SR的最短距离D2。我们取
求出了D之后,我们就可以用它来限定一个点在SL一个点在SR这种情况的点对的范围了,不然的话我们要比较两边各有n/2个点的情况,依然计算复杂度很大。
我们来分析一下问题,我们在左侧随便选择一个点p,我们来想一个问题,对于点p而言,SR一侧所有的点都有可能与它构成最近点对吗?当然不是,有一些离得远的是明显不可能的,对于这些点我们没有必要一一遍历,直接都可以批量忽略。要想和p点构成最近点对,必须在下图这个虚线框起来的范围内。
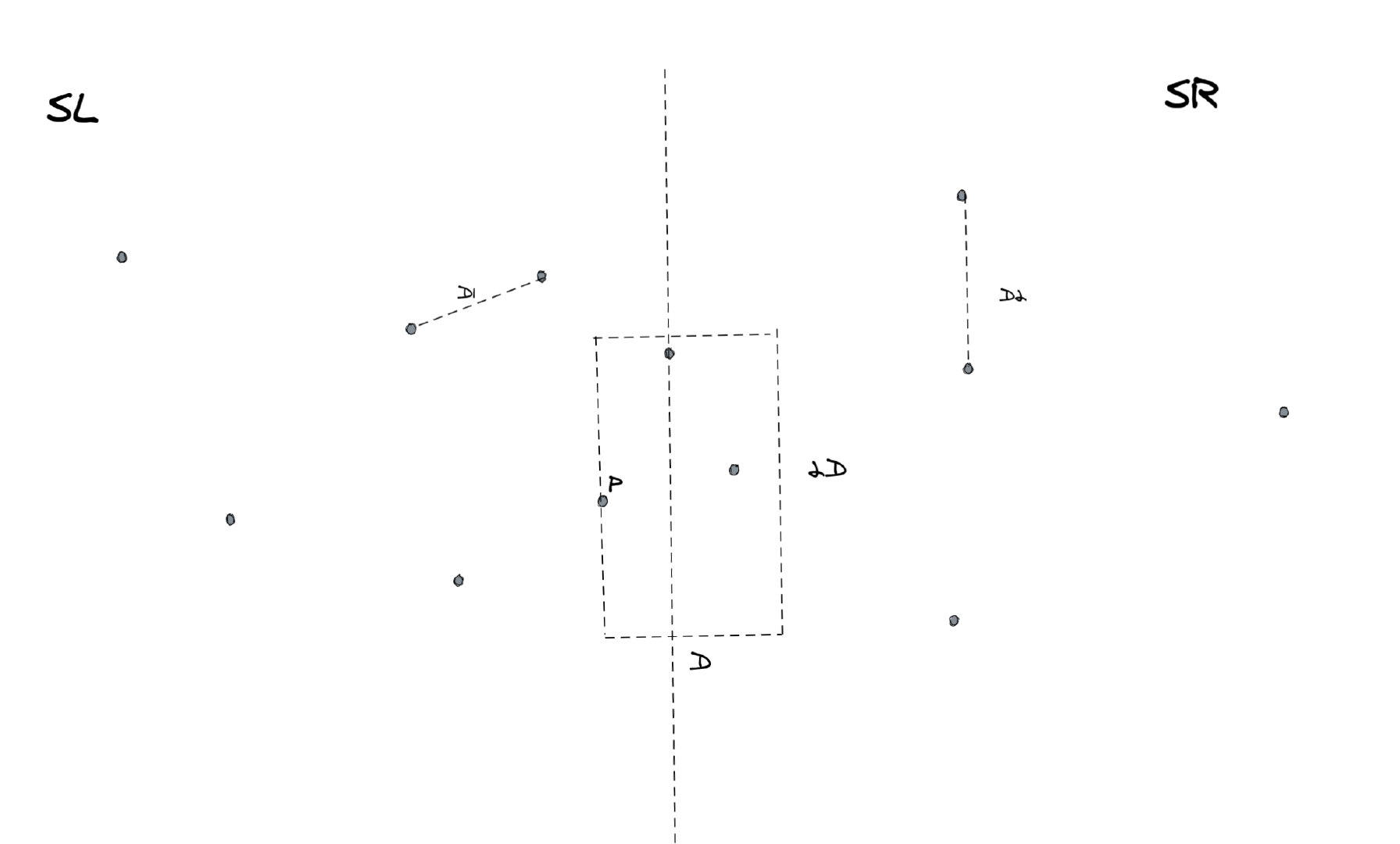
这个虚线构成的框是一个长方形,它的宽是D,长是2D。这是怎么来的呢?其实很简单,对于p点来说,要想和他构成全局的最近点对,那么距离它的距离一定要小于目前的最优解D。既然距离要小于D,那么意味着它们的横纵坐标之差的绝对值必须也要小于D。
当然这个框只是我们直观看到的,在实际算法运行的时候是没有这个框的,我们只能根据坐标轴自己去进行判断某个点在不在框里。
有了这个框之后,我们产生了另外一个问题,那就是这个框到底可以起到多大的作用呢?有了这个框就可以降低算法复杂度了吗?会不会出现右侧所有点都在框里的极端情况呢?
其实我们只需要简单分析一下就会发现这是不可能的,不仅可以判断出这是不可能的,而且我们还可以得出另外一个非常非常惊人的结论。
首先,我们来论证一下为什么右侧所有的点都落在这个虚线框里是不可能的。我们先来看最极端的情况,最极端的情况就是我们选中的p点就在分割线上。那么以它画出来的框应该全部都落在SR区域,画成图大概是这样的:
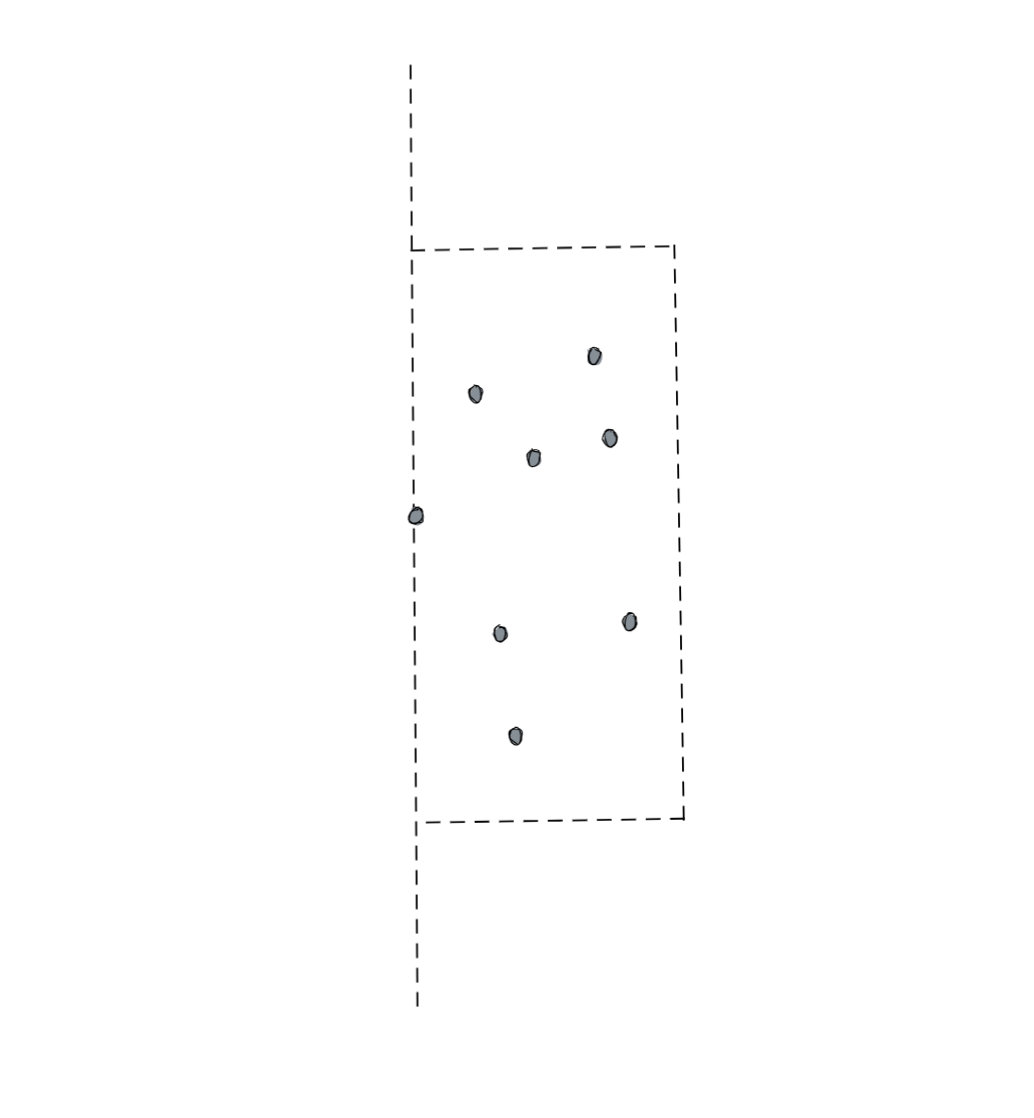
但是我们简单想一下会发现一个问题,就是这个虚线框里的点的数量不可能是无限的。因为对于框里的点我们有一个基本的要求,就是在这个框里并且在SR区域内的点,两两之间的距离不得小于D。如果小于D了就和我们刚才得到D是左右两侧最小距离的结论矛盾了。那么上面图中的情况其实是不可能的,因为这么多点聚集在一起明显存在两个点的距离小于D了,这就矛盾了。
也就是说由于存在这个距离的限制,能够落在这个虚线框里的点的数量是有限的,而且这个数量比大家想的也许要小得多,有多小呢?小到最多只有6个,也就是下面这种情况:
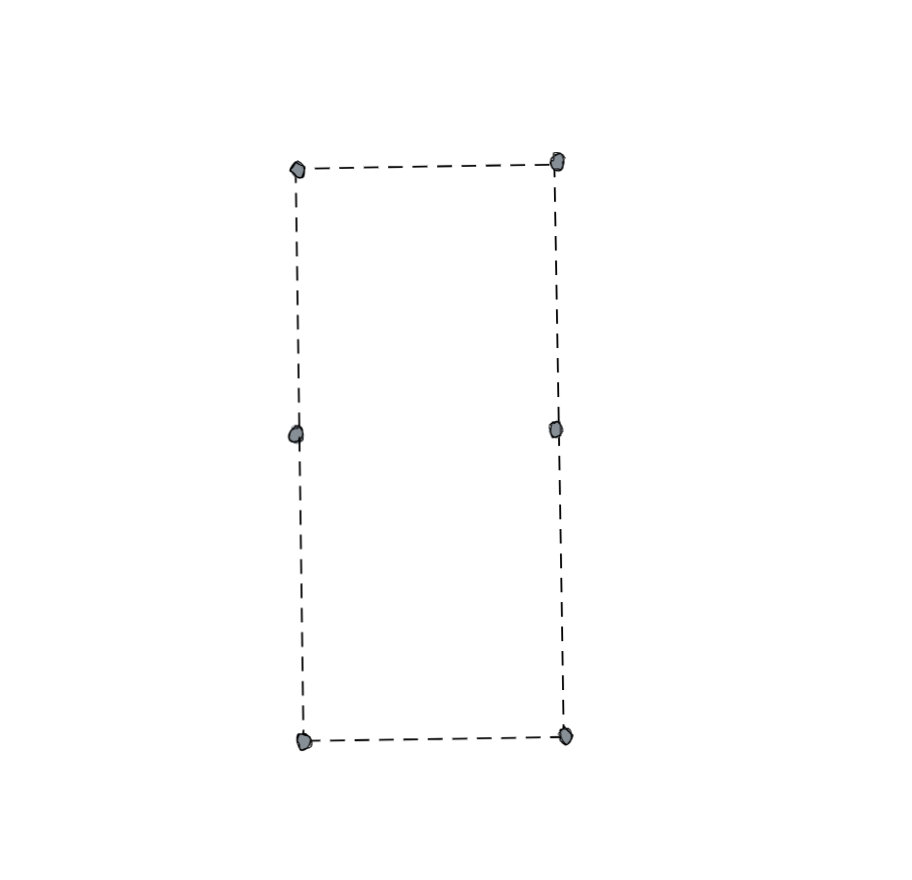
在上图当中,一共有6个点,这6个点两两之间的最短距离是D,这是最极端的情况。无论我们如何往其中加入点,都一定会产生两个点之间的距离小于D。这是我们很直观的感受,有没有办法证明呢?其实也是有的,我们可以把这个矩形进行六等分变成下图这样:
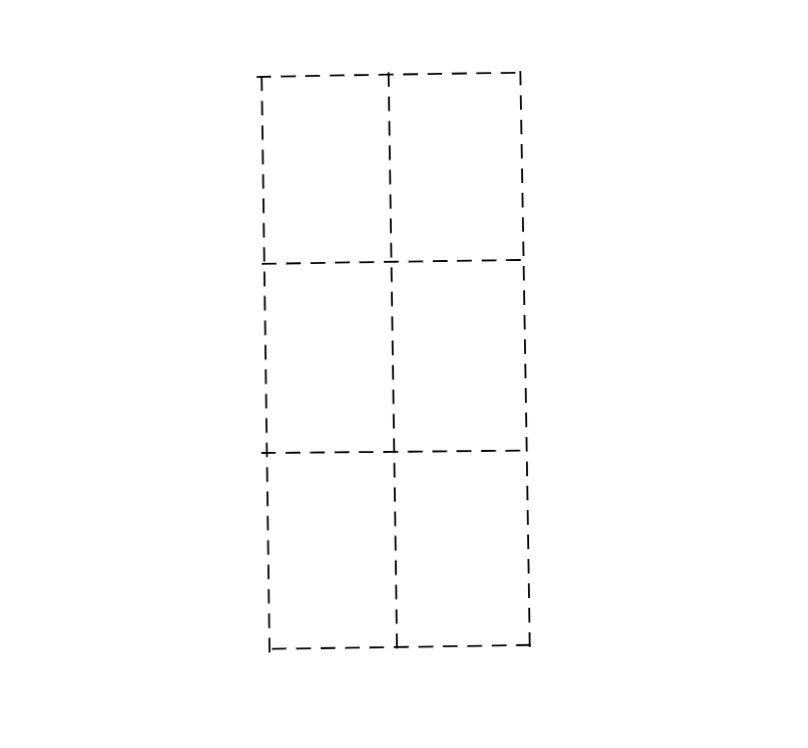
我们来分析一下,上图的每一个小矩形的长是
也就是说对于SL侧的点p,我们在SR侧最多只能找出6个点来可能构成最短点对,这样我们需要筛查的点对数量就大大减小。并且对于SL侧的点来说,并不是所有的点都需要考虑的,只有和中点O横坐标差值小于D的点才需要考虑。
表面上看起来我们所有的分析都结束了,但实际上还有一个问题没有解决。就是我们怎么样找到这6个点呢?显然只根据横坐标是不行的,这个时候就需要考虑纵坐标了。我们将点集分成左右两个部分之后,对右侧部分按照纵坐标进行排序,对于左侧的点(x, y)而言,我们只需要筛选出右侧满足纵坐标范围在(y - d, y + d)范围内的点,这样的点最多只有6个。我们可以利用二分法找到纵坐标大于 y - d的最小的点,然后依次枚举之后的6个点即可。
代码实现在我们实现算法之前,我们需要先生成测试数据,否则如何验证我们的算法是否有问题呢?而且这个算法也是我从头开发的,对于debug也有帮助。
在这道题当中,测试数据还是比较简单的,只需要生成两个随机数作为坐标即可。我们调用这个方法先生成200个点作为测试。
import randomdef random_point():
x, y = random.uniform(0, 1000), random.uniform(0, 1000)
return (x, y)
points = [random_point() for _ in range(200)]
接着我们再实现暴力解法,用来检测我们的算法的正确性,这一段我想应该不用我多说,大家都能理解。
def distance(x, y):return math.sqrt((x[0] - y[0]) ** 2 + (x[1] - y[1])** 2)
def brute_force(points):
ret = sys.maxsize
a, b = None, None
n = len(points)
for i in range(n):
for j in range(i+1, n):
dis = distance(points[i], points[j])
if dis < ret:
ret = dis
a, b = i, j
return ret, points[a], points[b]
最后是重头戏了,其实算法本身的代码量并不大,但是其中的细节不少,稍有不慎就可能翻车。
def divide_algorithm(points):n = len(points)
# 特判只有一个点或者是两个点的情况
if n < 2:
return sys.maxsize, None, None
elif n == 2:
return distance(points[0], points[1]), points[0], points[1]
# 对所有点按照横坐标进行排序
points = sorted(points)
half = (n - 1) // 2
# 递归,这里有一个问题,为什么要先排序再递归?
d1, a1, b1 = divide_algorithm(points[:half])
d2, a2, b2 = divide_algorithm(points[half:])
d, a, b = (d1, a1, b1) if d1 < d2 else (d2, a2, b2)
calibration = points[half][0]
# 根据中间的位置将点集分成两个部分
left, right = [], []
for u in points:
if calibration - d < u[0] < calibration:
left.append(u)
elif calibration <= u[0] < calibration + d:
right.append(u)
# 右侧点集按照纵坐标排序
right = sorted(right, key=lambda x: (x[1], x[0]))
res = d
for u in left:
# 左开右闭的二分
l, r = -1, len(right)-1
while r - l > 1:
m = (l + r) >> 1
if right[m][1] <= u[1] - d:
l = m
else:
r = m
idx = r
# 在范围内最多只有6个点能够构成最近点对
for j in range(7):
if j + idx >= len(right):
break
if distance(u, right[idx + j]) < res:
res = distance(u, right[idx + j])
a, b = u, right[idx + j]
return res, a, b
算法是实现完了,但是仍然有一些细节,比如说为什么我们在分治的时候需要先排序再递归呢?直接分成两个部分递归行不行?为什么不行?比如我们二分的时候使用的是左闭右开的区间二分?
这两个问题我先不给出答案,希望大家能够自己尝试着思考一下。如果有想法的话,欢迎在下方给我留言讨论。
今天的文章就到这里,衷心祝愿大家每天都有所收获。如果还喜欢今天的内容的话,请来一个三连支持吧~(点赞、关注、转发)

