前面我们提到,在防止缓存穿透的情况(缓存穿透是指,缓存和数据库都没有的数据,被大量请求,比如订单号不可能为-1,但是用户请求了大量订单号为-1的数据,由于数据不存在,缓存就也不会存在该数据,所有的请求都会直接穿透到数据库。),我们可以考虑使用布隆过滤器,来过滤掉绝对不存于集合中的元素。
布隆过滤器是什么呢?布隆过滤器(Bloom Filter)是由布隆(Burton Howard Bloom)在1970年提出的,它实际上是由一个很长的二进制向量和一系列随机hash映射函数组成(说白了,就是用二进制数组存储数据的特征)。可以使用它来判断一个元素是否存在于集合中,它的优点在于查询效率高,空间小,缺点是存在一定的误差,以及我们想要剔除元素的时候,可能会相互影响。
也就是当一个元素被加入集合的时候,通过多个hash函数,将元素映射到位数组中的k个点,置为1。
为什么需要布隆过滤器?一般情况下,我们想要判断是否存在某个元素,一开始考虑肯定是使用数组,但是使用数组的情况,查找的时候效率比较慢,要判断一个元素不存在于数组中,需要每次遍历完所有的元素。删除完一个元素后,还得把后面的其他元素往前面移动。
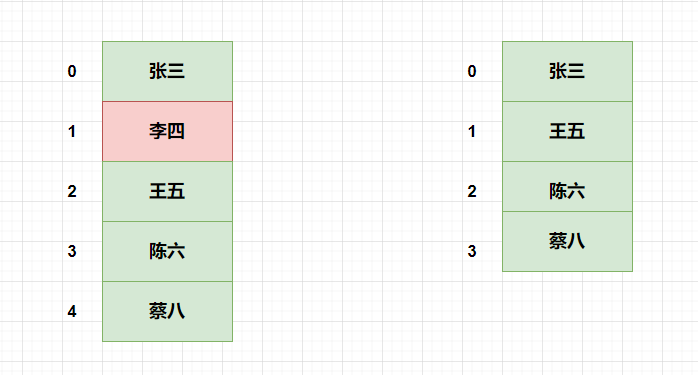
其实可以考虑使用hash表,如果有hash表来存储,将是以下的结构:
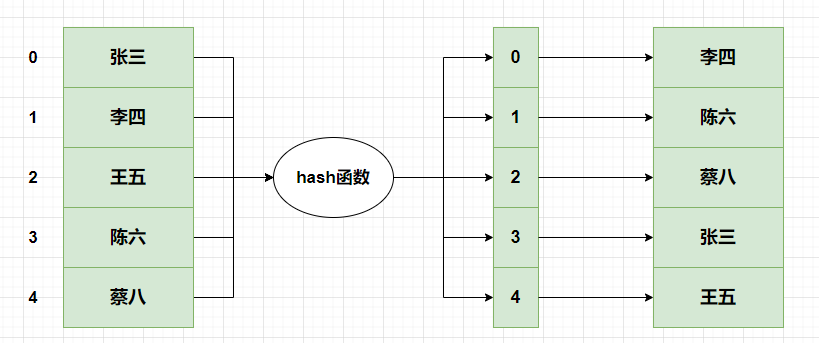
但是这种结构,虽然满足了大部分的需求,可能存在两点缺陷:
只有一个hash函数,其实两个元素hash到一块,也就是产生hash冲突的可能性,还是比较高的。虽然可以用拉链法(后面跟着一个链表)的方式解决,但是操作时间复杂度可能有所升高。
存储的时候,我们需要把元素引用给存储进去,要是上亿的数据,我们要将上亿的数据存储到一个hash表里面,不太建议这样操作。
对于上面存在的缺陷,其实我们可以考虑,用多个hash函数来减少冲突(注意:冲突时不可以避免的,只能减少),用位来存储每一个hash值。这样既可以减少hash冲突,还可以减少存储空间。
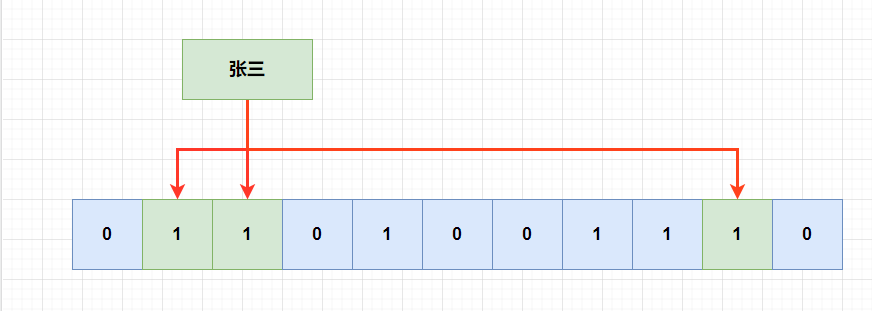
假设有三个hash函数,那么不同的元素,都会使用三个hash函数,hash到三个位置上。

假设后面又来了一个张三,那么在hash的时候,同样会hash到以下位置,所有位都是1,我们就可以说张三已经存在在里面了。
那么有没有可能出现误判的情况呢?这是有可能的,比如现在只有张三,李四,王五,蔡八,hash映射值如下:
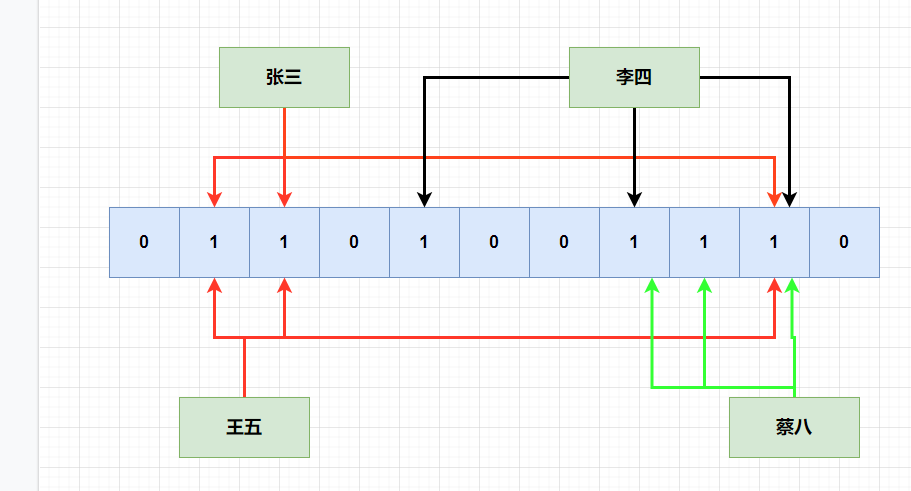
后面来了陈六,但是不凑巧的是,它hash的三个函数hash出来的位,刚刚好就是被别的元素hash之后,改成1了,判断它已经存在了,但是实际上,陈六之前是不存在的。
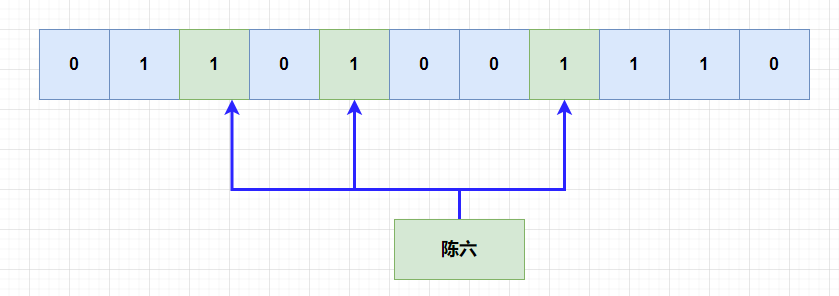
上面的情况,就是误判,布隆过滤器都会不可避免的出现误判。但是它有一个好处是,布隆过滤器,判断存在的元素,可能不存在,但是判断不存在的元素,一定不存在。,因为判断不存在说明至少有一位hash出来是对不上的。
也是由于会出现多个元素可能hash到一起,但有一个数据被踢出了集合,我们想把它映射的位,置为0,相当于删除该数据。这个时候,就会影响到其他的元素,可能会把别的元素映射的位,置为了0。这也就是为什么布隆过滤器不能删除的原因。
具体步骤添加元素:
使用多个hash函数对元素item进行hash运算,得到多个hash值。
每一个hash值对bit位数组取模,得到位数组中的位置索引index。
如果index的位置不为1,那么就将该位置为1。
判断元素是否存在:
使用多个hash函数对元素item进行hash运算,得到多个hash值。
每一个hash值对bit位数组取模,得到位数组中的位置索引index。
如果index所处的位置都为1,说明元素可能已经存在了。
误判率推导庆幸的是,布隆过滤器的误判率是可以预测的,由上面的分析,也可以得知,其实是与位数组的大小,以及hash函数的个数等,这些都是息息相关的。

