搜索是编程的基础,是必须掌握的技能。——王主任 搜索分为盲目搜索和启发搜索
下面列举OI常用的盲目搜索:
1.dijkstra 2.SPFA 3.bfs 4.dfs 5.双向bfs 6.迭代加深搜索(IDFS)下面列举OI常用的启发搜索:
1.最佳优先搜索(A) 2.A* 3.IDA*那么什么是盲目,什么是启发?
举个例子,假如你在学校操场,老师叫你去国旗那集合,你会怎么走? 假设你是瞎子,你看不到周围,那如果你运气差,那你可能需要把整个操场走完才能找到国旗。这便是盲目式搜索,即使知道目标地点,你可能也要走完整个地图。 假设你眼睛没问题,你看得到国旗,那我们只需要向着国旗的方向走就行了,我们不会傻到往国旗相反反向走,那没有意义。 这种有目的的走法,便被称为启发式的。左图为bfs,右图为A
提供一个搜索可视化的链接https://qiao.github.io/PathFinding.js/visual/
搜索算法浅谈 DFS基础中的基础,几乎所有题都可以出一档指数级复杂度暴力分给DFS,同时他的实现也是目录中提到的所有搜索算法中最简单的
dfs的核心思想是:不撞南墙不回头 孙学凤:物理人不撞南墙
举个例子:
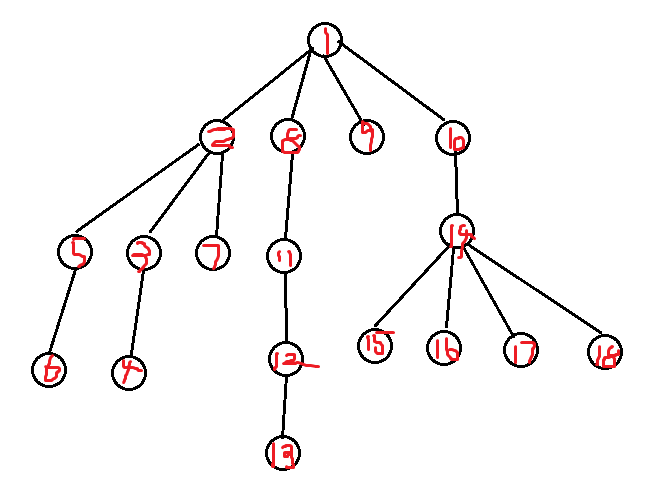
你现在在一号点,你想找到树中与一号点连通的每一个点
那么我们考虑按照深度优先的顺序去遍历这棵树,即,假设你当前在点x,如果和x连边的点中有一个点y,满足y比x深,即y是x的儿子,并且y还没有被访问过,那么我们就走到y,如果有多个y满足条件,我们走到其中任意一个
如果没有y满足条件,我们返回x的父亲
按照这个顺序,我们就可以访问到每个节点,并且每条边会恰好被走两次(从父亲到儿子一次,从儿子到父亲一次)
由于dfs的特性,它有时候会非常的浪费时间,为什么呢?
还是刚才这张图:

如果我们把终点设在10号点,在dfs的过程中要先搜完一号点及其三个子树才能到达终点
代码大体框架:
void dfs(int k){ if(到达目的地或满足条件)输出解 for(int i=1;i<=算符种数;++i){ 保存结果//有时候不需要 dfs(k+1); 回溯结果//有时候不需要 } }那么什么时候需要回溯呢?
我们先要了解回溯的目的:
所以在解题的过程中要判断好是否需要回溯
bfsbfs利用了一种线性数据结构,队列
bfs的核心思想是:从厨师节点开始,生成第一层节点,检查目标节点是否在目标节点中,若没有再将第一层所有的节点逐一扩展,如此往复知道发现目标节点为止
我们再拿出徐瑞帆dalao的图:

你现在还是在一号点,你还是想找到树中与一号点连通的每一个点
我们初始的时候把一号点推入队取出队尾,然后只要当前队列非空,我们就取出队头元素x,并将队头弹出
然后我们将x的所有儿子推入队列
对于图上的情况,我们将所有与x相连,并且还没入过队的点推入队列
这样我们就能够访问所有点
代码大致框架:
void bfs(){ q.push(head); while(!q.empty()){ temp=q.front; q.pop(); if(temp为目标状态)输出解 if(temp不合法)continue; if(temp合法)q.push(temp+Δ); } } IDFS我们已经学会了dfs和bfs
然而有的问题还是使我们无法进行搜索,因为你要进行搜索的图可能是无限大的,每个点所连的边也可能是无限多的,这就使得dfs和bfs都失效了,这时候我们就需要用到idfs
我们枚举深搜的时候深度的上限,因为深度上限的限制,图中的一些边会被删掉,而图就变成了一个有限的图,我们就可以进行dfs了
举个栗子:
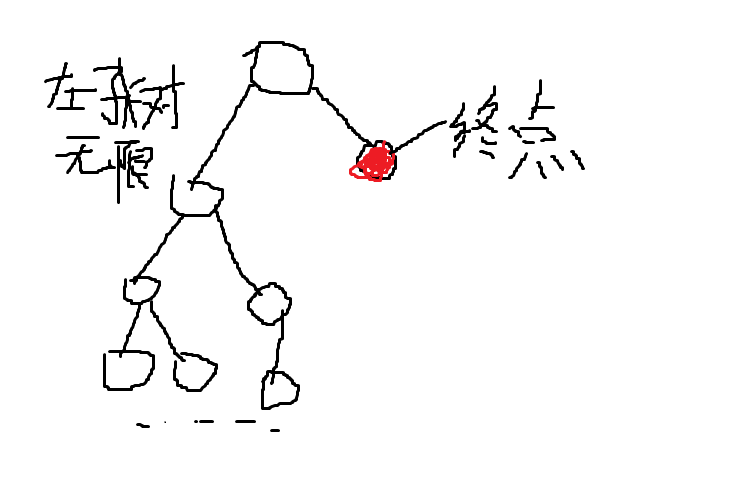
如果用普通的dfs,这显然是一个无解的情况,你将会陷入无限的左子树中
这时,我们设一个深度d,每次搜到第d层就返回搜其他的分支。如果在d层没搜到答案则d++,从头再搜
然而这个算法有一个很明显的缺陷,有一些非答案点要重复搜好几遍,这造成了极大的浪费
于是我们有了IDA*
A在看IDA 之前,我们先了解A*
搜索算法经常运行效率很低,为了提高效率,我们可以使用A*算法
我们对每个点定义一个估价函数f(x)=g(x)+h(x)
g(x)表示从起始点到x的实际代价
h(x)表示估计的从x到结束点的代价,并要求h(x)小于等于从x到结束点的实际代价
那么每次我们从可行点集合中找到f(x)最小的x,然后搜索他
这个过程可以用优先队列(即堆)实现
这样的话可以更快地到达结束点,并保证到达结束点时走的是最优路径
为什么要求h(x)小于等于实际代价呢?
因为如果h(x)大于实际代价的话,可能以一条非最优的路径走到结束点,导致答案变大

