文章: Residual Attention: A Simple but Effective Method for Multi-Label Recognition, ICCV2021
下面说一下我对这篇文章的浅陋之见, 如有错误, 请多包涵指正.
文章的核心方法如下图所示为其处理流程:
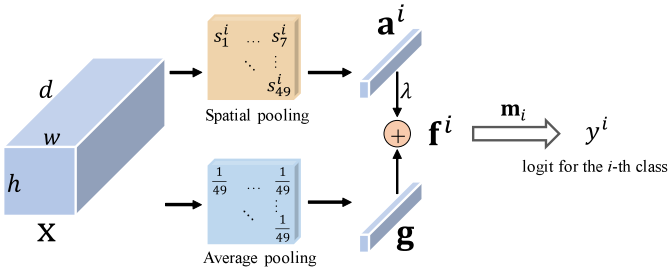
图中 X 为CNN骨干网络提取得到的feature, 其大小为 d*h*w , 为1个batch数据. 一般 d*h*w=2048*7*7 .
从图中可以看到, 有2个分支, 一个是 average pooling, 一个是 spatial pooling, 最后二者加权融合得到 residual attention .
Spatial pooling其过程为:

这里有个 1*1 的卷积操作FC , 其大小为 C*d*1*1 , C 为类别数, 如果直接使用矩阵乘法计算, FC(X) 后的大小为 C*h*w .
但文章中的公式是将其展开为对每个空间点单独计算, 其中 \(\pmb{m_i}\) 为 FC 第i 个类别的参数, 其大小为 d*1*1, 计算得到的 \(s^i_j\) 为第 i 个类别在第 j 个位置的概率, \(\pmb{a^i}\) 为第 i 个类别的特征, 其大小为 d*1 .
如果, \(\pmb{m_i}\) 和 \(\pmb{a^i}\) 计算就可以得到第 i 个类别的概率. 这样就可以用到每个空间点的特征, 有利于不同目标不同类别物体的分类识别.
公式中有个温度参数 T 用来控制 \(s^i_j\) 的大小, 当 T 趋于无穷时, spatial pooling 就变成了 max pooling
Average pooling其过程为:
上式其实就是一般分类模型的做法, 全局均值池化.
Residual Attention如下所示, 将上述2个过程进行加权融合:
其中, \(\pmb{f^i}\) 大小为 d*1, \(\pmb{m_i}^T \pmb{f^i}\) 为第 i 个类别的概率.
至于为什么叫 Residual Attention , 文章中的说法是:
the max pooling among different spatial regions for every class, is in fact a class-specific attention operation, which can be further viewed as a residual component of the class-agnostic global average pooling.
我的理解是, 公式5形式有点像 residual 形式.
文章实验结果 多标签如下表所示为作者对多个数据集的测试, 除了ImageNet 为单标签外, 其它都为多标签. 可以看到多标签提升还是不错的.

由于利用到了不同位置空间点的信息, 获得的 heatmap 会更加准确, 文章中给出了一张结果, 如下:

我觉得这里有个遗憾的是, 文中没有进行对比.
个人理解 关于原理根据流程图, 结合文中作者给出的核心代码, 其基本原理就是 average pooling + max pooling.

上述代码中: y_avg 大小为 C*1, 为 average pooling ; y_max 大小为 C*1, 为 max pooling .
下面是上述代码的一个例子, y_raw 的大小为 1*3*9 , B=1, C=3, H3H, W=3:
可以看到, y_avg 刚好为 average pooling , y_max 刚好为 max pooling .
关于公式公式中的温度参数 T 用于调整参数大小, 而给出的核心代码中, 只有T趋于无穷的情况(等价于max pooling), 对于多个 Head 的情况, T=2,3,4,5 等, 代码中是如何体现出来的?
关于效果对于 multi-label , 使用了 spatial pooling 和 multi-head 来提高效果, 从实验结果来看, 确实有效果, 但对于单标签情况, max pooling 应该改善不大, 从实验结果上看也确实可以看到, 单标签数据集上, 最高提升了0.02个百分点.
测试代码测试代码如下, 可以参考.
import torch from torch import nn class ResidualAttention(nn.Module): def __init__(self, channel=512, num_class=1000, la=0.2): super().__init__() self.la = la self.fc = nn.Conv2d(in_channels=channel, out_channels=num_class, kernel_size=1, stride=1, bias=False) def forward(self, x): y_raw = self.fc(x).flatten(2) # b, num_class, h*w y_avg = torch.mean(y_raw, dim=2) # b, num_class y_max = torch.max(y_raw, dim=2)[0] # b, num_class score = y_avg + self.la * y_max return score if __name__ == '__main__': channel = 4 num_class = 3 batchsize = 1 input = torch.randn(batchsize, channel, 3, 3) resatt = ResidualAttention(channel=channel, num_class=num_class, la=0.2) output = resatt(input) print(output.shape)
