

选择排序也是利用了“挡板法”这个经典思想。
挡板左边是已排序区间,右边是未排序区间,那么每次的“选择”是去找右边未排序区间的最小值,找到之后和挡板后面的第一个值换一下,然后再把挡板往右移动一位,保证排好序的这些元素在挡板的左边。
比如之前的例子:{5, 2, 0, 1}
我们用一个挡板来分隔数组是否排好序, 用指针 j 来寻找未排序区间的最小值;
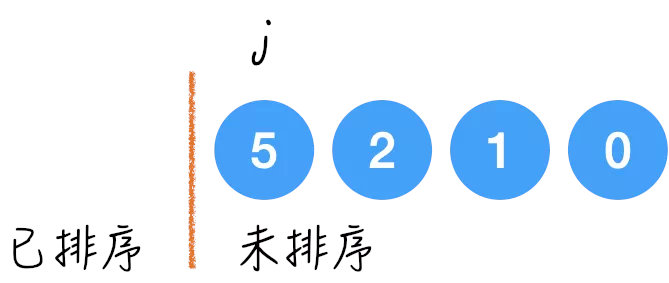
第一轮 j 最初指向 5,然后遍历整个未排序区间,最终指向 0,那么 0 就和挡板后的第一个元素换一下,也就是和 5 交换一下位置,挡板向右移动一位,结束第一轮。

第二轮,j 从挡板后的2开始遍历,最终指向1,然后1和挡板后的第一个元素 2 换一下,挡板向右移动一位,结束第二轮。

第三轮,j 从2开始遍历,最终指向2,然后和2自己换一下,挡板向右移动一位,结束第三轮。

还剩一个元素,不用遍历了,就结束了。
选择排序与之前的插入排序对比来看,要注意两点:
挡板必须从 0 开始,而不能从 1 开始。虽然在这两种算法中,挡板的物理意义都是分隔已排序和未排序区间,但是它们的已排序区间里放的元素的意义不同:
选择排序是只能把当前的最小值放进来,而不能放其他的;
插入排序的第一个元素可以为任意值。
所以选择排序的挡板左边最开始不能有任何元素。
在外层循环时,
选择排序的最后一轮可以省略,因为只剩下最大的那个元素了;
插入排序的最后一轮不可省略,因为它的位置还没定呢。
class Solution {public void selectionSort(int[] input) {
if(input == null || input.length <= 1) {
return;
}
for(int i = 0; i < input.length - 1; i++) {
int minValueIndex = i;
for(int j = i + 1; j < input.length; j++) {
if(input[j] < input[minValueIndex]) {
minValueIndex = j;
}
}
swap(input, minValueIndex, i);
}
}
private void swap(int[] input, int x, int y) {
int tmp = input[x];
input[x] = input[y];
input[y] = tmp;
}
}

最内层的 if 语句每执行一次是 O(1) ,那么要执行多少次呢?
当 i = 0 时,是 n-1 次;
当 i = 1 时,是 n-2 次;
...
最后是 1 次;
所以加起来,总共是: (n-1) + (n-2) + … + 1 = n*(n-1) / 2 = O(n^2)
是这样算出来的,而不是一拍脑袋说两层循环就是 O(n^2).
空间复杂度这个很简单,最多的情况是 call swap() 的时候,然后 call stack 上每一层就用了几个有限的变量,所以是 O(1)。
那自然也是原地排序算法了。
稳定性这个答案是否定的,选择排序并没有稳定性。
因为交换的过程破坏了原有的相对顺序,比如: {5, 5, 2, 1, 0} 这个例子,第一次交换是 0 和 第一个 5 交换,于是第一个 5 跑到了数组的最后一位,且再也无翻身之地,所以第一个 5 第二个 5 的相对顺序就已经打乱了。
这个问题在石头哥的那篇谷歌面经文章里有被考到哦,如果还没有看过这篇面经文章的,在公众号里回复「谷歌」二字,就可以看到了。
优化选择排序的其中一步是选出每一轮的最小值,那么这一步如果使用 heapify() 来优化,就可以从 O(n) 优化到 O(logn),这其实就变成了 heapSort.




