我们先来认识一下树的直径。
树是连通无环图,树上任意两点之间的路径是唯一的。定义树上任意两点\(u, v\)的距离为\(u\)到\(v\)路径上边权的和。树的直径\(MN\)为树上最长路径,即点\(M\)和\(N\)是树上距离最远的两个点,这条路径亦称为树的最长链。
那么,我们考虑一下如何求解树的直径。
方法一:\(DP\)求解树的直径。
设\(d_x\)表示从节点\(x\)出发走向以\(x\)为根的子树,能够达到的最远距离。
那么
\[d_x=\max_{y\in son(x)}\{d_y+e(x,y)\}\]
(\(y\)为\(x\)的一个子节点,\(e(x,y)\)为从\(x\)到\(y\)的权值)
设\(f_x\)代表经过节点\(x\)的最长链的长度,则树的直径为\(\max_{1 \leq x \leq n}\{f_x\}\)。
考虑如何求解\(x\)。对于\(x\)的任意两个子节点\(y_i\)和\(y_j\),\(f_x\)由四部分组成,\(y_i\)到其子树中的最远距离,\(e(y_i,x)\),\(e(x,y_j)\),\(y_j\)到其子树中的最远距离。所以
\[f_x=\max_{y_i,y_j\in son(x)}\{d_{y_i}+d_{y_j}+e(y_i,x)+e(x,y_j)\}\]
注意到\(d_{y_i}+e(y_i,x)\)和\(d_{y_j}+e(y_j,x)\)的格式的相同的,都是用于更新\(d_x\)的项,我们可以在枚举到一个新的\(y\)时利用上一个\(d_x\)的值顺带更\(f_x\),即用\(d_x+d_{y_i}+e(y_i,x)\),实现\(O(n)\)求解树的直径。
\(Code:\)
#include<cstdio> #include<iostream> #include<vector> #include<cstring> #define mset(name,val) memset(name,val,sizeof name) using namespace std; const int N=40000+50; int n,m,ans,vis[N],d[N],f[N]; struct edge{int val,ver;}; vector < edge > Link[N]; inline void input(void) { scanf("%d%d",&n,&m); for(int i=1;i<=m;i++) { int x,y,v; scanf("%d%d%d",&x,&y,&v); Link[x].push_back((edge){v,y}); Link[y].push_back((edge){v,x}); } } inline int dp(int x) { vis[x]=true; for(int i=0;i<Link[x].size();i++) { int y=Link[x][i].ver; if(!vis[y]) { dp(y); f[x]=max(f[x],d[x]+d[y]+Link[x][i].val); d[x]=max(d[x],d[y]+Link[x][i].val); } } ans=max(ans,f[x]); } int main(void) { input(); dp(1); printf("%d\n",ans); return 0; }方法二:两次\(BFS/DFS\)求解树的直径
①从树上任意一点\(P\)出发,找到距离它最远的一点\(M\)
②再从\(M\)出发,找到距离它最远的一点\(N\)
③\(MN\)即为树的直径
时间复杂度\(O(n)\)。
证明如下:
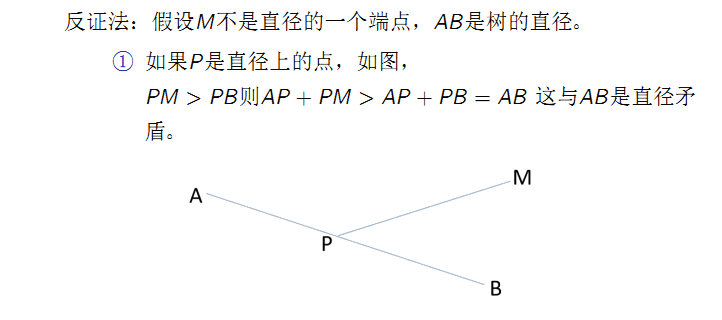
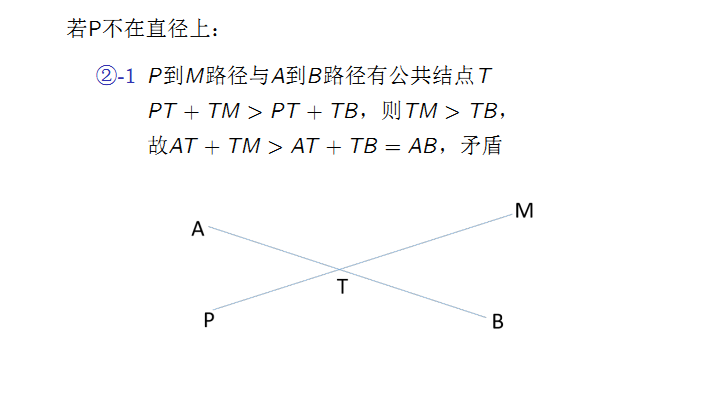
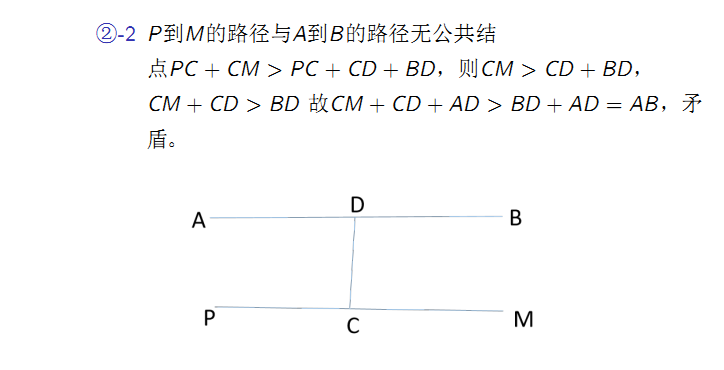
\(Code:\)
#include<cstdio> #include<iostream> #include<queue> #include<vector> #include<cstring> #define mset(name,val) memset(name,val,sizeof name) using namespace std; const int N=40000+50; int n,m,ans,vis[N],dis[N]; struct edge{int val,ver;}; vector < edge > Link[N]; inline void input(void) { scanf("%d%d",&n,&m); for(int i=1;i<=m;i++) { int x,y,v; scanf("%d%d%d",&x,&y,&v); Link[x].push_back((edge){v,y}); Link[y].push_back((edge){v,x}); } } inline int Search(int start) { queue< int >q; mset(vis,0x00); mset(dis,0x00); vis[start]=1; q.push(start); while(!q.empty()) { int temp=q.front();q.pop(); for(int i=0;i<Link[temp].size();i++) { if(!vis[Link[temp][i].ver]) { vis[Link[temp][i].ver]=true; dis[Link[temp][i].ver]=dis[temp]+Link[temp][i].val; q.push(Link[temp][i].ver); } } } int res=0,Maxdis=0; for(int i=1;i<=n;i++) { if(dis[i]>Maxdis) { Maxdis=dis[i]; res=i; } } return res; } int main(void) { input(); int p=Search(1); printf("%d\n",dis[Search(p)]); return 0; }我们通过一道例题详细地了解一下。
Two(POJ1849) DescriptionThe city consists of intersections and streets that connect them.
Heavy snow covered the city so the mayor Milan gave to the winter-service a list of streets that have to be cleaned of snow. These streets are chosen such that the number of streets is as small as possible but still every two intersections to be connected i.e. between every two intersections there will be exactly one path. The winter service consists of two snow plovers and two drivers, Mirko and Slavko, and their starting position is on one of the intersections.
The snow plover burns one liter of fuel per meter (even if it is driving through a street that has already been cleared of snow) and it has to clean all streets from the list in such order so the total fuel spent is minimal. When all the streets are cleared of snow, the snow plovers are parked on the last intersection they visited. Mirko and Slavko don’t have to finish their plowing on the same intersection.
Write a program that calculates the total amount of fuel that the snow plovers will spend.
Input Format
