以上现象公式是可以推导出来的,如下:
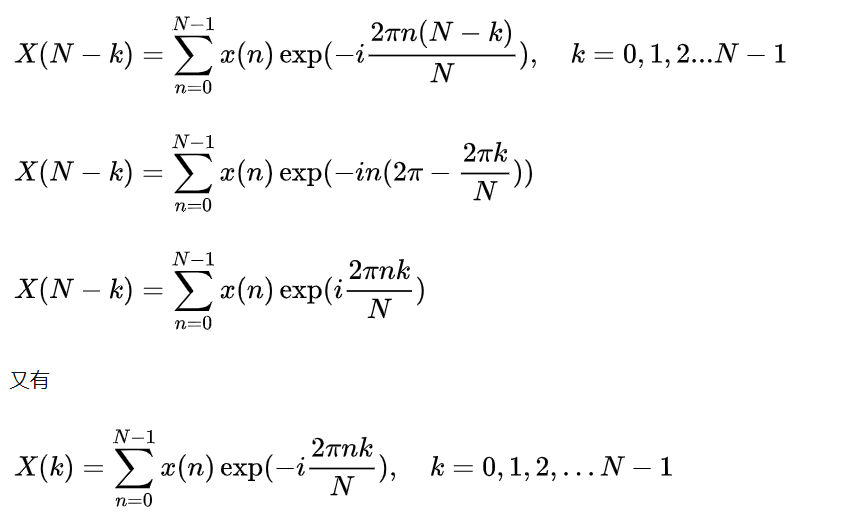
为什么频点40和-40有相同的振幅?因为时域信号是实信号,所谓实信号,即为信号中数据的虚部为0。
所谓共轭,就是实部相同,虚部的符号相反的一对复数。
实信号经过DFT之后,频域信号是共轭对称的,两个数如果共轭,则代表这两个值的幅值相同,相位不同。频点40和-40频点的值是共轭的,所以有相同的振幅。
我们还是以[1, 2, 3]为例子,实信号[1, 2, 3]的频谱是[6 + 0i, -1.5 + 0.86603i, -1.5 - 0.86603i]。
1Hz的-1.5 + 0.86603i和-1Hz的-1.5 - 0.86603i就是共轭对称的。这不是巧合。
这也是暗含在离散傅里叶变换公式中的一个信息。可以推导出来,这还是牵扯到1Hz和-1Hz的频点信息的关系,如下:
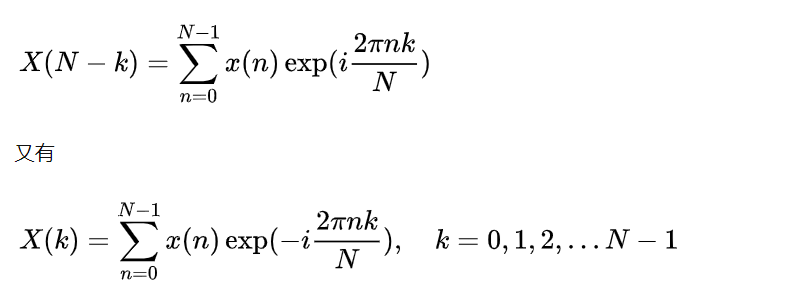
如果x(n)是实信号,那么X(k)与X(N - k)则互为共轭,怎么理解?
其中 $$ e^{-i\times \frac{2\pi nk}{N}} $$ 和 $$ e^{i\times \frac{2\pi nk}{N}} $$ 已经是互为共轭了,就看x(n)的值中的虚部是否为零了。
示意图如下(手残字丑预警):
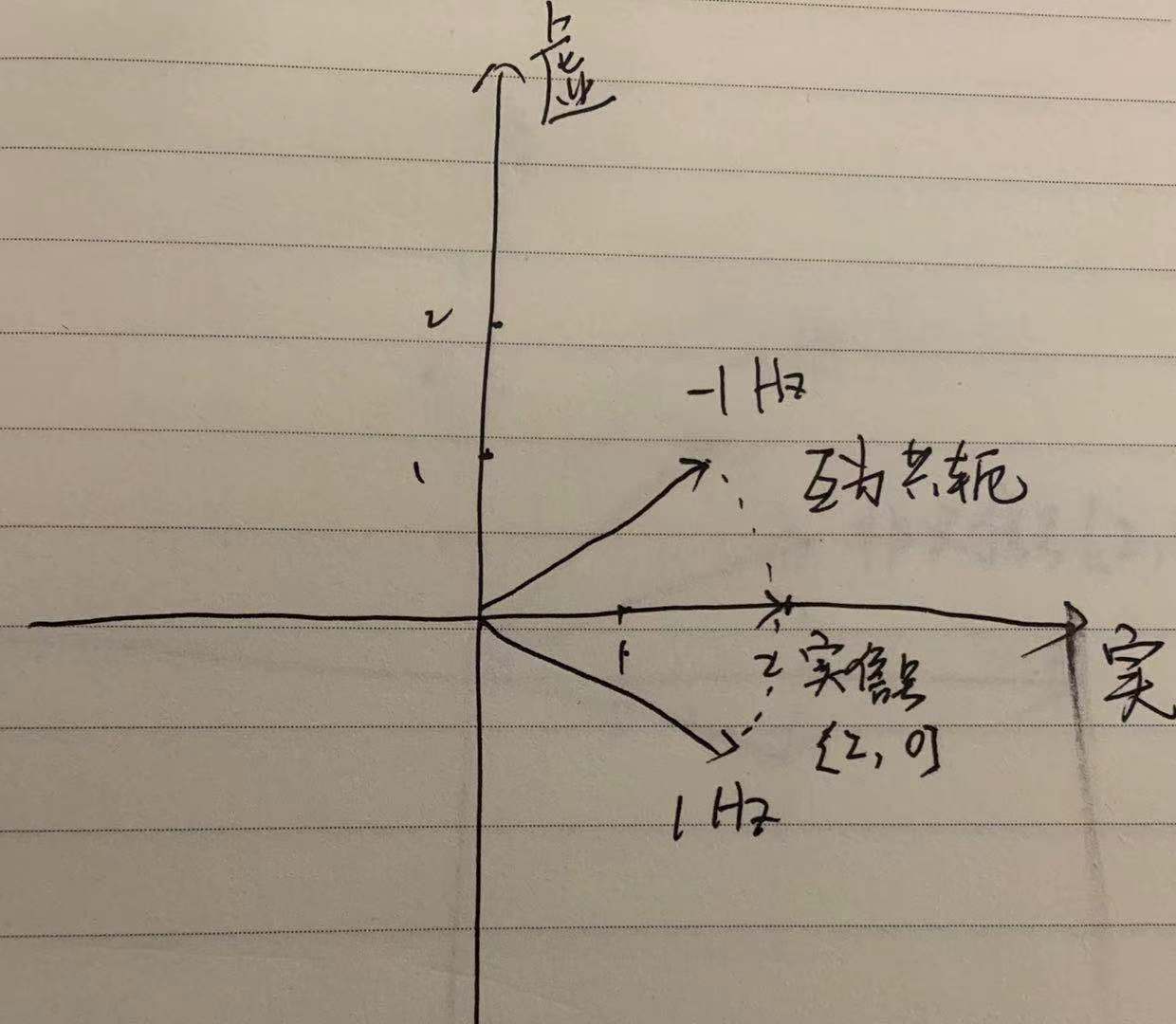
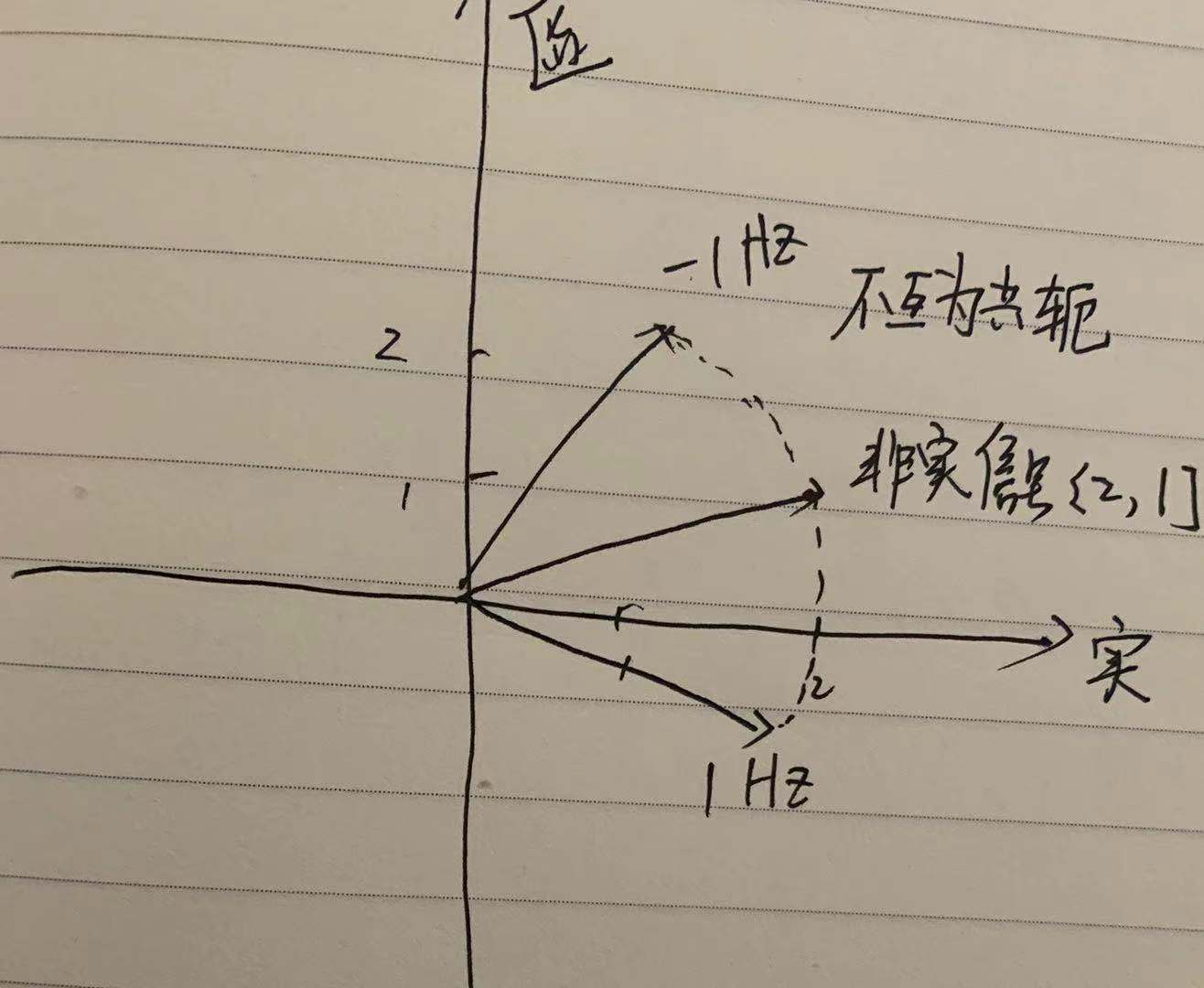
以上简化了生成1Hz的多个向量,仅为示意,但是1Hz和-1Hz频点的关系一目了然,也解释了为什么仅在实信号时,正负频率是共轭的。
思考另一个角度频域信号中所有频点代表的曲线,他们的累加即为时域信号。
想象一下(其实是我不会画图 - -),在一个复平面上如何构建一个,在实部投影是40Hz的cos信号,但虚部投影是0的曲线?
我们是否需要两个复平面曲线,一个如下图,假设它的相位和幅值是a + bi,并且以40Hz的频率逆时针旋转。
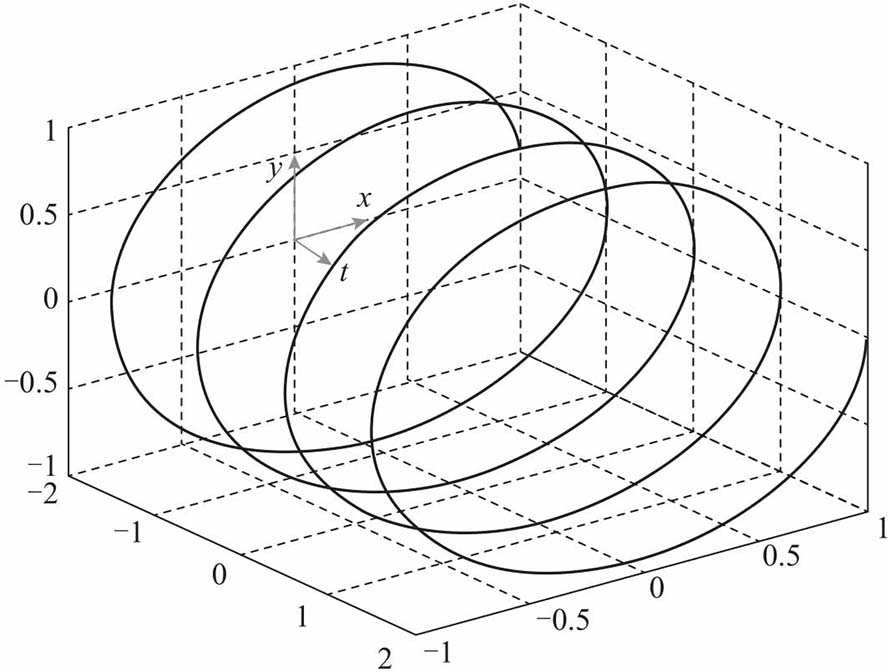
另一个自行脑补,假设它的相位和幅值是a - bi,并且以40Hz的频率顺时针旋转。
以上两个曲线相加,是否能在一个复平面上如何构建一个,在实部投影是40Hz的cos,但虚部投影是0的曲线呢?

