二逼平衡树写得我兹娃乱叫之时,学习了清流的算法——莫队。这次是莫队的进阶版本,资瓷单点修改操作。
原来需要的是两个关键字,而现在多了一维时间。
第一个关键字L表示查询左端点l所在的块的编号,第二个关键字R表示查询右端点r所在块的编号(并不是右端点的值了,因为还有第三维),第三个关键字为时间t。
在这里我们是对修改操作维护的时间轴,之后在查询操作中查找离此次查询操作最近的一次修改操作的时间(请仔细思考)
如果现在的时间比需要的时间大,那么我们让时间倒流,改回原值,剩下的就交给普通莫队了。
我们来对时间复杂度进行证明。
对于一块到底是多少使得时间复杂度最优的问题,我们来分析一下。
以下是luogu题解中的内容对于t轴的移动可以保存每次修改,如果修改在(l,r)间则更新
分块方法可以参照原版莫队,先将l分块,再讲r分块,同一块的按t排序
块大小为
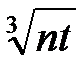
设分块大小为a,莫队算法时间复杂度主要为t轴移动,同r块l,r移动,l块间的r移动三部分
t轴移动的复杂度为


三个函数max的最小值当a为
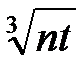
综上所述,一块大小为√n3。
我们直接用STL解决

