五大常见算法策略之——回溯策略 (2)

给定n个重量为w1，w2，w3，...，wn，价值为v1，v2，v3，...，vn的物品和容量为C的背包，求这个物品中一个最有价值的子集，使得在满足背包的容量的前提下，包内的总价值最大。

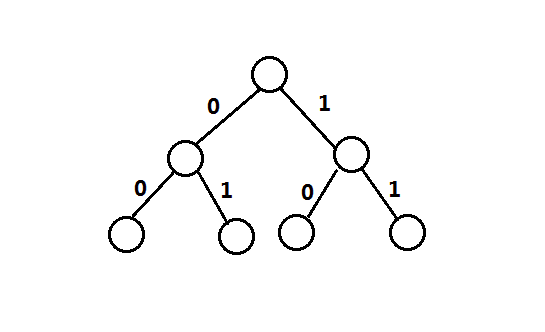
这个问题的解空间树是一棵决策树，每个节点都有两个孩子节点，分别对应了是否将这个物品装入背包的两种情况，0表示不装入，1表示装入，则我们可以画出3件物品的解空间树

package BackTrack; import java.util.Iterator; import java.util.LinkedList; import java.util.List; public class Package { //0-1背包问题，回溯解法 public static final int N = 5; //物品数量 static int[] values = {4,5,2,1,3}; //物品的价值 static int[] weights = {3,5,1,2,2}; //物品的质量 public static final int C = 8; //背包的容量 static int MAX = -1; //记录最大的价值 static int[] bag = {0,0,0,0,0}; //物品放置情况，bag[i] = 0表示第i个物品未被装入，等于1则表示已装入 static List<int[]> list = new LinkedList<int[]>(); //保存最优的结果，可能有多个结果，所以用链表装 public static boolean IsOk(int[] bag, int level) { //判断当前背包是否超重 int weight = 0; for (int i = 0; i <= level; i++) { //计算当前背包中所有的物品的总质量 if(bag[i] == 1) { //bag[i] == 1表示这个物品已被装入背包 weight += weights[i]; if(weight > C) return false; } } return true; } public static void MaxValue(int[] bag, int level) { if(level == N) { //已经判断完最后一个物品 //先计算当前总价值 int value = 0; for (int i = 0; i < N; i++) { if(bag[i] == 1) { value += values[i]; }圆排列 } if(value > MAX) { list.clear(); //发现更优的结果 MAX = value; list.add(bag.clone()); }else if (value == MAX) { //其他放置情况的最优解 list.add(bag.clone()); } return; } for (int i = 0; i < 2; i++) { bag[level] = i; if(IsOk(bag, level)) { MaxValue(bag, level+1); } } } public static void main(String[] args) { MaxValue(bag, 0); System.out.println(MAX); Iterator<int[]> iter = list.iterator(); while(iter.hasNext()) { int[] temp = iter.next(); for (int i = 0; i < temp.length; i++) { System.out.print(temp[i]+" "); } System.out.println(); } } } 图的着色问题

  给定无向连通图G=(V, E)和m种不同的颜色，用这些颜色为图G的各顶点着色，每个顶点着一种颜色。是否有一种着色法使G中相邻的两个顶点有不同的颜色?
  这个问题是图的m可着色判定问题。若一个图最少需要m种颜色才能使图中每条边连接的两个顶点着不同颜色，则称这个数m为该图的色数。求一个图的色数m的问题称为图的m可着色优化问题。
  编程计算：给定图G=(V, E)和m种不同的颜色，找出所有不同的着色法。

形如下面这种情况：

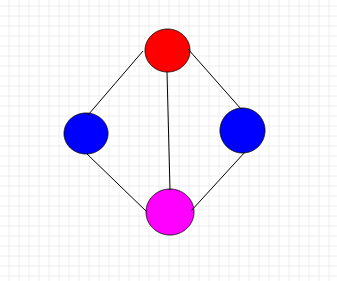
采用回溯策略，对每一个顶点用每一个颜色作尝试，按上图这个例子，3种颜色为这个4个顶点的图着色的解空间树（包括所有可能解和不可能解）有3^4个可能解。即m^n个可能解（m为颜色种数，n为节点个数）。

package BackTrack; import java.util.Scanner; public class Paint { static int[][] p_Maxtrix = new int[4][4]; //图的邻接矩阵 static int Colornum = 3; //颜色数目 static int[] result = {-1,-1,-1,-1}; //保存结果 /** * @param index 当前顶点的下标 * @param color 颜色的编号 * @return 染色方案是否可行 */ public static boolean IsOk(int index, int color) { //判断是否可以染色 for (int i = 0; i < p_Maxtrix.length; i++) { if(p_Maxtrix[index][i] == 1 && result[i] == color) { return false; } } return true; } public static void backtrack(int index) { if(index == p_Maxtrix.length) { //完成最后一个顶点的着色，输出其中一种结果 for (int i = 0; i < result.length; i++) { System.out.print(result[i]+" "); } System.out.println(); return; } for (int i = 0; i < Colornum; i++) { //对每一种颜色进行尝试 result[index] = i; if(IsOk(index, i)) { backtrack(index+1); } result[index] = -1; } } public static void main(String[] args) { Scanner in = new Scanner(System.in); for (int i = 0; i <p_Maxtrix.length ; i++) { for (int j = 0; j < p_Maxtrix.length; j++) { p_Maxtrix[i][j] = in.nextInt(); } } backtrack(0); } } 圆排列问题