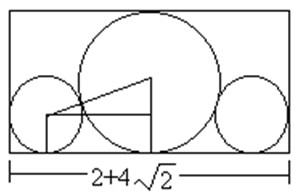
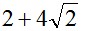给定n个大小不等的圆c1,c2,…,cn,现要将这n个圆排进一个矩形框中,且要求各圆与矩形框的底边相切。圆排列问题要求从n个圆的所有排列中找出有最小长度的圆排列。例如,当n=3,且所给的3个圆的半径分别为1,1,2时,这3个圆的最小长度的圆排列如图所示。其最小长度为
算法思路:将每个圆在每个位置上的所有可能作全排列,找出最短距离。
swap函数:用于交换圆之间的顺序,将两个圆互换位置。
center函数:计算第t个圆的圆心的坐标,用于给x数组赋值。
compute函数:其实是在当将最后一个圆排列完成后的操作,计算出当前的排列的距离,与已知的最优解比较,若更优就更新最优解。
backtrack函数:对每一种排列组合进行回溯尝试。
参考博文:圆排列
package BackTrack; public class Round { public static final int N = 3; //圆的数目 static double min = 1000; //最短距离 static double[] x = new double[N]; //每个圆的圆心 static int[] r = {1,1,2}; //每个圆的半径 static int[] best = new int[N]; //最优解 //交换函数,交换某两个圆的位置 public static void swap(int[] a, int x, int y) { int temp1 = a[x]; int temp2 = a[y]; a[x] = temp2; a[y] = temp1;位置 } /** * 对为什么要使用循环做一解释: * 因为可能存在第x个圆,它太过于小,而导致其对第x-1和x+1,甚至其他的圆来说,第x个圆存在于不存在都是没影响的 * 取x-1,和x+1来说:可能x太小,x+1与x-1相切,所以计算第x+1圆心坐标的时候,只能以x-1的圆心与它的圆心来计算 * 所以要每次循环比较选择最大的那一个做半径 * 可以参考https://blog.csdn.net/qq_37373250/article/details/81477394中的图 */ public static double center(int t) { double max = 0.0; //默认第一个圆的圆心是0.0 for(int i = 0; i < t; i++) { double temp = x[i]+2.0*Math.sqrt(r[i]*r[t]); //计算得到“以第i个圆的半径和待计算圆的半径”得出的圆心 //取最大值 if(temp > max) { max = temp; } } return max; } /** * 针对为什么不能直接temp = x[N-1]+x[0]+r[N-1]+r[0](直接用第一个圆到最后一个圆的圆心距离加上两圆半径)做一解释: * 为避免第一个圆太小,而第二个圆太大,而导致第二个圆的边界甚至超过了第一个圆的边界,最右边同理 * 那也可以依次推出可能第三个,第四个...的边界超过了第一个圆的边界,右边同理,所以需要每一个都做一下比较 * 但是可以放心,x是按圆当前排列顺序放置圆心坐标的 */ public static void compute() { //计算按此排列得到的结果 double low = 0, high = 0; //分别表示最左边的边际,和最右边的边际 for(int i = 0; i < N; i++) { if(x[i]-r[i] < low) { low = x[i]-r[i]; } if(x[i]+r[i] > high) { high = x[i]+r[i]; } } double temp = high - low; if(temp < min) { min = temp; for (int i = 0; i < N; i++) { best[i] = r[i]; } } } public static void backtrack(int t) { if(t == N) { compute(); //return; } for(int i = t; i < N; i++) { //t之前的圆已经排好顺序了,可能不是最优解,但是一种可能解 swap(r, t, i); double center_x = center(t); x[t] = center_x; backtrack(t+1); /*下面是使用了较为简陋的剪枝算法进行优化 if(center_x+r[i] < min) { x[t] = center_x; backtrack(t+1); } */ swap(r, t, i); //恢复交换之前的 } } public static void main(String[] args) { backtrack(0); for (int i = 0; i < N; i++) { System.out.print(best[i]+" "); } System.out.println(); System.out.println(min); } } 连续邮资问题假设国家发行了n种不同面值的邮票,并且规定每张信封上最多只允许贴m张邮票。连续邮资问题要求对于给定的n和m的值,给出邮票面值的最佳设计,在1张信封上可贴出从邮资1开始,增量为1的最大连续邮资区间。例如,当n=5和m=4时,面值为(1,3,11,15,32)的5种邮票可以贴出邮资的最大连续邮资区间是1到70。
解法思路:解决这个问题其实不光用到回溯,还用到了前面的动态规划策略。
首先要明确必须要有一张面值为1的邮票,否则连刚开始一元的邮资都无法贴出。
然后就是第x张邮票的面值必须介于第x-1张邮票的面值+1和前x-1张邮票所能贴出的最大邮资+1之间(闭区间)
明确前面两点后,回溯的方法就很简单了。每层都是在上一层的面值+1和上一层最大邮资+1之间对所有的可能进行尝试求解最优解。