五大常见算法策略之——回溯策略

回溯是五大常用算法策略之一，它的核心思想其实就是将解空间看作是一棵树的结构，从树根到其中一个叶子节点的路径就是一个可能的解，根据约束条件，即可得到满足要求的解。求解问题时，发现到某个节点而不满足求解的条件时，就“回溯”返回，尝试别的路径。回溯法是一种选优搜索法，按选优条件向前搜索，以达到目标。下面通过几个例子来讨论这个算法策略。

货郎问题

有一个推销员，要到n个城市推销商品，他要找出一个包含所有n个城市的具有最短路程的环路。（最后回到原来的城市），也就是说给一个无向带权图G<V,E>,用一个邻接矩阵来存储两城市之间的距离（即权值），要求一个最短的路径。

我们设置一组数据如下：4个城市，之间距离如下图所示，默认从0号城市出发

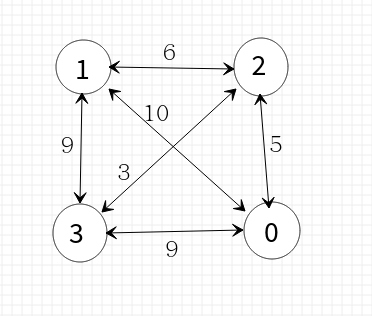
由此我们可以画出一棵解空间树：（只画了一部分，右边同理）

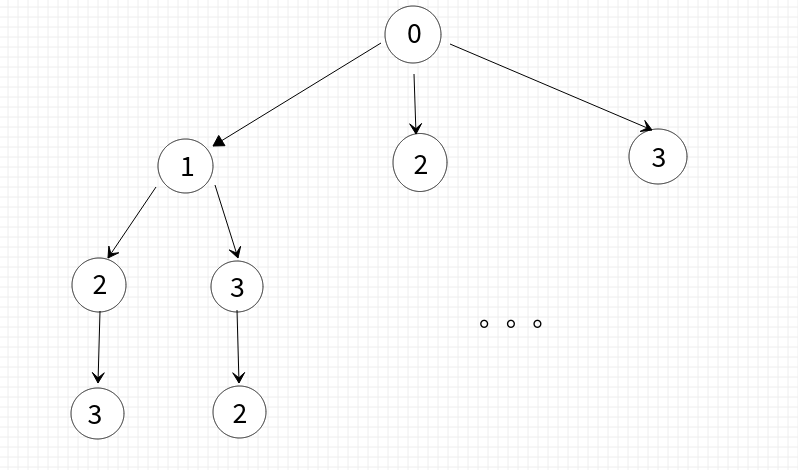
按照这个解空间树，对其进行深度优先搜索，通过比较即可得到最优结果（即最短路径）

package BackTrack; //解法默认从第0个城市出发，减小了问题难度，主要目的在于理解回溯策略思想 public class Saleman { //货郎问题的回溯解法 static int[][] map = { { 0,10,5,9}, {10,0,6,9}, { 5,6,0,3}, { 9,9,3,0} }; //邻接矩阵 public static final int N = 4; //城市数量 static int Min = 10000; //记录最短的长度 static int[] city = {1,0,0,0}; //默认第0个城市已经走过 static int[] road = new int[N]; //路线，road[i] = j表示第i个城市是第j个经过的 /** * * @param city 保存城市是否被经过，0表示未被走过，1表示已经走过 * @param j 上一层走的是第几个城市 * @param len 此时在当前城市走过的距离总和 * @param level 当前所在的层数，即第几个城市 */ public static void travel(int[] city, int j, int len, int level) { if(level == N - 1) { //到达最后一个城市 /*do something*/ if(len+map[j][0] < Min) { Min = len + map[j][0]; for (int i = 0; i < city.length; i++) { road[i] = city[i]; } } return; } for(int i = 0; i < N; i++) { if(city[i] == 0 && map[j][i] != 0) { //第i个城市未被访问过，且上一层访问的城市并不是此城市 city[i] = level+2; //将此城市置为已访问 travel(city, i, len+map[j][i], level+1); city[i] = 0; //尝试完上一层的路径后，将城市又置为未访问，以免影响后面的尝试情况，避免了clone数组的情况，节省内存开销 } } } public static void main(String[] args) { travel(city,0,0,0); System.out.println(Min); for (int i = 0; i < N; i++) { System.out.print(road[i]+" "); } System.out.println("1"); } } 八皇后问题

要在n*n的国际象棋棋盘中放n个皇后，使任意两个皇后都不能互相吃掉。规则：皇后能吃掉同一行、同一列、同一对角线的任意棋子。求所有的解。n=8是就是著名的八皇后问题了。

  用一个position数组表示皇后的摆放位置，position[i] = j表示第i行皇后放在第j列，我们从第一行开始，对每一列进行尝试摆放，如果可行则继续第二行，同理第二行继续对每一列进行尝试，如果发现某一行不管放在哪一列都不可行，说明上面某行的摆放是不可行的，则回溯到上面一行，从摆放的那一列接着往下尝试......

  这道题的解空间树非常庞大，第一层8个节点，然后往下每一个节点又有8个孩子（包含了所有可行和不可行解，但都要尝试过去），所以有8^8种可能解。

public class Empress { final static int N = 8; //皇后个数 static int count = 0; //输出的结果个数 static int[] postion = new int[N]; //保存每一行皇后摆放的位置，position[i] = j表示第i行皇后放在第j列 /** * @param row 判断第row行摆放是否合理 * @return 合理返回true，否则false */ public static boolean IsOk(int row){ for (int i = 0; i < row; i++) { //和前面的每一行进行对比 if(postion[i] == postion[row] || Math.abs(i-row) == Math.abs(postion[i] - postion[row])){ //如果在同一列则postion[i] == postion[row] //如果在同一斜线上Math.abs(i-row) == Math.abs(postion[i] - postion[row]) return false; } } return true; } public static void Print(){ System.out.println("This is the No."+(++count)+" result:"); for (int i = 0; i < N; i++) { //i为行序号 for (int j = 0; j < N; j++) { //j为第i行皇后的列的序号 if(postion[i] == j){ //不是皇后的拜访地址 System.out.print("# "); }else{ System.out.print("@ "); } } System.out.println(); //换行 } } /** * @param row 尝试第row行皇后的摆放位置，找到可行位置就继续深度搜索下一行，否则在尝试完i的所有取值无果后回溯 */ public static void backtrack(int row){ if(row == N){ //若已经等于N，则说明0~N-1已经赋值完毕，直接打印返回 Print(); return; } for (int i = 0; i < N; i++) { postion[row] = i; //第row行皇后的位置在i处 if(IsOk(row)){ backtrack(row+1); }else{ /** * 如果第row行的皇后拜访在i(0-N)处可行，则继续向下深度搜索，否则就直接让这层递归函数出栈 * 此层函数出栈也就是当前结点不满足继续搜索的限制条件，即回溯到上一层，继续搜索上一层的下一个i值 */ } } } public static void main(String[] args) { backtrack(0); } } 0-1背包的回溯解法