big-O notation and its relatives-concepts that belong in the vocabulary of every serious programmer and computer scientist.
为什么要研究它
渐进表示法是算法分析里的基本术语,当听到别人说某段代码以"n的大O时间"运行,而另一段代码以"n平方的大O时间 运行",你需要知道背后的含义。
当某个问题可以用不同的算法解决时,需要用一个东西进行比较哪个算法好。渐进表示算法就可以帮助区分。
High Level
一句话概括渐进算法,就是: 忽略常数因子和低阶项。

渐进法还有更多的含义,但是10年后能记得的就是上面这个概括,它很精妙。
为什么要忽略常数因子?
常数因子一般很依赖于环境的细节,我们的算法分析是不想固定某种特定的编程语言,计算机体系结构,所以忽略常数因子是合理的。
为什么要忽略低阶项?
当我们的输入很大的时候,低阶项的作用很微小,而我们算法关注的就是大规模的输入。
大O符号
标准的数学公式如下定义:

T(n)=O(f(n))当且仅当T(n)最后的上界是f(n)的一个常数积。
所以只需要找的到c和n0,使得当n>=n0的时候不等式满足,就表示T(n)=O(f(n))。
用图来表示就是
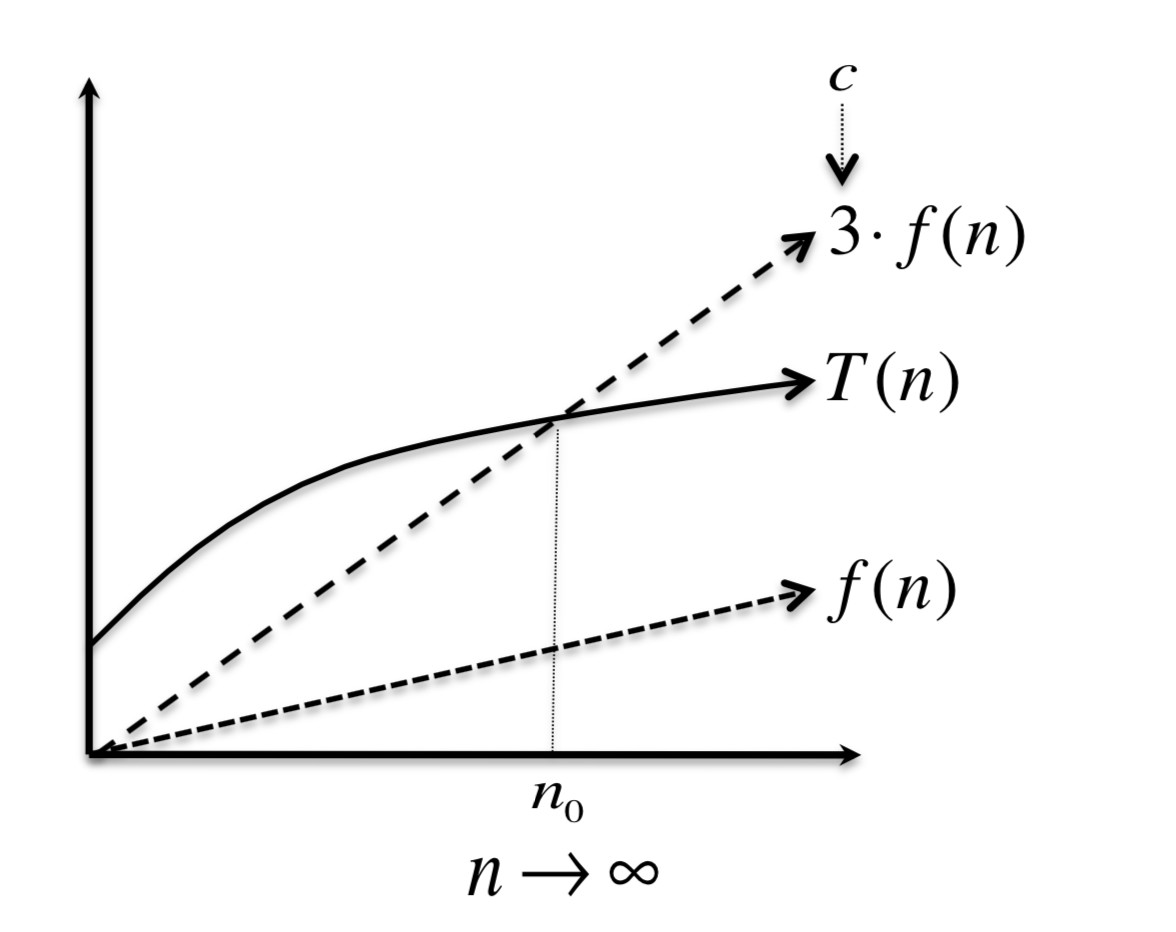
这里的n0就是指'最后的',3就是指'常数倍',当n>n0的时候,满足T(n)<=3f(n),所以T(n)=O(f(n))。
大Omega符号
它的数学表示如下:

它的定义和大O的定义是平行的,当且仅当T(n)最后的下界是f(n)的一个常数积。用图来表示就是:
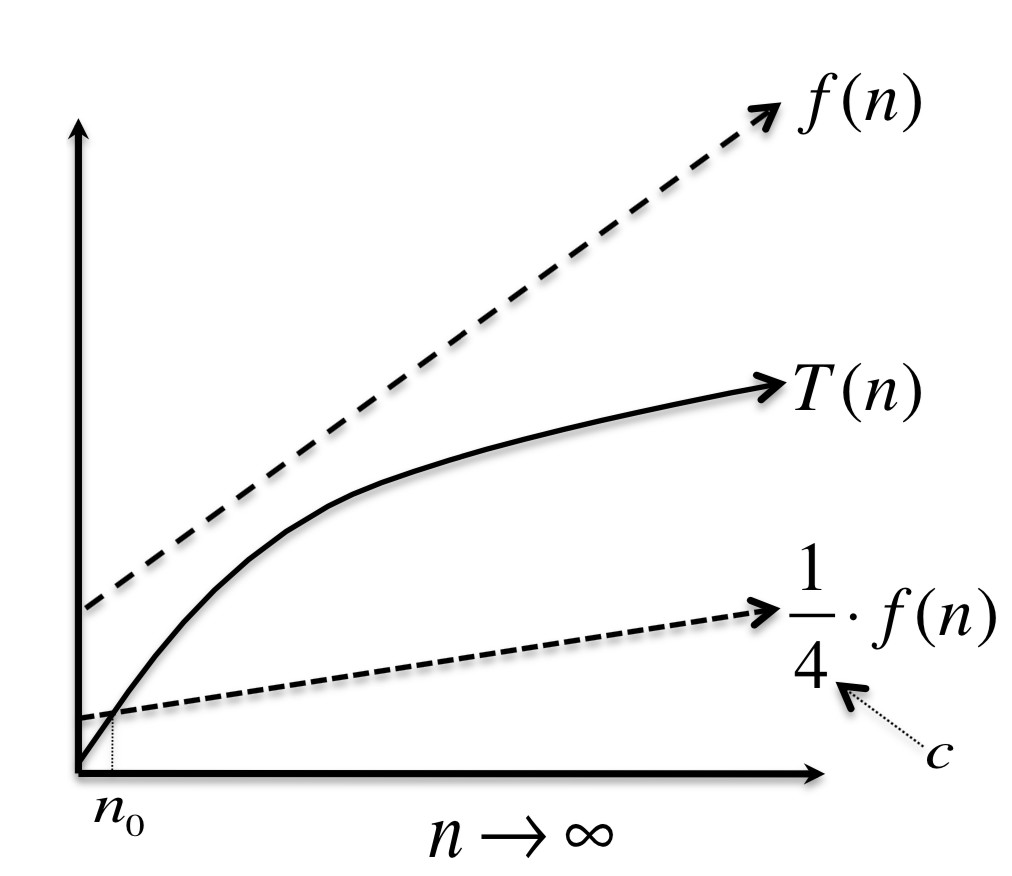
当n>=n0时,T(n)>=1/4f(n),所以
大theta符号
可以把它类比为"等于",同时满足上面两个条件,即:
和
相当于T(n)最后被夹在了f(n)的两个不同的常数积之间。数学定义如下:

参考书:Algorithms Illuminated

