忽略第一步找到的最大元素,重复执行第一步,直到全部元素有序
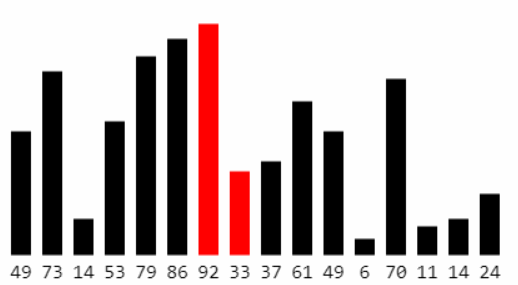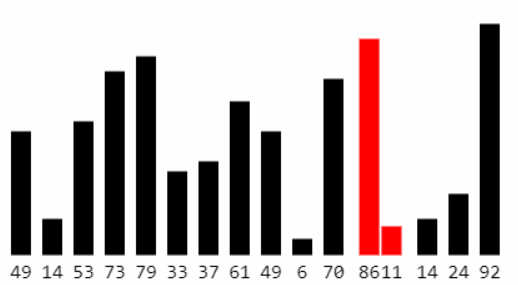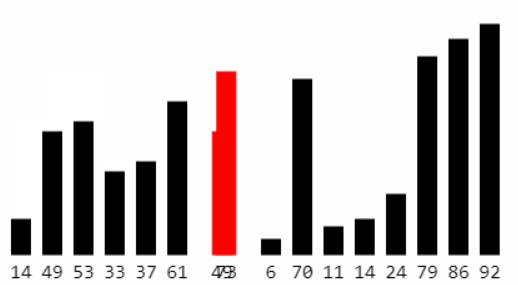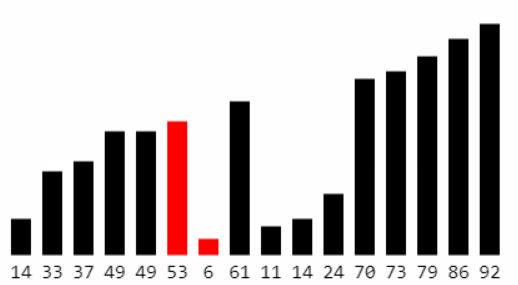
3.2 基本实现
public void sort() {
for (int eIndex = array.length - 1; eIndex > 0; eIndex--) {
for (int i = 1; i <= eIndex; i++) {
if (cmp(i, i - 1) < 0) {
swap(i, i - 1);
}
}
}
}
3.4 优化一
优化方案:如果序列已经完全有序,可以提前终止冒泡排序
缺点:只有当完全有序时才会提前终止冒泡排序,概率很低
public void sort() {
for (int eIndex = array.length - 1; eIndex > 0; eIndex--) {
boolean sorted = true;
for (int i = 1; i <= eIndex; i++) {
if (cmp(i,i - 1) < 0) {
swap(i, i - 1);
sorted = false;
}
}
if (sorted) break;
}
}
3.5 优化二
优化方案:如果序列尾部已经局部有序,可以记录最后一次交换的位置,减少比较次数

public class BubbleSort<T extends Comparable<T>> extends Sort<T> {
/**
* 优化方式二:如果序列尾部已经局部有序,可以记录最后依次交换的位置,减少比较次数
* 为什么这里sortedIndex为1(只要保证 eIndex-- > 0 即可)?
*
=> 如果sortedIndex为eIndex,当数组第一次就完全有序时,就退回到最初的版本了
*
=> 如果sortedIndex为1,当数组第一次就完全有序时,一轮扫描就结束了!
*
*/
@Override
public void sort() {
for (int eIndex = array.length - 1; eIndex > 0; eIndex--) {
int sortedIndex = 1; //记录最后一次交换的下标位置
for (int i = 1; i <= eIndex; i++) {
if (cmp(i, i - 1) < 0) {
swap(i, i - 1);
sortedIndex = i;
}
}
eIndex = sortedIndex;
}
}
}
3.6 算法优劣
最坏,平均时间复杂度:O(n^2),最好时间复杂度:O(n)
空间复杂度:O(1)
属于稳定排序



