注意:稍有不慎,稳定的排序算法也能被写成不稳定的排序算法,如下冒泡排序是不稳定的
public void sort() {
for (int eIndex = array.length - 1; eIndex > 0; eIndex--) {
for (int i = 1; i <= eIndex; i++) {
if (cmp(i, i - 1) <= 0) {
swap(i, i - 1);
}
}
}
}
属于原地算法
4. 选择排序(Selection Sort)
4.1 执行流程
从序列中找出最大的哪个元素,然后与最末尾的元素交换位置。执行完一轮后最末尾那个元素就是最大的元素
忽略第一步找到的最大元素,重复执行第一步
这里以选最小元素为例
4.2 基本实现
public class SelectionSort<T extends Comparable<T>> extends Sort<T> {
@Override
public void sort() {
for (int eIndex = array.length - 1; eIndex > 0; eIndex--) {
int maxIndex = 0;
for (int i = 1; i <= eIndex; i++) {
//注意:为了稳定性,这里要写 <=
if (cmp(maxIndex, i) <= 0) {
maxIndex = i;
}
}
if(maxIndex != eIndex) swap(maxIndex, eIndex);
}
}
}
4.3 算法优劣
选择排序的交换次数要远少于冒泡排序,平均性能优于冒泡排序
最好,最坏,平均时间复杂度均为O(n^2),空间复杂度为O(1),属于不稳定排序
选择排序是否还有优化的空间? => 使用堆来选择最大值
5. 堆排序(Heap Sort)
堆排序可以认为是对选择排序的一种优化
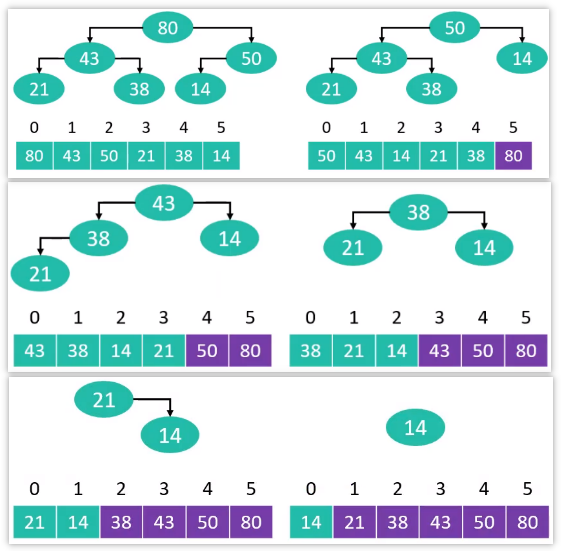
5.1 执行流程
对序列进行原地建堆(heapify)
重复执行以下操作,直到堆的元素数量为1
交换堆顶元素与尾元素
堆的元素数量减1
对0位置进行一次siftDown操作
5.2 基本实现
public class HeapSort<T extends Comparable<T>> extends Sort<T> {
/** 记录堆数据 */
private int heapSize;
@Override
protected void sort() {
// 原地建堆(直接使用数组建堆)
heapSize = array.length;
for (int i = (heapSize >> 1) - 1; i >= 0; i--) {
siftDown(i);
}
while (heapSize > 1) {
// 交换堆顶元素和尾部元素
swap(0, --heapSize);
// 对0位置进行siftDown(恢复堆的性质)
siftDown(0);
}
}
/** 堆化 */
private void siftDown(int index) {
T element = array[index];
int half = heapSize >> 1;
while (index < half) { // index必须是非叶子节点
// 默认是左边跟父节点比
int childIndex = (index << 1) + 1;
T child = array[childIndex];
int rightIndex = childIndex + 1;
// 右子节点比左子节点大
if (rightIndex < heapSize &&
cmp(array[rightIndex], child) > 0) {
child = array[childIndex = rightIndex];
}
// 大于等于子节点
if (cmp(element, child) >= 0) break;
array[index] = child;
index = childIndex;
}
array[index] = element;
}
}
5.2 算法优劣
最好,最坏,平均时间复杂度:O(nlog^n)
空间复杂度:O(1)
属于不稳定排序
5.3. 冒泡,选择,堆排序比较
@SuppressWarnings({"rawtypes","unchecked"})
public class SortTest {
public static void main(String[] args) {
Integer[] arr1 = Integers.random(10000, 1, 20000);
testSort(arr1,
new SelectionSort(),
new HeapSort(),
new BubbleSort());
}
static void testSort(Integer[] arr,Sort... sorts) {
for (Sort sort: sorts) {
Integer[] newArr = Integers.copy(arr);
sort.sort(newArr);
//检查排序正确性
Asserts.test(Integers.isAscOrder(newArr));
}
Arrays.sort(sorts);
for (Sort sort: sorts) {
System.out.println(sort);
}
}
}

6. 插入排序(Insertion Sort)
6.1 执行流程
在执行过程中,插入排序会将序列分为两部分(头部是已经排好序的,尾部是待排序的)
从头开始扫描每一个元素,每当扫描到一个元素,就将它插入到头部适合的位置,使得头部数据依然保持有序
6.2 基本实现
public class InsertionSort<T extends Comparable<T>> extends Sort<T> {
@Override
protected void sort() {
for (int i = 1; i < array.length; i++) {
int cur = i;
while(cur > 0 && cmp(cur,cur - 1) < 0) {
swap(cur,cur - 1);
cur--;
}
}
}
}
6.3 逆序对(Inversion)
什么是逆序对? => 数组 [2,3,8,6,1] 的逆序对为:<2,1> < 3,1> <8,1> <8,6> <6,1>
插入排序的时间复杂度与逆序对的数量成正比关系





