

7.2 思路
merge
大致想法

细节
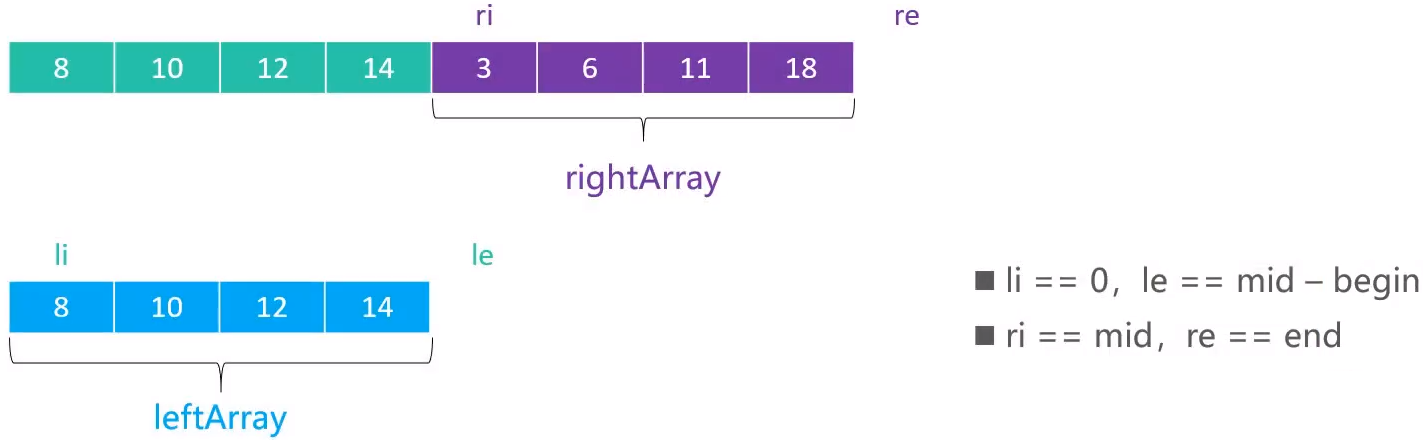
需要 merge 的 2 组序列存在于同一个数组中,并且是挨在一起的

为了更好的完成 merge 操作,最好将其中 1 组序列备份出来,比如 [begin,mid)
基本实现

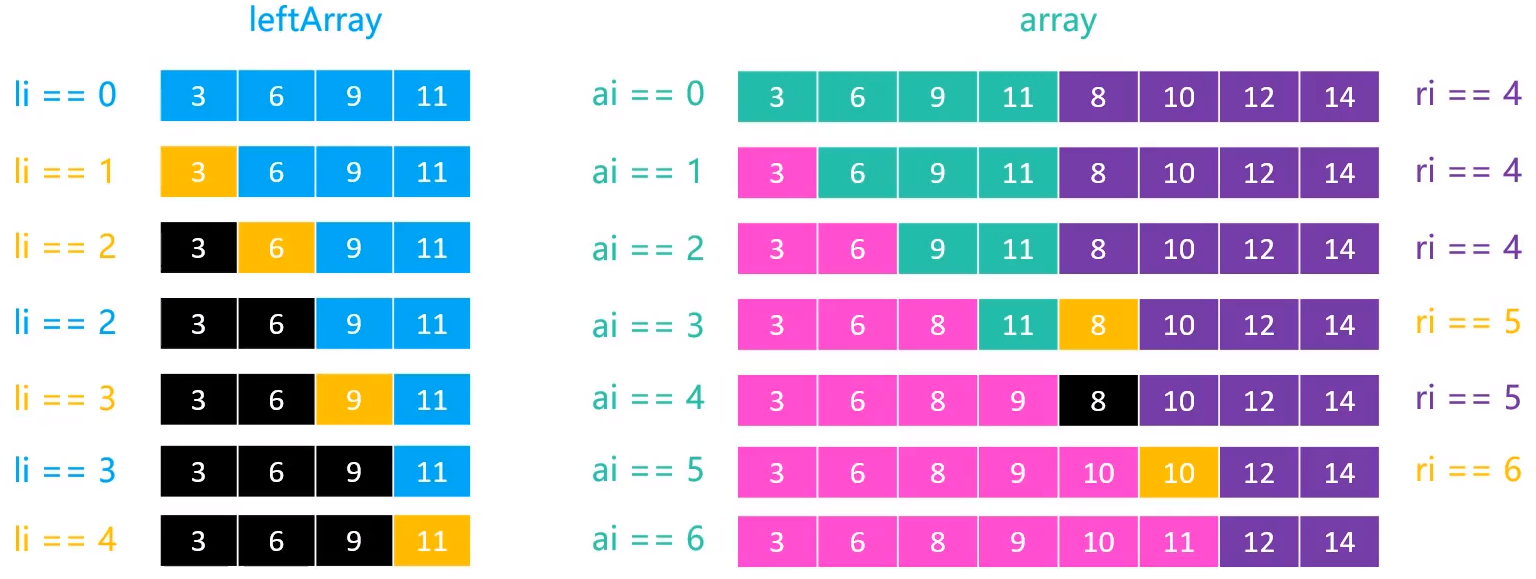
情况一:左边先结束 => 左边一结束整个归并就结束
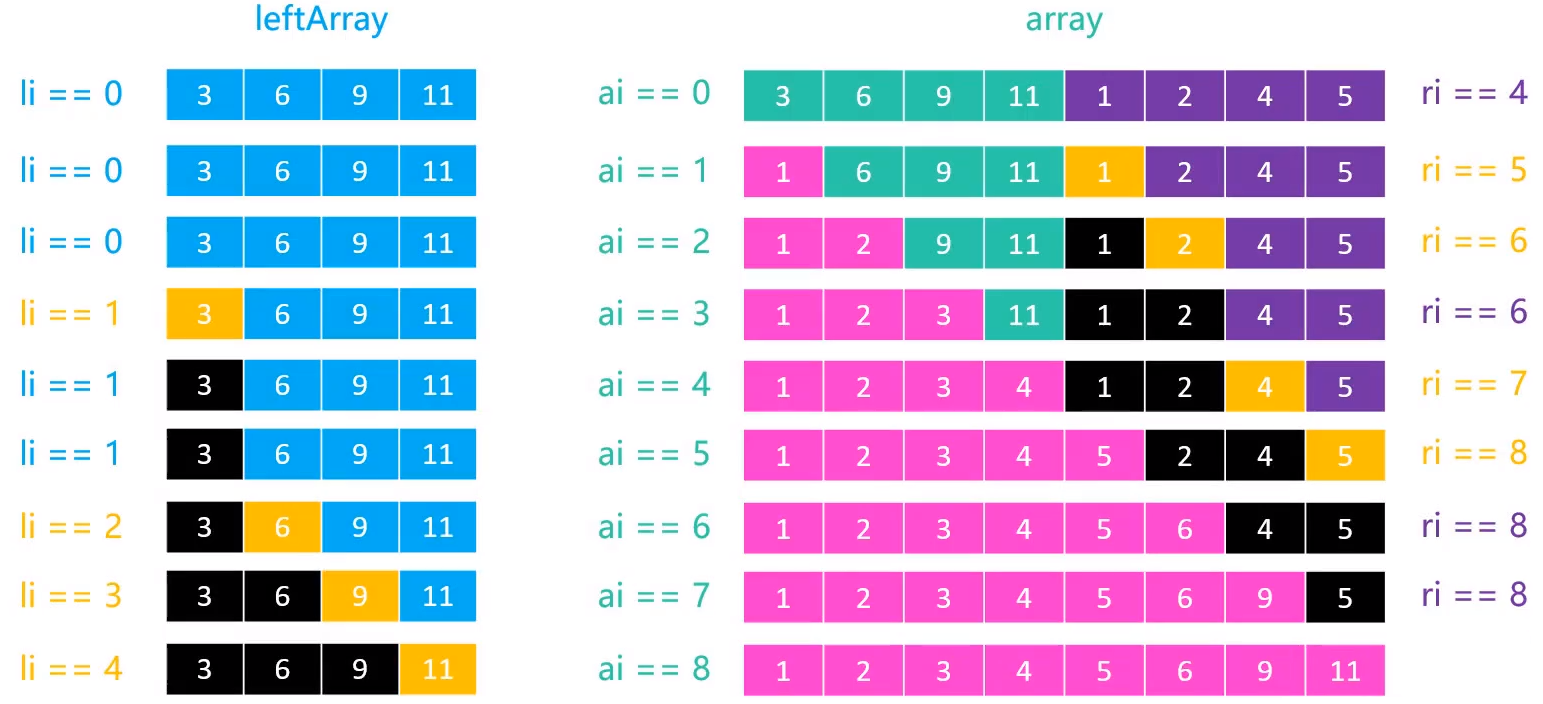
情况二:右边先结束 => 右边一结束就直接将左边按顺序挪到右边去
7.3 基本实现
@SuppressWarnings("unchecked")
public class MergeSort<T extends Comparable<T>> extends Sort<T> {
private T[] leftArr;
@Override
protected void sort() {
leftArr = (T[]) new Comparable[array.length >> 1];
sort(0, array.length);
}
/** 对 [begin,end) 位置的元素进行归并排序 */
private void sort(int begin, int end) {
if (end - begin < 2) return;
int mid = (begin + end) >> 1;
sort(begin, mid);
sort(mid, end);
merge(begin, mid, end);
}
/** 将 [begin,mid) 和 [mid,end) 范围的序列合并成一个有序序列 */
private void merge(int begin, int mid, int end) {
int li = 0, le = mid - begin;
int ri = mid, re = end;
int ai = begin;
//备份左边数组
for (int i = 0; i < le; i++) {
leftArr[i] = array[begin + i];
}
//如果左边还没有结束(情况一)
while (li < le) {
//当 ri < re 不成立,就会一直leftArr挪动(情况二)
if (ri < re && cmp(array[ri],leftArr[li]) < 0) {
array[ai++] = array[ri++];
} else { //注意稳定性
array[ai++] = leftArr[li++];
}
}
}
}
7.4 算法优劣

复杂度分析
T(n) = sort() + sort() + merge()
=> T(n) = T(n/2) + T(n/2) + O(n)
=> T(n) = 2T(n/2) + O(n)
//由于sort()是递归调用,用T表示,由于T(n/2)不好估算,现在要理清T(n)与O(n)之间的关系
T(1) = O(1)
T(n)/n = T(n/2) / (n/2) + O(1)
//令S(n) = T(n)/n
S(1) = O(1)
S(n) = S(n/2) + O(1)
= S(n/4) + O(2)
= S(n/8) + O(3)
= S( n/(2^k) ) + O(k)
= S(1) + O(log^n)
= O(lon^n)
T(n) = n*S(n) = O(nlog^n)
=> 归并排序时间复杂度:O(nlog^n)
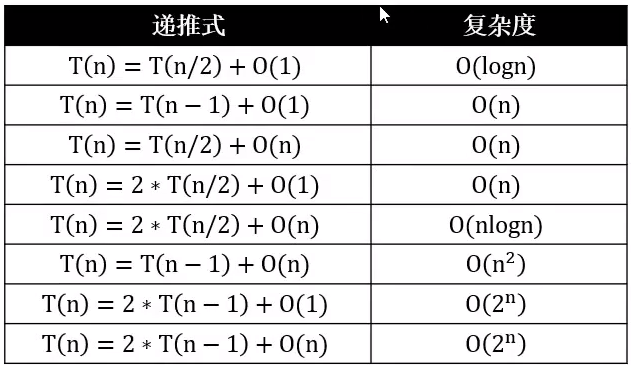
常见递推式
总结











