Hash3(Leslie)=5
通过上面的元素,可以知道此时 0,4,5 这三个位置上都是 1。
布隆过滤器就会觉得这个元素之前可能出现过。于是就会返回给调用者:[Leslie]曾经出现过。
但是实际情况呢?
其实我们心里门清,[Leslie] 不曾来过。
这就是误报的情况。
这就是前面说的:布隆过滤器说存在的元素,不一定存在。
而一个元素经过某个 hash 计算后,如果对应位置上的值是 0,那么说明该元素一定不存在。
但是它有一个致命的缺点,就是不支持删除。
为什么?
假设要删除 [why],那么就要把 1,4,8 这三个位置置为 0。
但是你想啊,[jay] 也指向了位置 8 呀。
如果删除 [why] ,位置 8 变成了 0,那么是不是相当于把 [jay] 也移除了?

为什么不支持删除就致命了呢?
你又想啊,本来布隆过滤器就是使用于大数据量的场景下,随着时间的流逝,这个过滤器的数组中为 1 的位置越来越多,带来的结果就是误判率的提升。从而必须得进行重建。
所以,文章开始举的腾讯的例子中有这样一句话:

除了删除这个问题之外,布隆过滤器还有一个问题:查询性能不高。
因为真实场景中过滤器中的数组长度是非常长的,经过多个不同 Hash 函数后,得到的数组下标在内存中的跨度可能会非常的大。跨度大,就是不连续。不连续,就会导致 CPU 缓存行命中率低。
这玩意,这么说呢。就当八股文背起来吧。
踏雪留痕,雁过留声,这就是布隆过滤器。
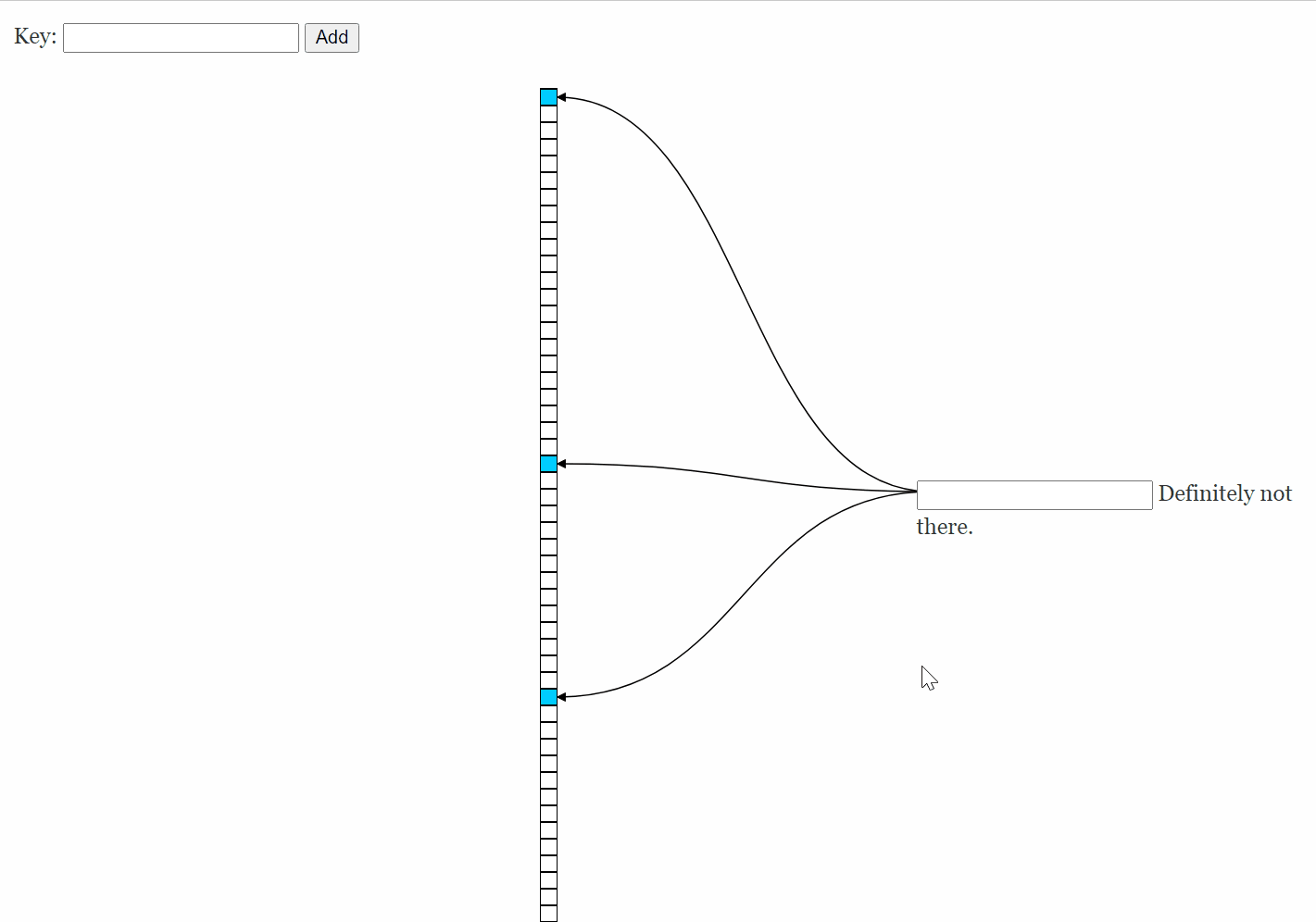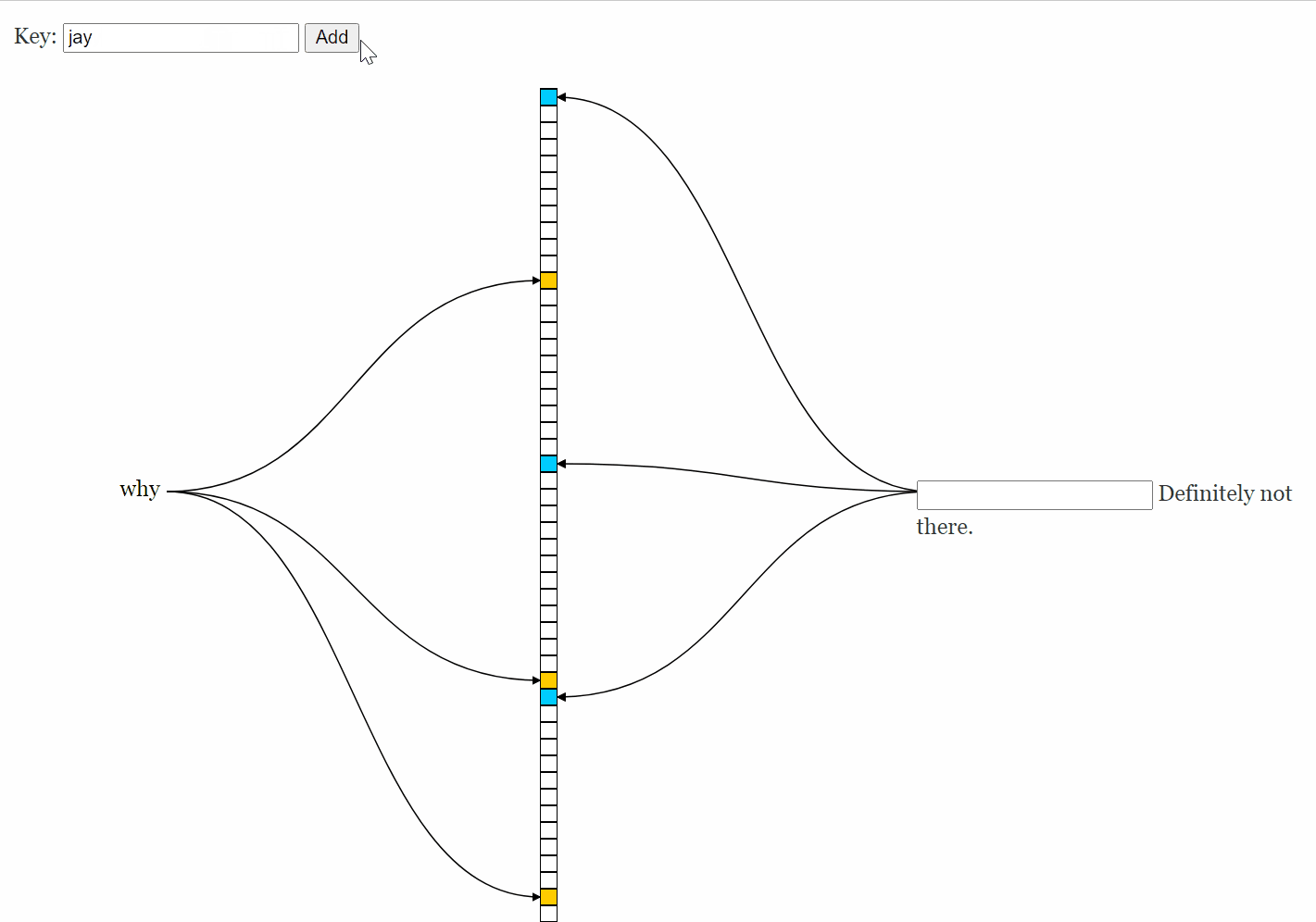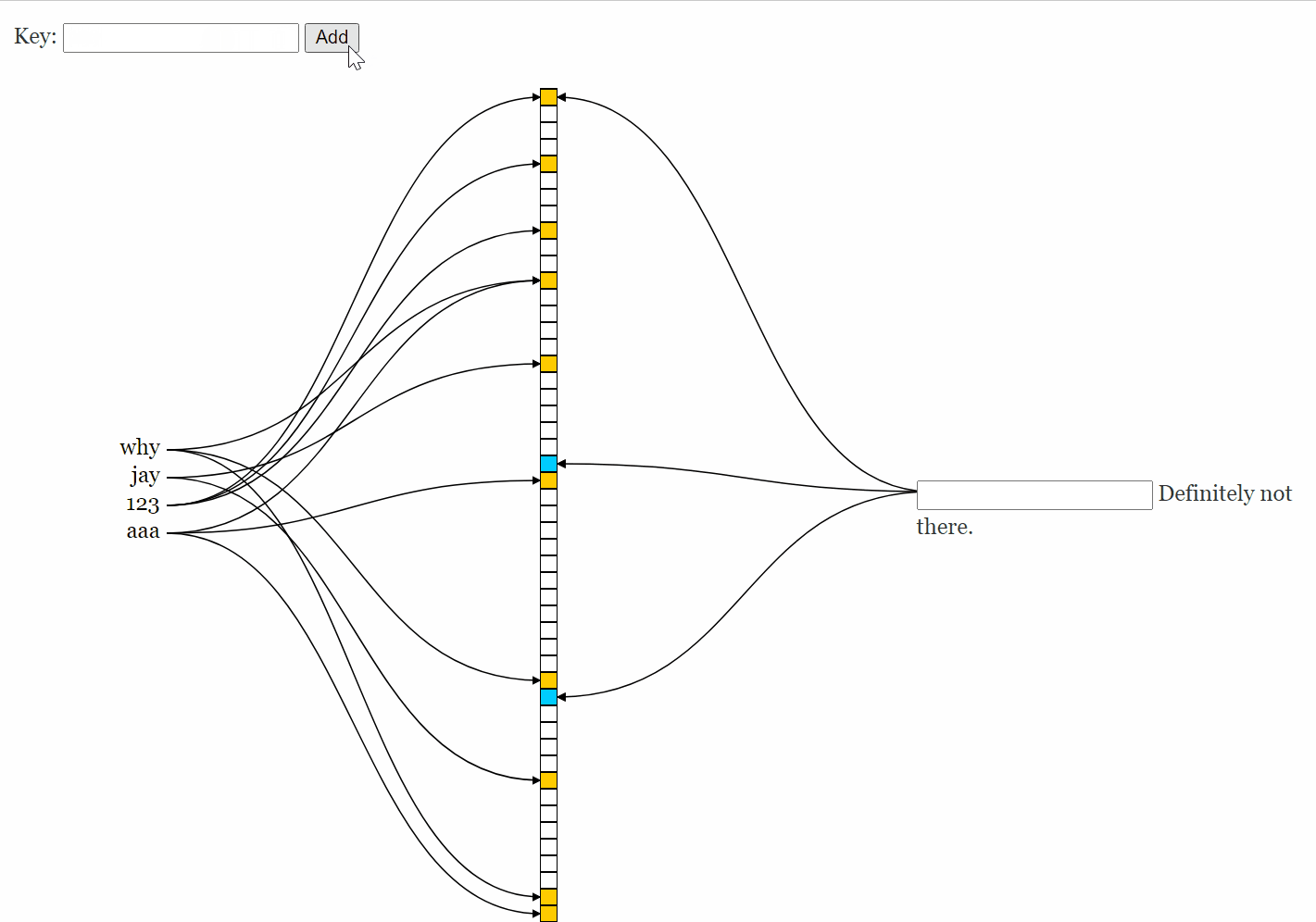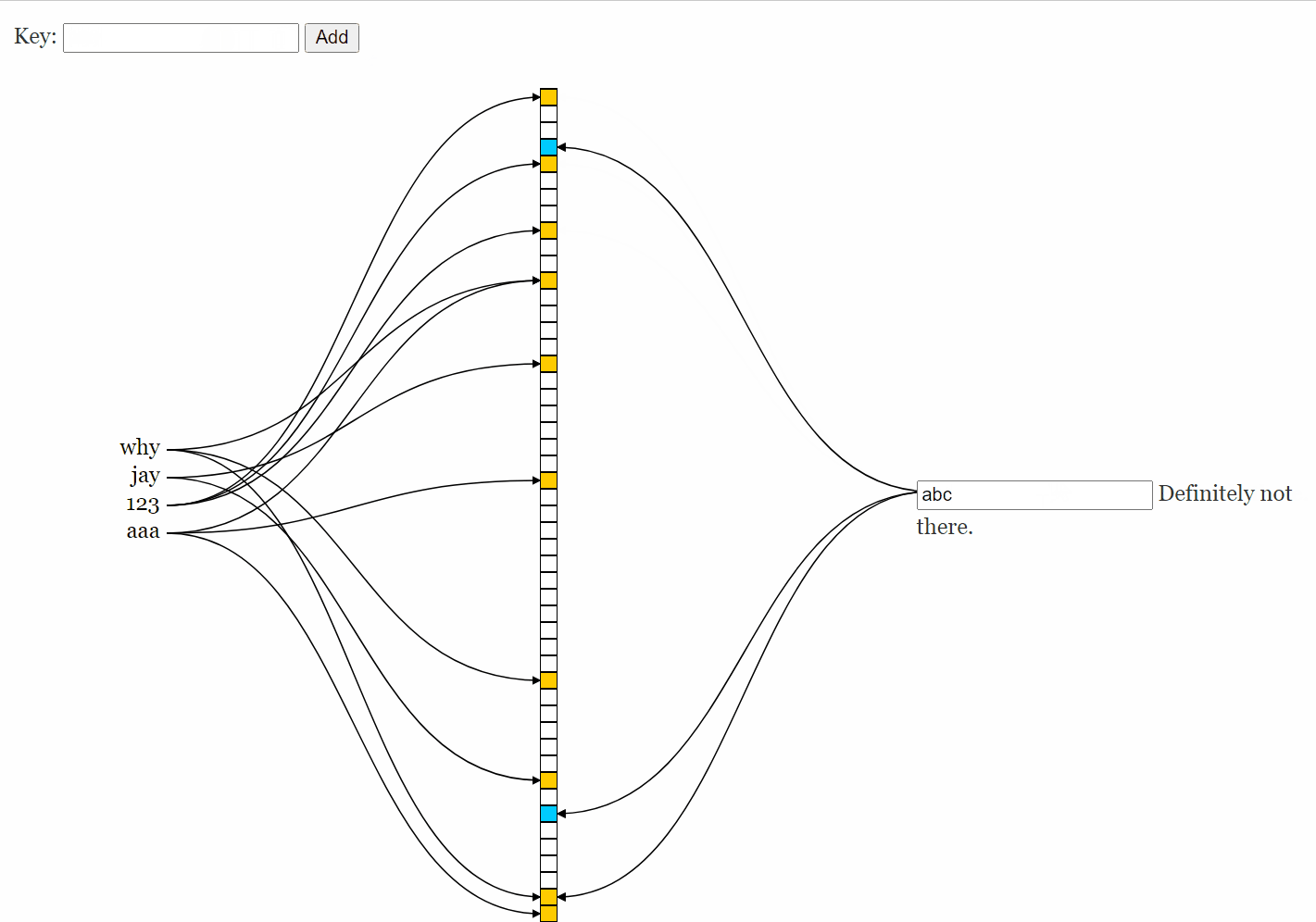
如果你想玩一下布隆过滤器,可以访问一下这个网站:
https://www.jasondavies.com/bloomfilter/
左边插入,右边查询:
如果要布隆过滤器支持删除,那么怎么办呢?
有一个叫做 Counting Bloom Filter。
它用一个 counter 数组,替换数组的比特位,这样一比特的空间就被扩大成了一个计数器。
用多占用几倍的存储空间的代价,给 Bloom Filter 增加了删除操作。
这也是一个解决方案。
但是还有更好的解决方案,那就是布谷鸟过滤器。
另外,关于布隆过滤器的误判率,有一个数学推理公式。很复杂,很枯燥,就不讲了,有兴趣的可以去了解一下。
~cao/papers/summary-cache/node8.html
布谷鸟 hash布谷鸟过滤器,第一次出现是在 2014 年发布的一篇论文里面:《Cuckoo Filter: Practically Better Than Bloom》
https://www.cs.cmu.edu/~dga/papers/cuckoo-conext2014.pdf

但是在讲布谷鸟过滤器之前,得简单的铺垫一下 Cuckoo hashing,也就是布谷鸟 hash 的知识。
因为这个词是论文的关键词,在文中出现了 52 次之多。
Cuckoo hashing,最早出现在这篇 2001 年的论文之中:
https://www.cs.tau.ac.il/~shanir/advanced-seminar-data-structures-2009/bib/pagh01cuckoo.pdf
主要看论文的这个地方:

它的工作原理,总结起来是这样的:
它有两个 hash 表,记为 T1,T2。
两个 hash 函数,记为 h1,h2。
当一个不存在的元素插入的时候,会先根据 h1 计算出其在 T1 表的位置,如果该位置为空则可以放进去。
如果该位置不为空,则根据 h2 计算出其在 T2 表的位置,如果该位置为空则可以放进去。
如果该位置不为空,就把当前位置上的元素踢出去,然后把当前元素放进去就行了。
也可以随机踢出两个位置中的一个,总之会有一个元素被踢出去。
被踢出去的元素怎么办呢?

没事啊,它也有自己的另外一个位置。
论文中的伪代码是这样的:

看不懂没关系,我们画个示意图:
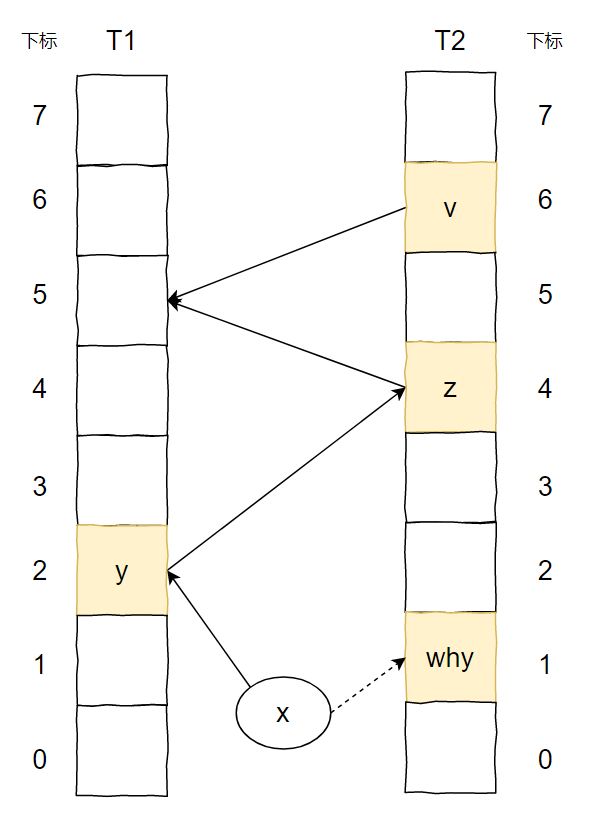
上面的图说的是这样的一个事儿:
我想要插入元素 x,经过两个 hash 函数计算后,它的两个位置分别为 T1 表的 2 号位置和 T2 表的 1 号位置。
两个位置都被占了,那就随机把 T1 表 2 号位置上的 y 踢出去吧。
而 y 的另一个位置被 z 元素占领了。
于是 y 毫不留情把 z 也踢了出去。
z 发现自己的备用位置还空着(虽然这个备用位置也是元素 v 的备用位置),赶紧就位。
所以,当 x 插入之后,图就变成了这样:
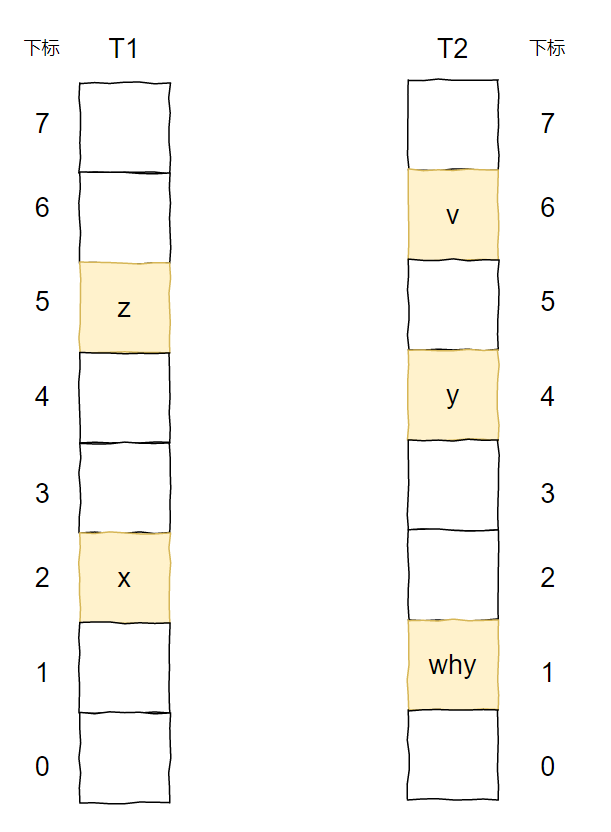
上面这个图其实来源就是论文里面:
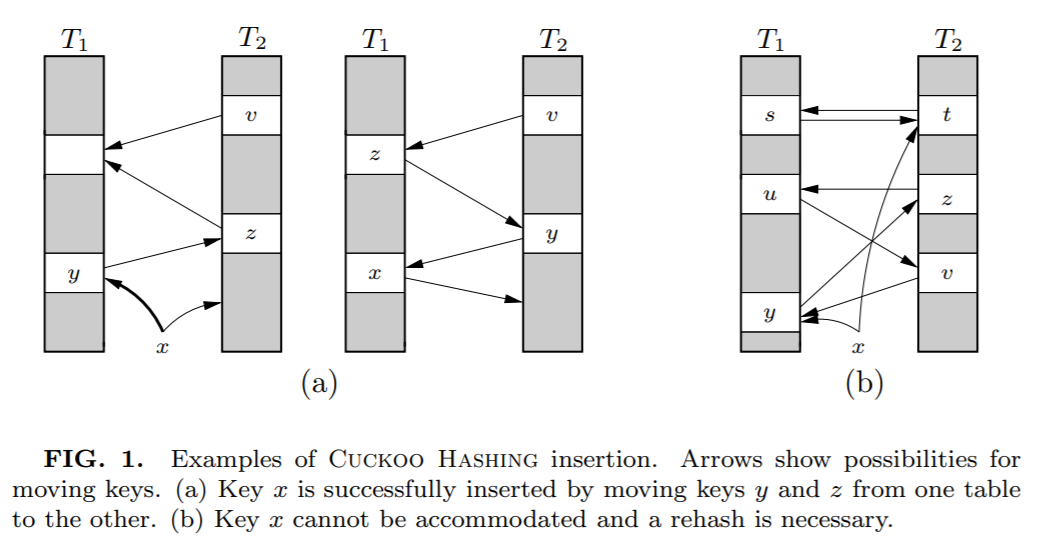
这种类似于套娃的解决方式看是可行,但是总是有出现循环踢出导致放不进 x 的问题。
比如上图中的(b)。
当遇到这种情况时候,说明布谷鸟 hash 已经到了极限情况,应该进行扩容,或者 hash 函数的优化。
所以,你再次去看伪代码的时候,你会明白里面的 MaxLoop 的含义是什么了。
这个 MaxLoop 的含义就是为了避免相互踢出的这个过程执行次数太多,设置的一个阈值。
其实我理解,布谷鸟 hash 是一种解决 hash 冲突的骚操作。
如果你想上手玩一下,可以访问这个网站:
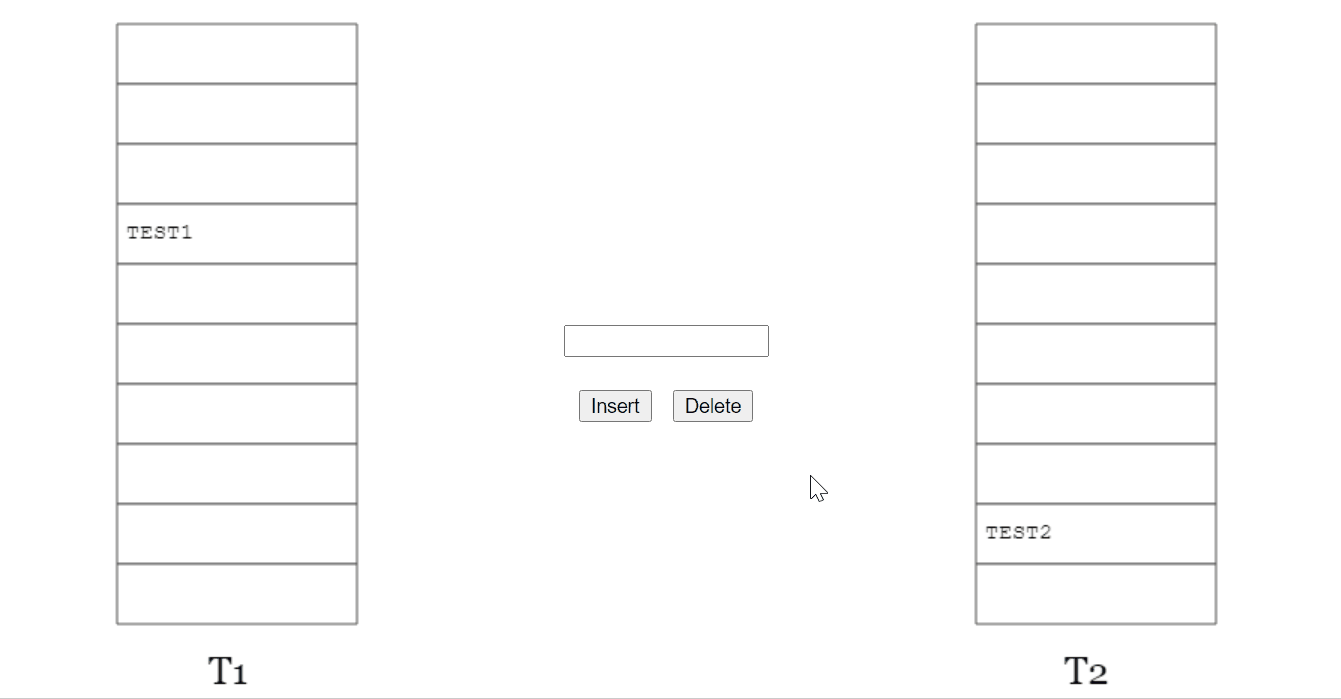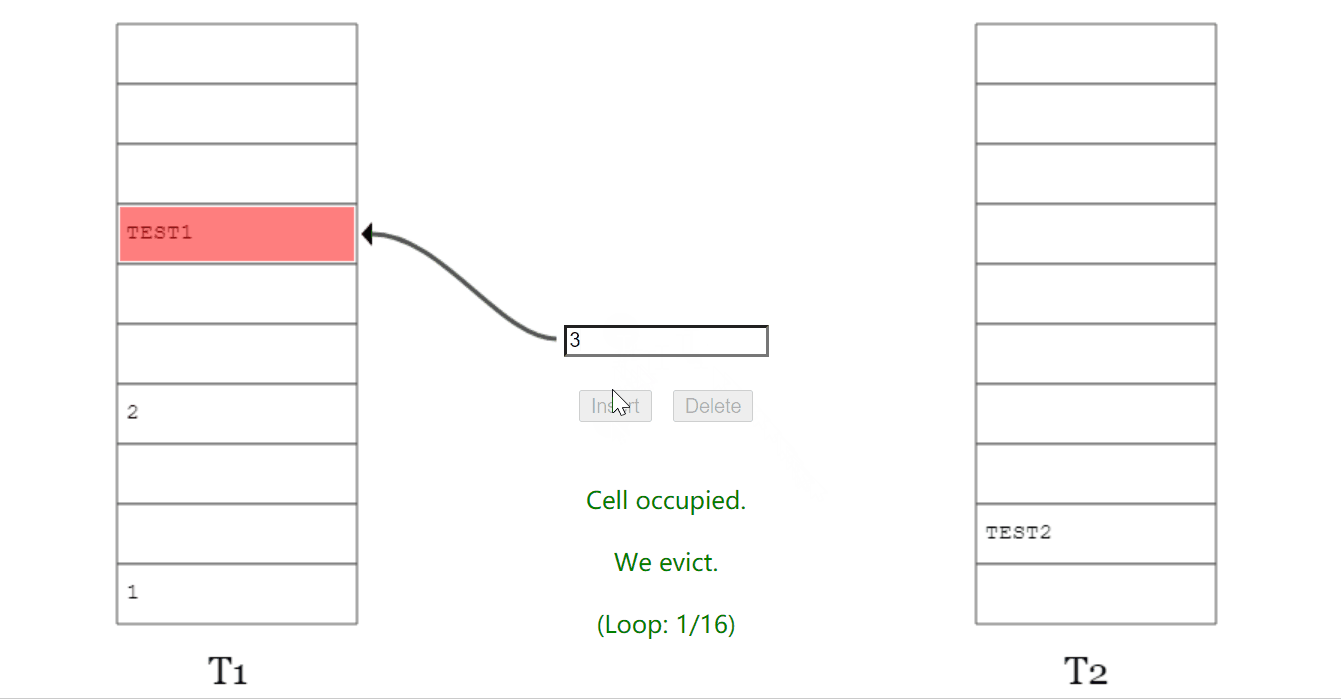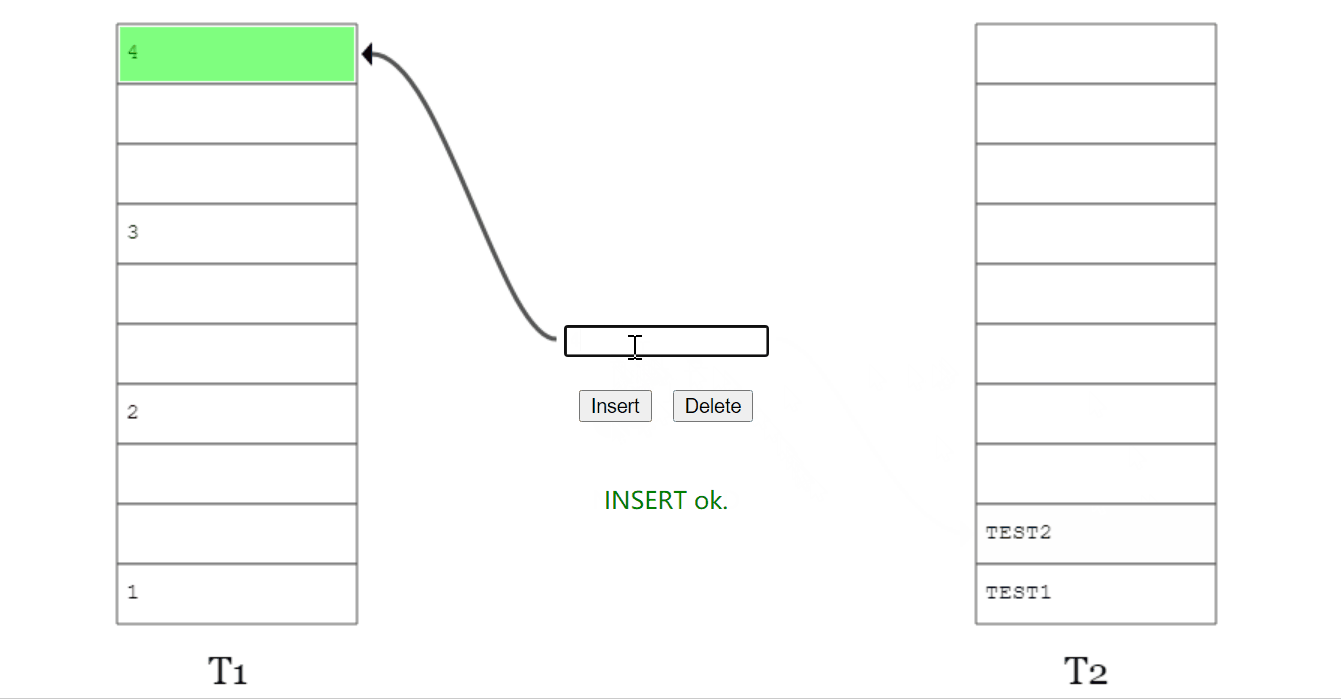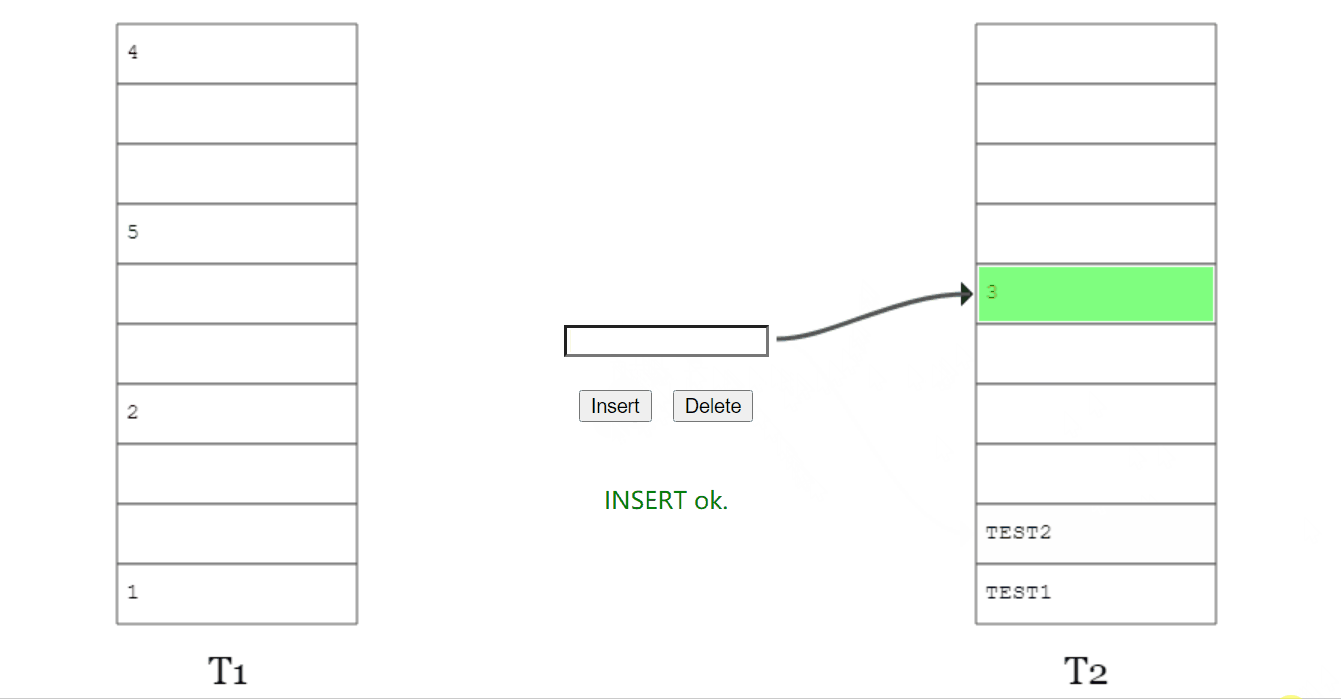
当踢来踢去了 16 (MaxLoop)次还没插入完成后,它会告诉你,需要 rehash 并对数组扩容了:
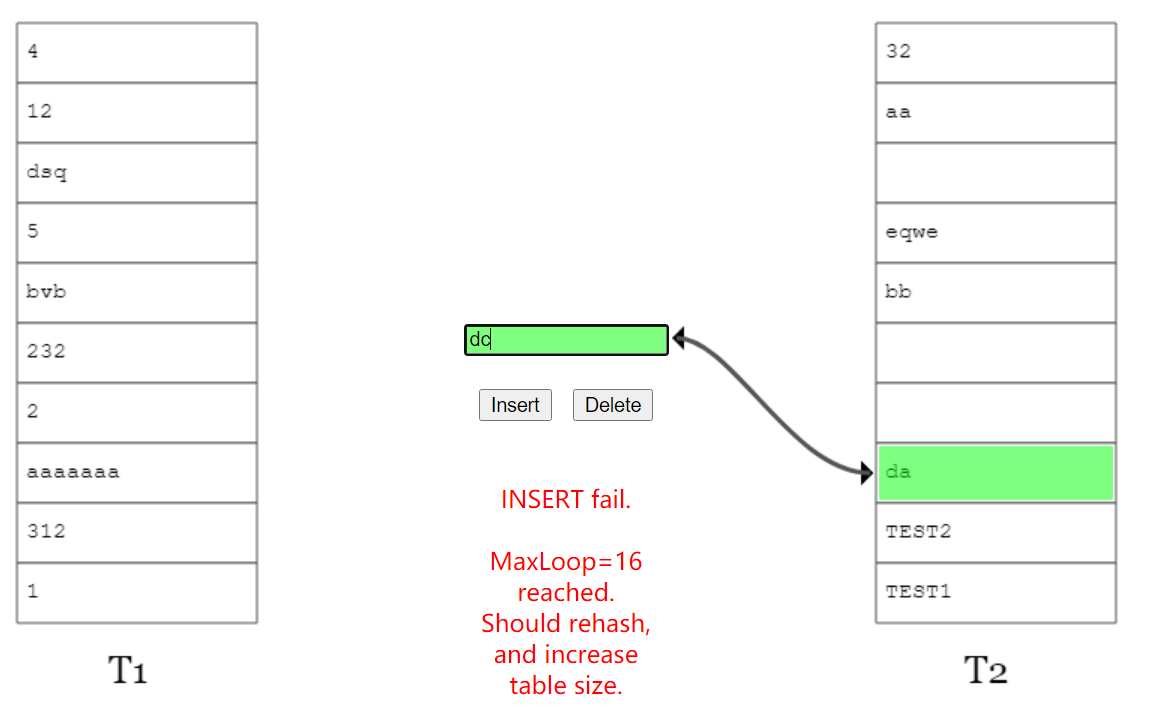
布谷鸟 hash 就是这么一回事。
接着,我们看布谷鸟过滤器。
布谷鸟过滤器布谷鸟过滤器的论文《Cuckoo Filter: Practically Better Than Bloom》开篇第一页,里面有这样一段话。
直接和布隆过滤器正面刚:我布谷鸟过滤器,就是比你屌一点。
上来就指着别人的软肋怼:

标准的布隆过滤器的一大限制是不能删除已经存在的数据。如果使用它的变种,比如 Counting Bloom Filter,但是空间却被撑大了 3 到 4 倍,巴拉巴拉巴拉......
而我就不一样了:

这篇论文将要证明的是,与标准布隆过滤器相比,支持删除并不需要在空间或性能上提出更高的开销。
布谷鸟过滤器是一个实用的数据结构,提供了四大优势:
1.支持动态的新增和删除元素。
2.提供了比传统布隆过滤器更高的查找性能,即使在接近满的情况下(比如空间利用率达到 95% 的时候)。
3.比诸如商过滤器(quotient filter,另一种过滤器)之类的替代方案更容易实现。

