布谷鸟过滤器:我烦死了,TMD!
接下来,说一下“指纹”。

这是论文中第一次出现“指纹”的地方。
“指纹”其实就是插入的元素进行一个 hash 计算,而 hash 计算的产物就是 几个 bit 位。
布谷鸟过滤器里面存储的就是元素的“指纹”。
查询数据的时候,就是看看对应的位置上有没有对应的“指纹”信息:
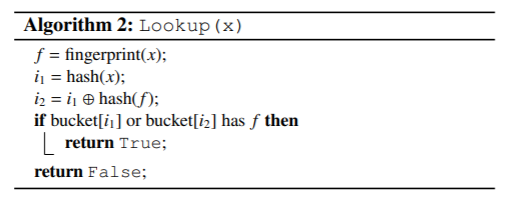
删除数据的时候,也只是抹掉该位置上的“指纹”而已:

由于是对元素进行 hash 计算,那么必然会出现“指纹”相同的情况,也就是会出现误判的情况。
没有存储原数据,所以牺牲了数据的准确性,但是只保存了几个 bit,因此提升了空间效率。
说到空间利用率,你想想布谷鸟 hash 的空间利用率是多少?
在完美的情况下,也就是没有发生哈希冲突之前,它的空间利用率最高只有 50%。
因为没有发生冲突,说明至少有一半的位置是空着的。
除了只存储“指纹”,布谷鸟过滤器还能怎么提高它的空间利用率的呢?
看看论文里面怎么说的:
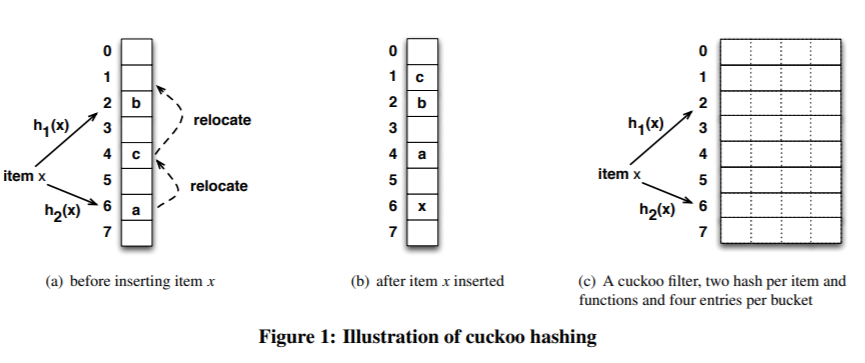
前面的(a)、(b)很简单,还是两个 hash 函数,但是没有用两个数组来存数据,就是基于一维数组的布谷鸟 hash ,核心还是踢来踢去,不多说了。
重点在于(c),对数组进行了展开,从一维变成了二维。
每一个下标,可以放 4 个元素了。
这样一个小小的转变,空间利用率从 50% 直接到了 98%:

我就问你怕不怕?
上面截图的论文中的第一点就是在陈诉这样一个事实:
当 hash 函数固定为 2 个的时候,如果一个下标只能放一个元素,那么空间利用率是 50%。
但是如果一个下标可以放 2,4,8 个元素的时候,空间利用率就会飙升到 84%,95%,98%。
到这里,我们明白了布谷鸟过滤器对布谷鸟 hash 的优化点和对应的工作原理。
看起来一切都是这么的完美。
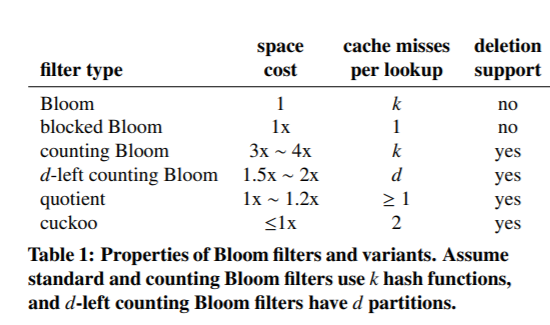
各项指标都比布隆过滤器好,主打的是支持删除的操作。
但是真的这么好吗?
当我看到论文第六节的这一段的时候,沉默了:

对重复数据进行限制:如果需要布谷鸟过滤器支持删除,它必须知道一个数据插入过多少次。不能让同一个数据插入 kb+1 次。其中 k 是 hash 函数的个数,b 是一个下标的位置能放几个元素。
比如 2 个 hash 函数,一个二维数组,它的每个下标最多可以插入 4 个元素。那么对于同一个元素,最多支持插入 8 次。
例如下面这种情况:
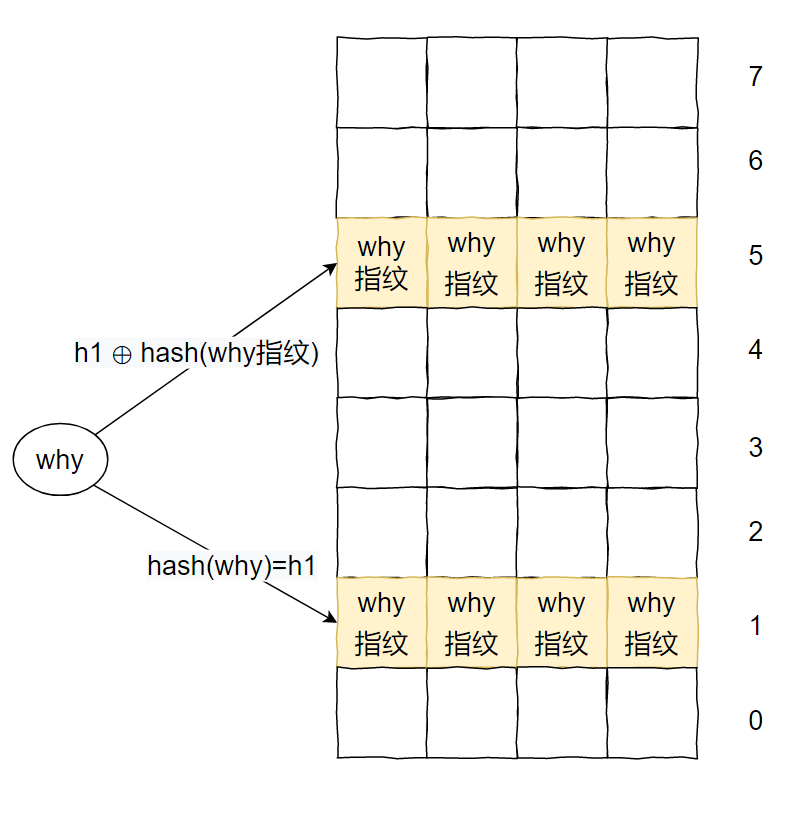
why 已经插入了 8 次了,如果再次插入一个 why,则会出现循环踢出的问题,直到最大循环次数,然后返回一个 false。
怎么避免这个问题呢?
我们维护一个记录表,记录每个元素插入的次数就行了。
虽然逻辑简单,但是架不住数据量大呀。你想想,这个表的存储空间又怎么算呢?
想想就难受。
如果你要用布谷鸟过滤器的删除操作,那么这份难受,你不得不承受。
最后,再看一下各个类型的过滤器的对比图吧:
还有,其中的数学推理过程,不说了,看的眼睛疼,而且看这玩意容易掉头发。
你知道为什么叫做“布谷鸟”吗?
布谷鸟,又叫杜鹃。

