文章图片来源于 GitHub,网速不佳的朋友,请看《堆、堆排序和优先队列的那些事》 或者 来我的技术小站 godbmw.com
1. 什么是堆?堆是一种数据结构,它是一颗完全二叉树。
堆分为最大堆和最小堆:
最大堆:任意节点的值不大于其父亲节点的值。
最小堆:任意节点的值不小于其父亲节点的值。
如下图所示,就是个最大堆:

注:本文中的代码实现是最大堆,最小堆的实现相似,不再冗赘。
2. 堆有什么用途?堆最常用于优先队列以及相关动态问题。
优先队列指的是元素入队和出队的顺序与时间无关,既不是先进先出,也不是先进后出,而是根据元素的重要性来决定的。
例如,操作系统的任务执行是优先队列。一些情况下,会有新的任务进入,并且之前任务的重要性也会改变或者之前的任务被完成出队。而这个出队、入队的过程利用堆结构,时间复杂度是O(log2_n)。

堆中的元素存储,一般是借用一个数组:这个数组是从 1 开始计算的。更方便子节点和父节点的表示。

入堆即向堆中添加新的元素,然后将元素移动到合适的位置,以保证堆的性质。
在入堆的时候,需要shift_up操作,如下图所示:
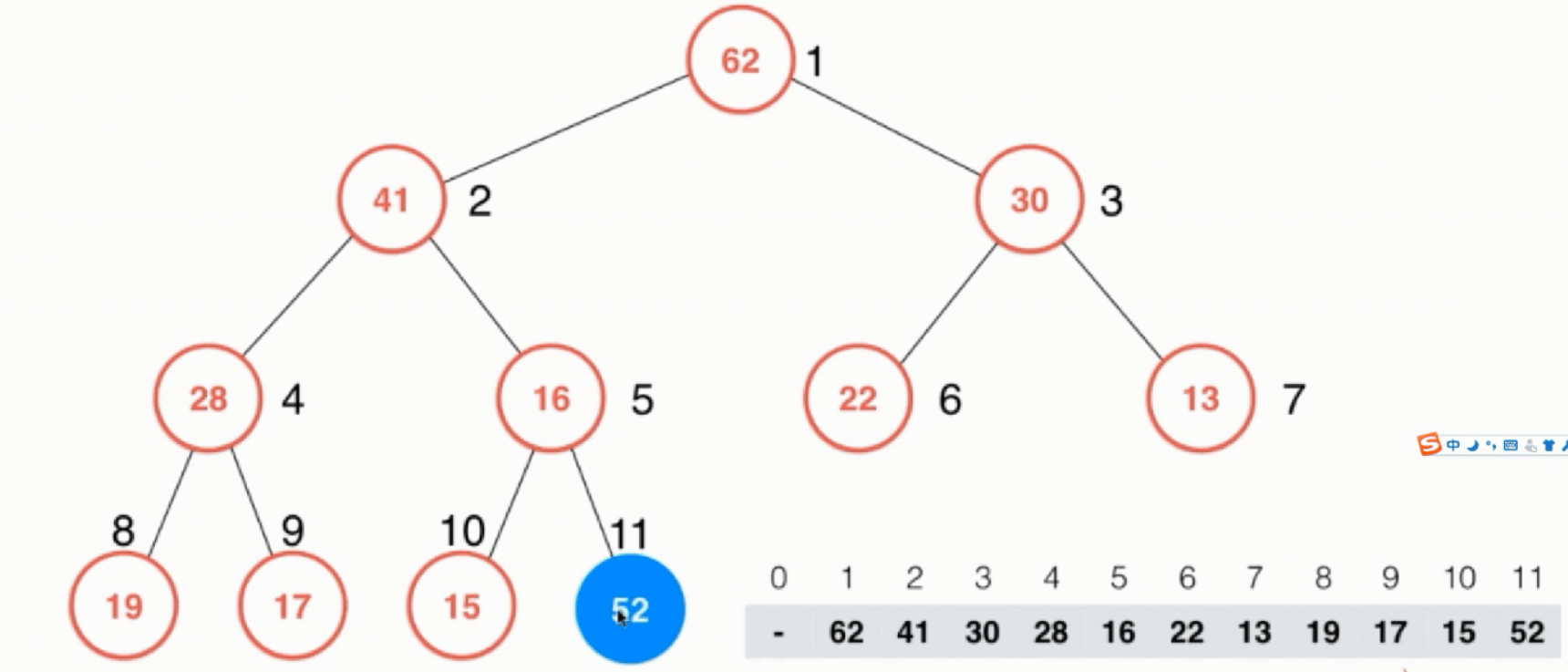
插入 52 元素后,不停将元素和上方父亲元素比较,如果大于,则交换元素;直到达到堆顶或者小于等于父亲元素。
3.3 出堆出堆只能弹出堆顶元素(最大堆就是最大的元素),调整元素为止保证堆的性质。
在入堆的时候,需要shift_down操作,如下图所示:

已经取出了堆顶元素,然后将位于最后一个位置的元素放入堆顶(图中是16被放入堆顶)。
重新调整元素位置。此时元素应该和子节点比较,如果大于等于子节点或者没有子节点,停止比较;否则,选择子节点中最大的元素,进行交换,执行此步,直到结束。
3.4 实现优化在优化的时候,有两个部分需要做:
swap操作应该被替换为:单次赋值,减少赋值次数
入堆操作:空间不够的时候,应该开辟 2 倍空间,防止数组溢出
3.5 代码实现 // MaxHeap.h // Created by godbmw.com on 2018/9/19. // #ifndef MAXHEAP_MAXHEAP_H #define MAXHEAP_MAXHEAP_H #include <iostream> #include <algorithm> #include <cassert> #include <typeinfo> using namespace std; template <typename Item> class MaxHeap { private: Item* data; // 堆数据存放 int count; // 堆目前所含数据量大小 int capacity; // 堆容量大小 void shift_up(int k) { Item new_item = this->data[k]; // 保存新插入的值 // 如果新插入的值比父节点的值小, 则父节点的值下移, 依次类推, 直到到达根节点或者满足最大堆定义 while( k > 1 && this->data[k/2] < new_item ) { this->data[k] = this->data[k/2]; k /= 2; } this->data[k] = new_item; // k就是 新插入元素 应该在堆中的位置 } void shift_down(int k) { Item root = this->data[1]; // 在完全二叉树中判断是否有左孩子即可 while(2*k <= this->count) { int j = k + k; // 如果有右子节点,并且右节点 > 左边点 if( j + 1 <= this->count && this->data[j + 1] > this->data[j]) { j += 1; } // root找到了堆中正确位置 k 满足堆性质, 跳出循环 if(root >= this->data[j]) { break; } this->data[k] = this->data[j]; k = j; } this->data[k] = root; } public: MaxHeap(int capacity) { this->data = new Item[capacity + 1]; // 堆中数据从索引为1的位置开始存储 this->count = 0; this->capacity = capacity; } // 将数组构造成堆:heapify MaxHeap(Item arr[], int n) { this->data = new Item[n+1]; this->capacity = n; this->count = n; for(int i = 0; i < n; i++) { this->data[i + 1] = arr[i]; } for(int i = n/2; i >= 1; i--) { this->shift_down(i); } } ~MaxHeap(){ delete[] this->data; } // 返回堆中元素个数 int size() { return this->count; } // 返回布尔值:堆中是否为空 bool is_empty() { return this->count == 0; } // 向堆中插入元素 void insert(Item item) { // 堆空间已满, 开辟新的堆空间. // 按照惯例,容量扩大到原来的2倍 if(this->count >= this->capacity) { this->capacity = this->capacity + this->capacity; // 容量变成2倍 Item* more_data = new Item[this->capacity + 1]; // data[0] 不存放任何元素 copy(this->data, this->data + this->count + 1, more_data); // 将原先 data 中的有效数据拷贝到 more_data 中 delete[] this->data; this->data = more_data; } this->data[this->count + 1] = item; // 插入堆尾部 this->shift_up(this->count + 1); // 执行 shift_up,将新插入的元素移动到应该在的位置 this->count ++; } // 取出最大值 Item extract_max() { assert(this->count > 0); Item ret = this->data[1]; // 取出根节点 swap(this->data[1], this->data[this->count]); // 将根节点元素和最后元素交换 this->count --; // 删除最后一个元素 this->shift_down(1); // shift_down 将元素放到应该在的位置 return ret; } }; #endif //MAXHEAP_MAXHEAP_H 4. 堆排序
