索引是数据库常见的数据结构,每个后台开发人员都应该对索引背后的数据结构有所了解。
本文通过分析B-Tree及B-/+Tree数据结构及索引性能分析及磁盘存取原理尝试着回答一下问题:
为什么B-Tree适合数据库索引及红黑树的二叉平衡树不适合作为索引
B+Tree比BTree做索引的优势
为什么MongoDB采用B-Tree作为索引结构而MySQL采用B+Tree作为索引存储结构
B-TreeB 树(B-Tree)是为磁盘等辅助存取设备设计的一种平衡查找树,它实现了以 \(O(\lg n)\) 时间复杂度执行查找、顺序读取、插入和删除操作。由于 B 树和 B 树的变种在降低磁盘 I/O 操作次数方面表现优异,所以经常用于设计文件系统和数据库。
使用阶来定义 B 树,一棵 m 阶的 B 树,需要满足下列条件:
每个节点最多拥有m个子节点且m>=2,空树除外
除根节点外每个节点的关键字数量大于等于ceil(m/2)-1,小于等于m-1,非根节点关键字数必须>=2
所有叶子节点均在同一层、叶子节点除了包含了关键字和关键字记录的指针外也有指向其子节点的指针只不过其指针地址都为null对应下图最后一层节点的空格子
如果一个非叶节点有n个子节点,则该节点的关键字数等于n-1
所有节点关键字是按递增次序排列,并遵循左小右大原则
注:
m阶代表一个树节点最多有多少个查找路径,m阶=m路,当m=2则是2叉树,m=3则是3叉。
ceil()是个朝正无穷方向取整的函数,如ceil(1.1)结果为2,即向上取整。
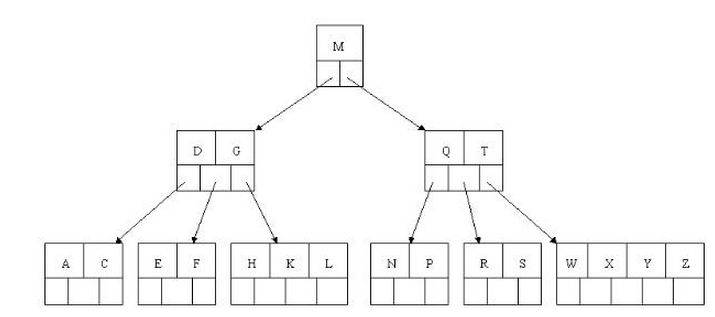
B 树中的节点分为内部节点(Internal Node)和叶节点(Leaf Node),内部节点也就是非叶节点(Non-Leaf Node)。
B-Tree的查找B-Tree的查找过程:根据给定值查找结点和在结点的关键字中进行查找交叉进行。
首先从根结点开始重复如下过程:若比结点的第一个关键字小,则查找在该结点第一个指针指向的结点进行;若等于结点中某个关键字,则查找成功;若在两个关键字之间,则查找在它们之间的指针指向的结点进行;若比该结点所有关键字大,则查找在该结点最后一个指针指向的结点进行;若查找已经到达某个叶结点,则说明给定值对应的数据记录不存在,查找失败。
例如:
在一棵 5 阶B-树中查找元素 29
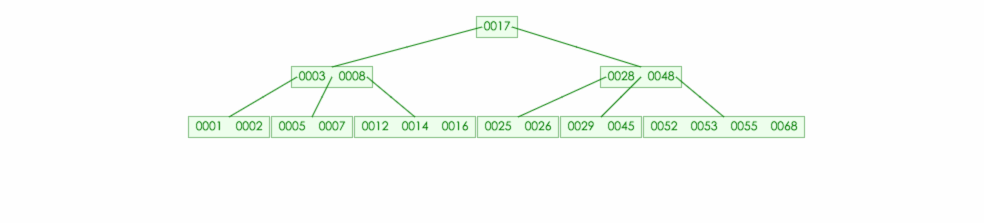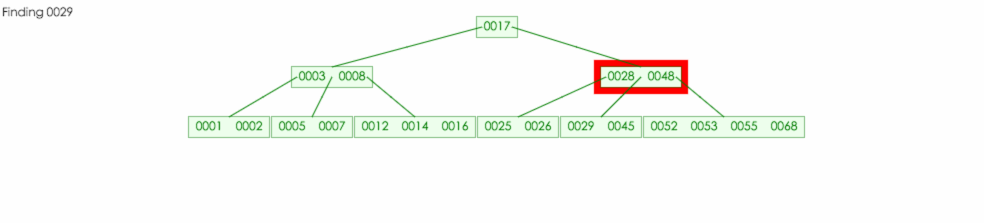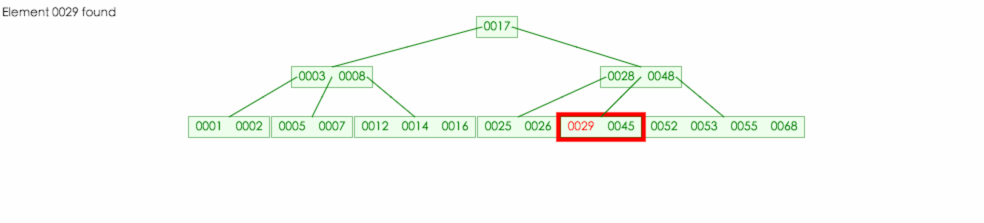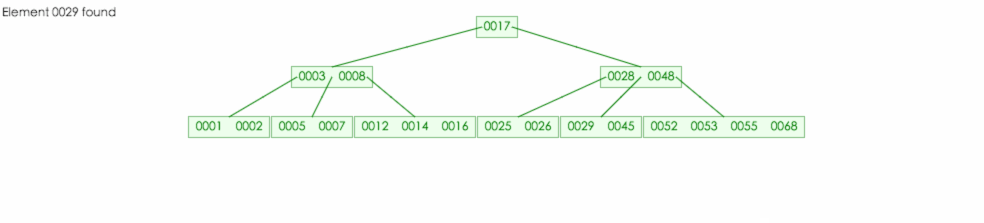
首先29比根节点值大,所以找根节点的右子数,然后再根据值得判断,发现 29 介于 28 和 48 之间,然后在从中间子树继续查找下去。
B-Tree的插入插入的过程分两步完成:
利用前述的B-树的查找算法查找关键字的插入位置。若找到,则说明该关键字已经存在,直接返回。否则查找操作必失败于某个最低层的非终端结点上。
判断该结点是否还有空位置。即判断该结点的关键字总数是否满足n<=m-1。若满足,则说明该结点还有空位置,直接把关键字k插入到该结点的合适位置上。若不满足,说明该结点己没有空位置,需要把结点分裂成两个。
分裂的方法是:
生成一新结点。把原结点上的关键字和k按升序排序后,从中间位置把关键字(不包括中间位置的关键字)分成两部分。左部分所含关键字放在旧结点中,右部分所含关键字放在新结点中,中间位置的关键字连同新结点的存储位置插入到父结点中。如果父结点的关键字个数也超过(m-1),则要再分裂,再往上插。直至这个过程传到根结点为止。
例子:
如果该节点的元素个数还没达到 m,则插入完后无需处理
比如:

如果该节点元素个数达到 m 时,这时候将元素插入到合适的位置,将最中间的元素取出,成为该节点的父节点元素,然后将其余左右元素拆成两个新节点
比如:

刚才的操作可能导致父节点的元素个数达到 m,这时候用情况 2 迭代处理,直到如果遇到根结点元素个数达到 m,则最中间元素将成为新的根结点。
比如:

我们需要分两种情况进行讨论:
如果该元素存在于叶子结点,直接删除它,无需进行其它处理。

