与解法一相同的是,解法二也借助于两个队列。不同之处在于解法二在入栈时,已经在队列中将元素排列成出栈的顺序。因此,解法二实现的栈的入栈操作是 \(O(n)\) 的时间复杂度,而出栈操作则只需要 \(O(1)\) 的时间复杂度。相关操作的底层实现细节见下面对应的小节。
入栈(push)为了使得队列1 q1 中的出队顺序和出栈顺序是一致的,需要借助另一个队列(辅助队列 q2)。每次有新的元素压入栈时,将该元素入队到队列2 q2 中。接着,将队列1 q1 中的所有元素出队并入队到队列2 q2 中。最后,再将两个队列的引用进行交换,则队列1 q1 中出队的顺序即为实际的出栈顺序。具体的操作步骤如图3所示。
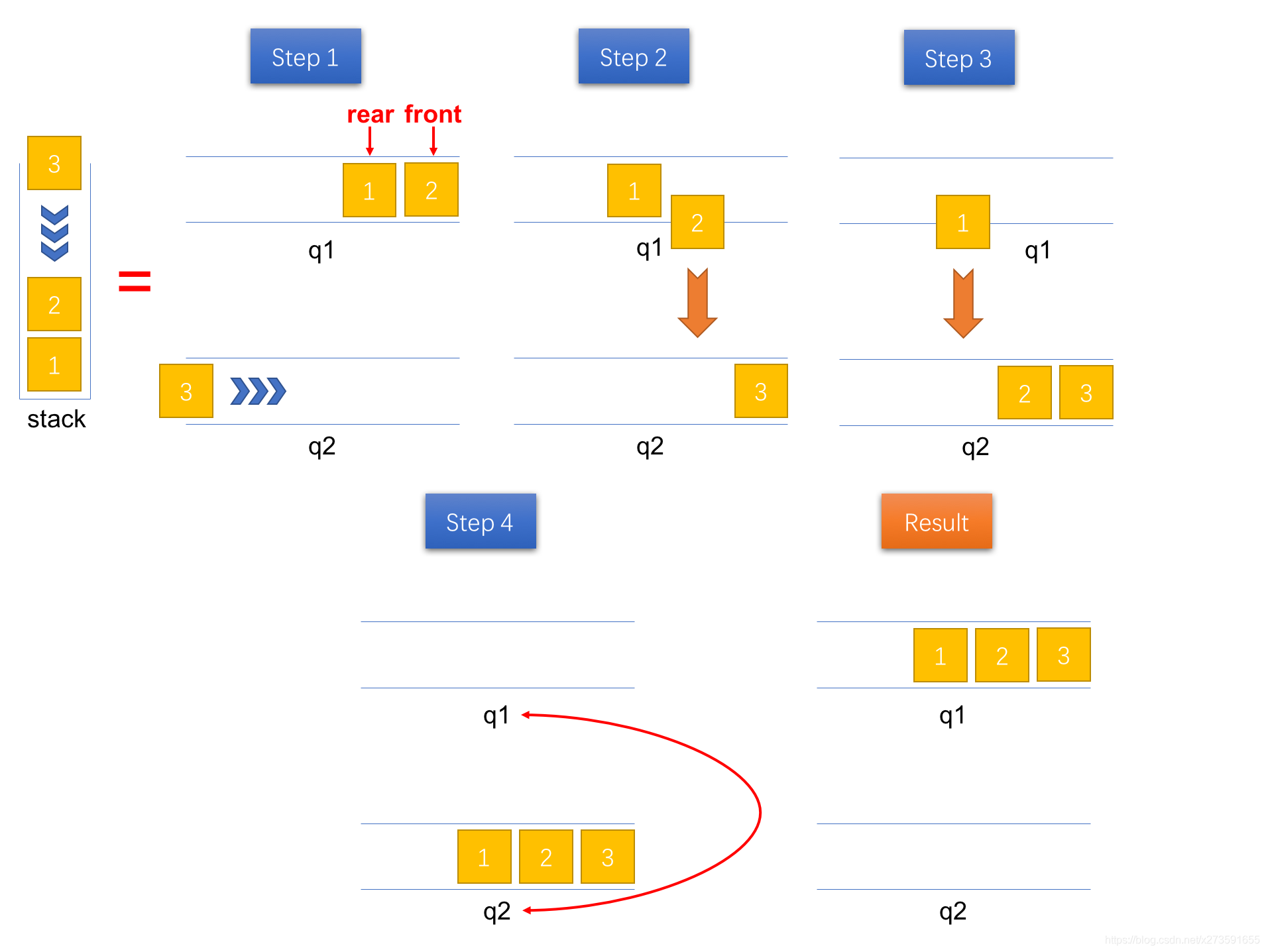
图3:将一个元素压入栈
代码(Java)实现如下:
/** Push element x onto stack. */ public void push(int x) { q2.add(x); while (!q1.isEmpty()) { q2.add(q1.remove()); } Queue<Integer> temp = q1; q1 = q2; q2 = temp; }复杂度分析如下:
时间复杂度:\(O(n)\),其中 \(n\) 表示入栈前元素的数目。入栈操作需要 \(n+1\) 个入队操作,同时还需要 \(n\) 个出队操作,因此,总共需要 \(2n + 1\) 个操作。由于 LinkedList 的添加和删除操作的时间复杂度是 \(O(1)\) 的,因此,总的时间复杂度是 \(O(n)\) 的
空间复杂度:\(O(1)\)
出栈(pop)由于在入栈时已经将队列中的元素排列成出栈的顺序,因此,只需要出队队列1 q1 中队首的元素即可。
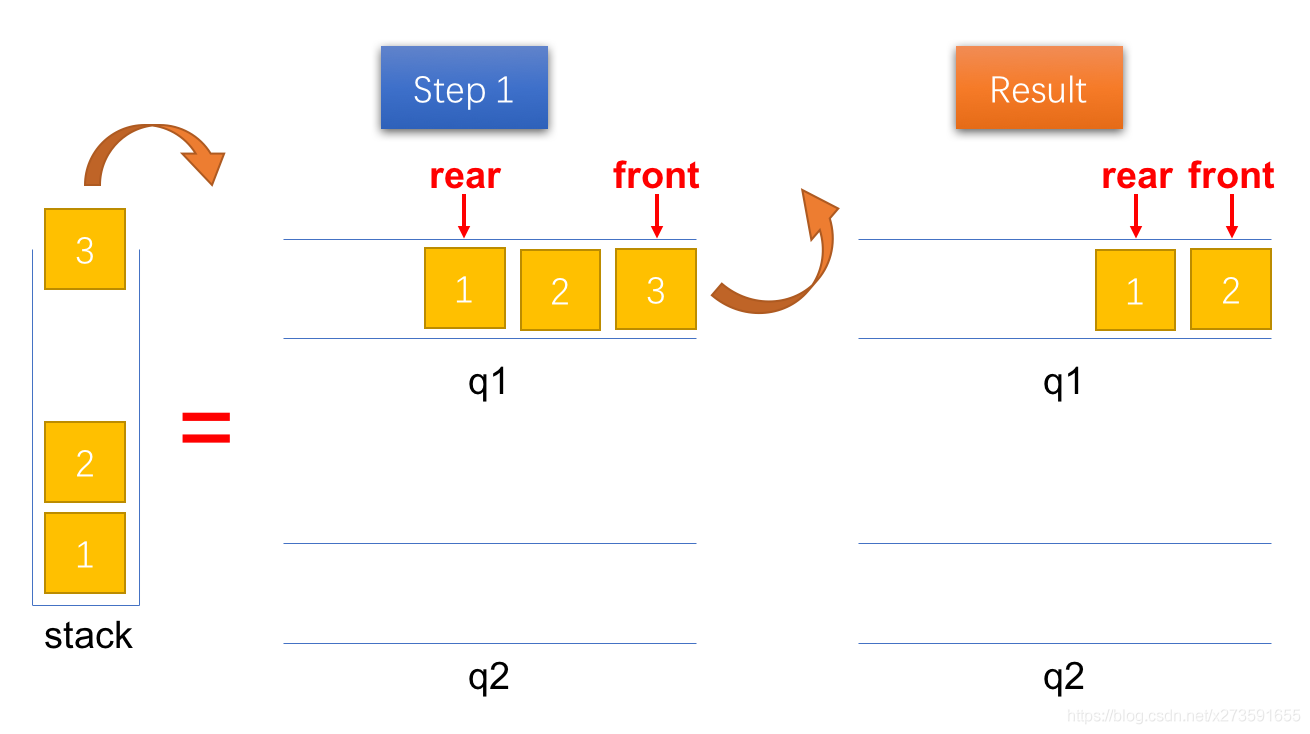
图4:将一个元素出栈
代码(Java)实现如下:
/** Removes the element on top of the stack and returns that element. */ public int pop() { if (q1.isEmpty()) { throw new NoSuchElementException("[ERROR] The stack is empty!"); } return q1.remove(); }复杂度分析如下:
时间复杂度:$ O(1) $
空间复杂度:$ O(1) $
查看栈顶元素(peek)同理,只需要返回队列1 q1 队首元素即可。
/** Get the top element. */ public int top() { if (q1.isEmpty()) { throw new NoSuchElementException("[ERROR] The stack is empty!"); } return q1.peek(); }复杂度分析如下:
时间复杂度:$ O(1) $
空间复杂度:$ O(1) $
是否为空(empty)这个操作和解法一的没什么不同,故不再赘言。
Java 实现 import java.util.LinkedList; import java.util.NoSuchElementException; import java.util.Queue; class MyStack { private Queue<Integer> q1; private Queue<Integer> q2; /** Initialize your data structure here. */ public MyStack() { q1 = new LinkedList<>(); q2 = new LinkedList<>(); } /** Push element x onto stack. */ public void push(int x) { q2.add(x); while (!q1.isEmpty()) { q2.add(q1.remove()); } Queue<Integer> temp = q1; q1 = q2; q2 = temp; } /** Removes the element on top of the stack and returns that element. */ public int pop() { if (q1.isEmpty()) { throw new NoSuchElementException("[ERROR] The stack is empty!"); } return q1.remove(); } /** Get the top element. */ public int top() { if (q1.isEmpty()) { throw new NoSuchElementException("[ERROR] The stack is empty!"); } return q1.peek(); } /** Returns whether the stack is empty. */ public boolean empty() { return q1.isEmpty(); } } Python 实现 from collections import deque class MyStack: def __init__(self): """ Initialize your data structure here. """ self._q1, self._q2 = deque(), deque() def push(self, x): """ Push element x onto stack. :type x: int :rtype: void """ self._q2.append(x) while self._q1: self._q2.append(self._q1.popleft()) self._q1, self._q2 = self._q2, self._q1 def pop(self): """ Removes the element on top of the stack and returns that element. :rtype: int """ if not self._q1: raise Exception("[ERROR] The stack is empty!") return self._q1.popleft() def top(self): """ Get the top element. :rtype: int """ if not self._q1: raise Exception("[ERROR] The stack is empty!") return self._q1[0] def empty(self): """ Returns whether the stack is empty. :rtype: bool """ return not self._q1 解法三:单队列 思路上面两种解法都借助于两个队列,实际上,只借助于一个队列也可以实现栈的先入先出效果。
入栈(push)
