更多 LeetCode 题解笔记可以访问我的 github。
@
描述使用队列实现栈的下列操作:
push(x) -- 元素 x 入栈
pop() -- 移除栈顶元素
top() -- 获取栈顶元素
empty() -- 返回栈是否为空
注意:
你只能使用队列的基本操作-- 也就是 push to back, peek/pop from front, size, 和 is empty 这些操作是合法的。
你所使用的语言也许不支持队列。 你可以使用 list 或者 deque(双端队列)来模拟一个队列 , 只要是标准的队列操作即可。
你可以假设所有操作都是有效的(例如, 对一个空的栈不会调用 pop 或者 top 操作)。
解法一:双队列,入快出慢 思路为了实现栈这种数据结构后入先出(last in first out, LIFO)的效果,解法一借助于两个队列。其中,一个队列保存栈的所有元素(设为队列1 q1),另一个队列用于辅助实现入栈、出栈的效果(设为队列2 q2)。相关操作的底层实现细节见下面对应的小节。
入栈(push)入栈时,直接将新的元素 x 压入队列1 q1 的队尾(rear),并且用变量 top 保存栈顶元素,方便后面的查看栈顶元素(peek)操作,具体的实现步骤见图1。
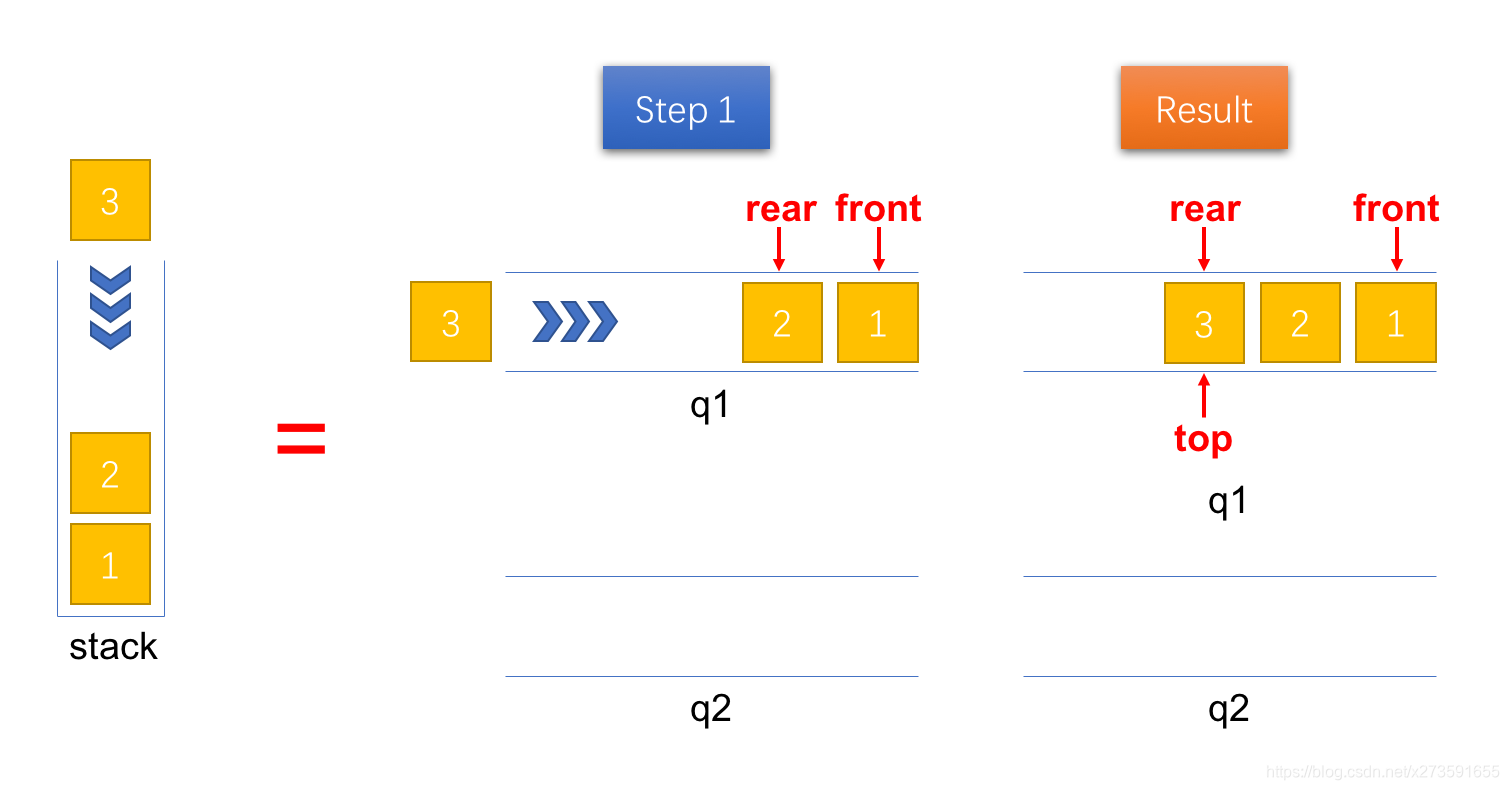
图1:将一个元素压入栈
代码(Java)实现如下:
/** Push element x onto stack. */ public void push(int x) { top = x; q1.add(x); }复杂度分析如下:
时间复杂度:$ O(1) $
空间复杂度:$ O(1) $
出栈(pop)由于入栈时直接将元素入队到队列1 q1 中,因此,栈顶的元素位于队列1 q1 的尾部。为了能将栈顶元素(队列1 q1 尾部的元素)弹出,必须先将队列1 q1 队尾之前的元素出队。这里,我们借助另一个队列(辅助队列 q2)实现这一过程——将队列1 q1 队尾之前的元素出队并入队到队列2 q2 中。 之后,将队列1 q1 中唯一个元素(栈顶元素)出队。最后,再将两个队列的引用进行交换即可完成出栈操作。具体的实现步骤如图2所示。
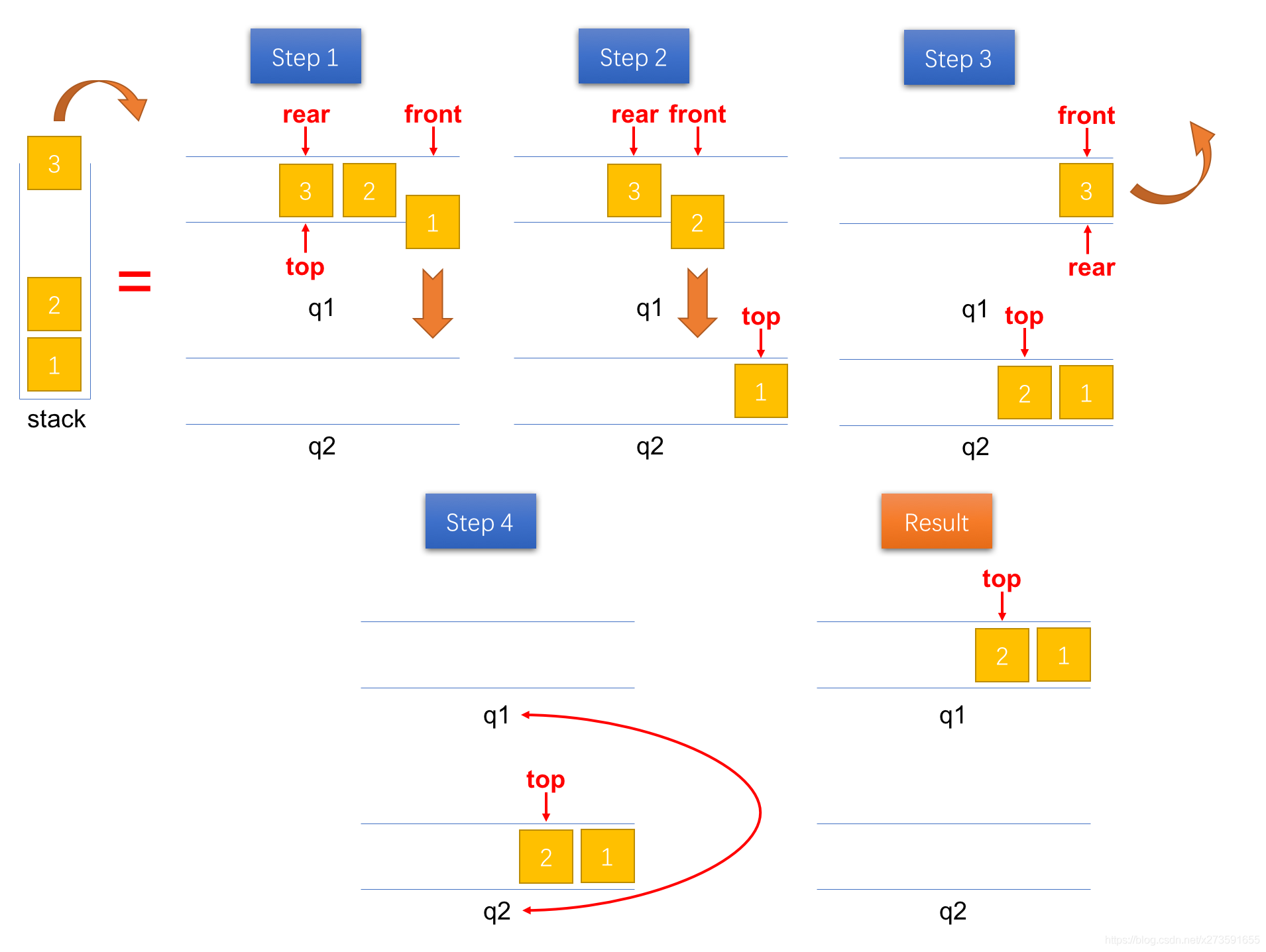
图2:将一个元素出栈
代码(Java)实现如下:
/** Removes the element on top of the stack and returns that element. */ public int pop() { if (q1.size() == 0) { throw new NoSuchElementException("[ERROR] The queue is empty!"); } while (q1.size() > 1) { top = q1.remove(); q2.add(top); } int res = q1.remove(); Queue<Integer> temp = q1; q1 = q2; q2 = temp; return res; }复杂度分析如下:
时间复杂度:$ O(n) $,其中 \(n\) 表示未出栈前元素的数目。出栈操作需要从队列1 q1 出队 \(n\) 个元素,同时入队 \(n-1\) 个元素到队列2 q2,因此需要 \(2n - 1\) 次操作。因此 LinkedList 的添加和删除操作的时间复杂度是 \(O(1)\) 的,因此,总的时间复杂度为 \(O(n)\)
空间复杂度:$ O(1) $
查看栈顶元素(peek)因为我们用变量 top 保存了栈顶的元素,因此只需要返回该变量即可,代码(Java)实现如下:
/** Get the top element. */ public int top() { return top; }复杂度分析如下:
时间复杂度:$ O(1) $
空间复杂度:$ O(1) $
是否为空(empty)队列1 q1 中保存了栈中的所有元素,因此,如果想要知道栈是否为空,只需要判断队列1 q1 中是否还有元素,代码(Java)实现如下:
/** Returns whether the stack is empty. */ public boolean empty() { return q1.isEmpty(); }复杂度分析如下:
时间复杂度:$ O(1) $
空间复杂度:$ O(1) $
Java 实现 import java.util.NoSuchElementException; import java.util.LinkedList; import java.util.Queue; class MyStack { /** * The main queue using to store all the elements in the stack */ private Queue<Integer> q1; /** * The auxiliary queue using to implement `pop` operation */ private Queue<Integer> q2; /** * The top element in the stack */ private int top; /** Initialize your data structure here. */ public MyStack() { q1 = new LinkedList<>(); q2 = new LinkedList<>(); } /** Push element x onto stack. */ public void push(int x) { top = x; q1.add(x); } /** Removes the element on top of the stack and returns that element. */ public int pop() { if (q1.size() == 0) { throw new NoSuchElementException("[ERROR] The stack is empty!"); } while (q1.size() > 1) { top = q1.remove(); q2.add(top); } int res = q1.remove(); Queue<Integer> temp = q1; q1 = q2; q2 = temp; return res; } /** Get the top element. */ public int top() { return top; } /** Returns whether the stack is empty. */ public boolean empty() { return q1.isEmpty(); } } Python 实现 from collections import deque class MyStack: def __init__(self): """ Initialize your data structure here. """ self._q1, self._q2, self._top = deque(), deque(), None def push(self, x): """ Push element x onto stack. :type x: int :rtype: void """ self._top = x self._q1.append(x) def pop(self): """ Removes the element on top of the stack and returns that element. :rtype: int """ if not self._q1: raise Exception("[ERROR] The stack is empty!") while len(self._q1) > 1: self._top = self._q1.popleft() self._q2.append(self._top) res = self._q1.popleft() self._q1, self._q2 = self._q2, self._q1 return res def top(self): """ Get the top element. :rtype: int """ return self._top def empty(self): """ Returns whether the stack is empty. :rtype: bool """ return not self._q1 解法二:双队列,入慢出快 思路
