
代码模板
public static void insertSort(int[] array){
// 第一个元素被认为默认有序,所以遍历无序元素从i1开始。
for(int i=1;i<array.length;i++){
int sortItem = array[i];
int j = i;
// 将当前元素插入到前面的有序元素里,将当前元素与前面有序元素从后往前挨个对比,然后将元素插入到指定位置。
while (j>0 && sortItem < array[j-1]){
array[j] = array[j-1];
j--;
}
// 若当前元素在前面已排序里面不是最大的,则将它插入到前面已经确定了位置里。
if(j !=i){
array[j] = sortItem;
}
}
}
插入排序总结
插入排序也是采用的内部排序,所以空间复杂度是O(1),但是时间复杂度就是O(n^2),因为基本上每个元素都要处理多次,需要反复将已排序元素移动,然后将数据插入到指定的位置。
希尔排序
希尔排序是插入排序的一个升级版,它主要是将原先的数据分成若干个子序列,然后将每个子序列进行插入排序,然后每次拆得子序列数量逐次递减,直到拆的子序列的长度等于原数据长度。然后再将数据整体来依次插入排序。
主要步骤:
选择一个增量序列 t1,t2,……,tk,其中 ti > tj, tk = 1;
按增量序列个数 k,对序列进行 k 趟排序;
每趟排序,根据对应的增量 ti,将待排序列分割成若干长度为 m 的子序列,分别对各子表进行直接插入排序。仅增量因子为 1 时,整个序列作为一个表来处理,表长度即为整个序列的长度。
过程演示
原始未排序的数据。

经过初始增量gap=array.length/2=5分组后,将原数据分为了5组,[12,1]、[29,30]、[5,45]、[16,26]、[15,32]。
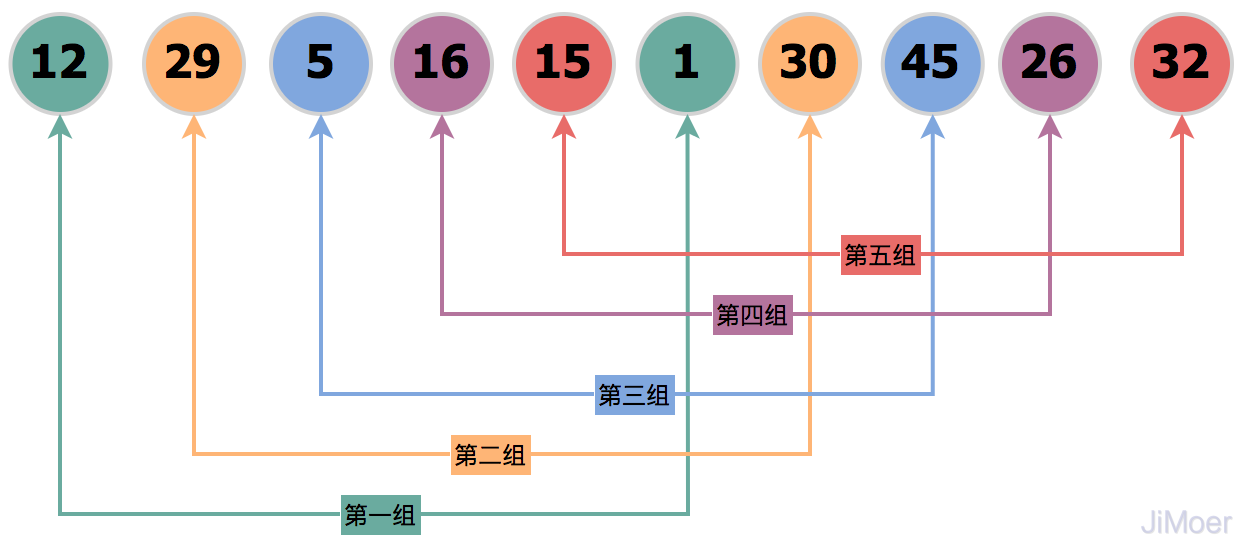
将分组后的数据,每一组数据都直接执行插入排序,这样数据已经慢慢有序起来了,然后再缩小增量gap=5/2=2,将数据分为2组:[1,5,15,30,26]、[29,16,12,45,32]。
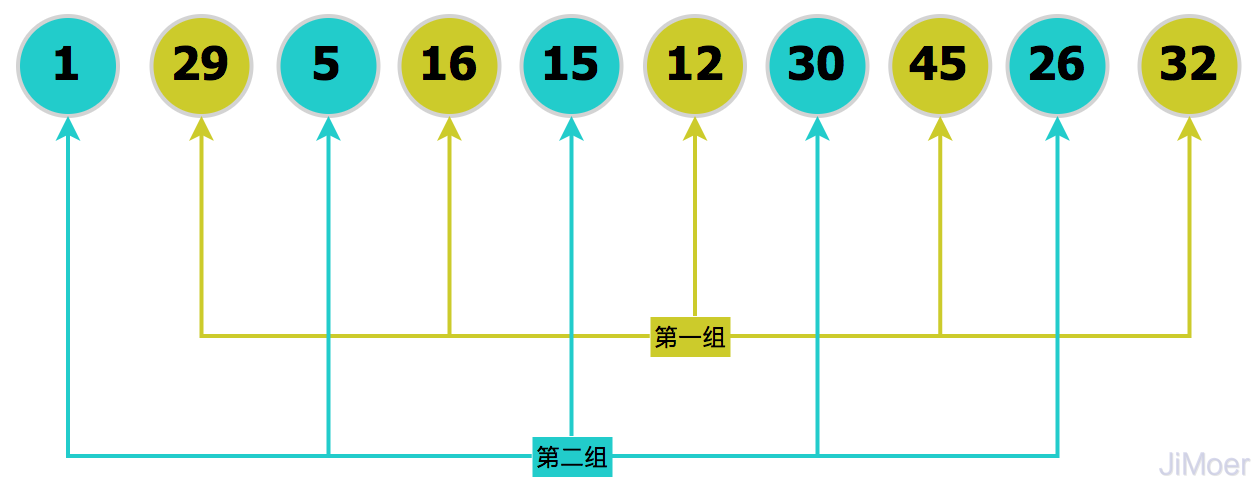
对上面已经分好的两组进行插入排序,整个数据就更加趋向有序了,然后再缩小增量gap=2/2=1,整个数据成为了1组,整个序列作为了表来处理,然后再执行一次插入排序,数据最终达到了有序。
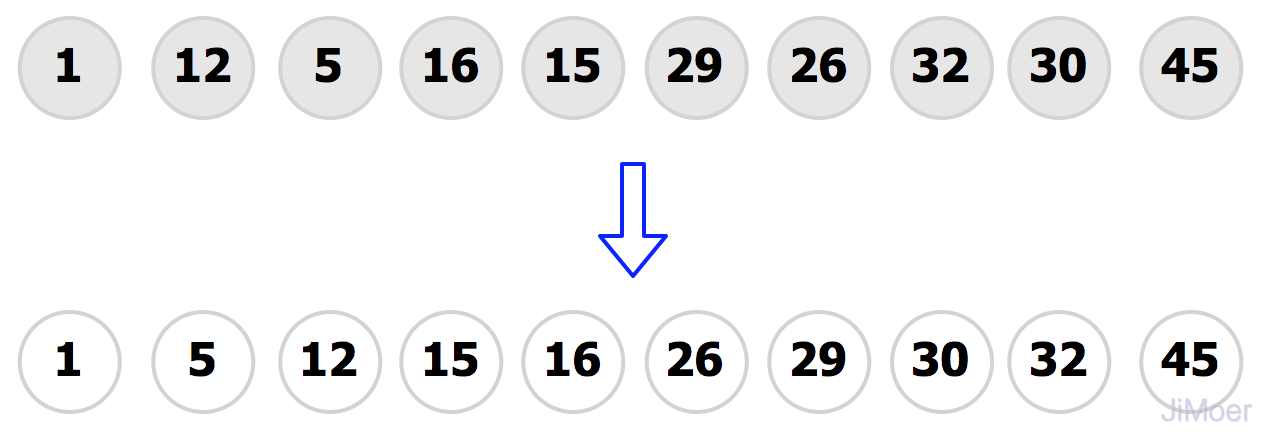
代码模板
/**
* 希尔排序
* @param array
*/
public static void shellSort(int[] array){
int len = array.length;
int temp, gap = len / 2;
while (gap > 0) {
for (int i = gap; i < len; i++) {
temp = array[i];
int preIndex = i - gap;
while (preIndex >= 0 && array[preIndex] > temp) {
array[preIndex + gap] = array[preIndex];
preIndex -= gap;
}
array[preIndex + gap] = temp;
}
gap /= 2;
}
}
归并排序
归并排序是采用的分而治之的递归方式来完成数据排序的,主要是将已有序的两个子序列,合并成一个新的有序子序列。先将子序列分段有序,然后再将分段后的子序列合并成,最终完成数据的排序。
主要步骤:
将数据的长度从中间一分为二,分成两个子序列,执行递归操作,直到每个子序列就剩两个元素。
然后分别对这些拆好的子序列进行归并排序。
将排序好的子序列再两两合并,最终合并成一个完整的排序序列。
动图演示

代码模板
/**
* 归并排序
* @param array
数组
* @param left
0
* @param right
array.length-1
*/
public static void mergeSort(int[] array,int left,int right){
if (right <= left){
return;
}
// 一分为二
int mid = (left + right)/2;
// 对前半部分执行归并排序
mergeSort(array, left, mid);
// 对后半部分执行归并排序
mergeSort(array, mid + 1, right);
// 将分好的每个子序列,执行排序加合并操作
merge(array, left, mid, right);
}
/**
* 合并加排序
* @param array
* @param left
* @param middle
* @param right
*/
public static void merge(int[] array,int left,int middle,int right){
// 中间数组
int[] temp = new int[right - left + 1];
int i = left, j = middle + 1, k = 0;
while (i <= middle && j <= right) {
// 若前面数组的元素小,就将前面元素的数据放到中间数组中
if(array[i] <= array[j]){
temp[k++] = array[i++];
}else {
// 若后面数组的元素小,就将后面数组的元素放到中间数组中
temp[k++] = array[j++];
}
}
// 若经过上面的比较合并后,前半部分的数组还有数据,则直接插入中间数组后面
while (i <= middle){
temp[k++] = array[i++];
}
// 若经过上面的比较合并后,后半部分的数组还有数据,则直接插入中间数组后面
while (j <= right){
temp[k++] = array[j++];
}
// 将数据从中间数组中复制回原数组
for (int p = 0; p < temp.length; p++) {
array[left + p] = temp[p];
}
}
归并排序总结







