Java实现十个经典排序算法（带动态效果图）

排序算法是老生常谈的了，但是在面试中也有会被问到，例如有时候，在考察算法能力的时候，不让你写算法，就让你描述一下，某个排序算法的思想以及时间复杂度或空间复杂度。我就遇到过，直接问快排的，所以这次我就总结梳理一下经典的十大排序算法以及它们的模板代码。

算法分析

一个排序算法的好坏，一般是通过下面几个关键信息来分析的，下面先介绍一下这几个关键信息，然后再将常见的排序算法的这些关键信息统计出来。

名词介绍

时间复杂度：指对数据操作的次数（或是简单的理解为某段代码的执行次数）。举例：O(1)：常数时间复杂度；O(log n)：对数时间复杂度；O(n)：线性时间复杂度。

空间复杂度：某段代码每次执行时需要开辟的内存大小。

内部排序：不依赖外部的空间，直接在数据内部进行排序；

外部排序：数据的排序，不能通过内部空间来完成，需要依赖外部空间。

稳定排序：若两个元素相等：a=b，排序前a排在b前面，排序后a仍然在b后面，称为稳定排序。

不稳定排序：若两个元素相等：a=b，排序前a排在b前面，排序后a有可能出现在b后面，称为不稳定排序。

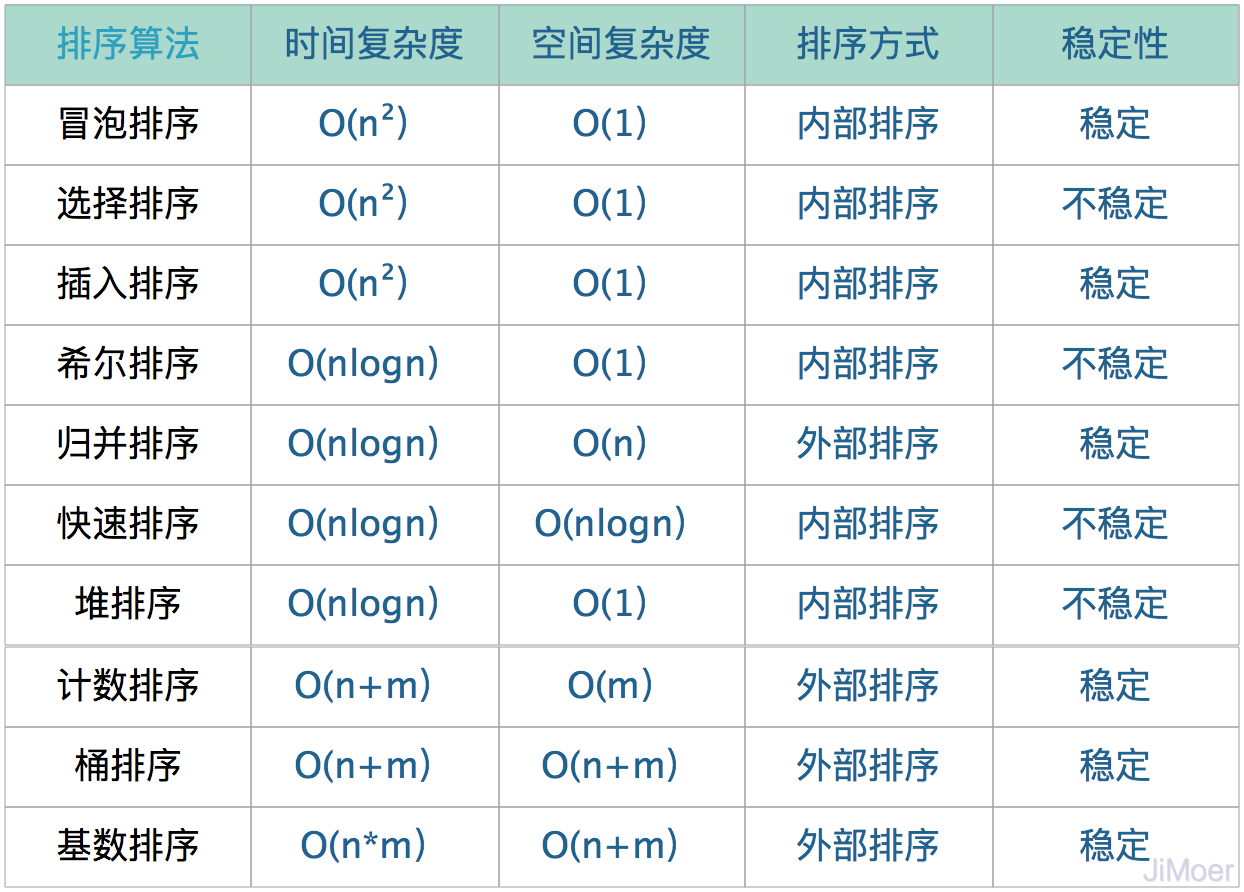
常见的排序算法的这几个关键信息如下：

冒泡排序

冒泡排序是一种简单直观的排序算法，它需要多次遍历数据；
主要有这么几步：

将相邻的两个元素进行比较，如果前一个元素比后一个元素大那么就交换两个元素的位置，经过这样一次遍历后，最后一个元素就是最大的元素了；

然后再将除最后一个元素的剩下的元素，重复执行上面相邻两元素比较的步骤。

每次对越来越少的元素重复上面的步骤，直到就剩一个数字需要比较。

这样最终达到整体数据的一个有序性了。

动图演示

代码模板 /** * 冒泡排序 * @param array */ public static void bubbleSort(int[] array){ if(array.length == 0){ return; } for(int i=0;i<array.length;i++){ // 每一次都减少i个元素 for(int j=0;j<array.length-1-i;j++){ // 若相邻的两个元素比较后，前一个元素大于后一个元素，则交换位置。 if(array[j]>array[j+1]){ int temp = array[j]; array[j] = array[j+1]; array[j+1] = temp; } } } } 冒泡排序总结

当数组中的元素已经是正序时，执行效率最高。
当数组中的元素是一个倒序时，执行效率最低，相邻的元素每次比较都需要交换位置。
而且冒泡排序是完全在数据内部进行的，不需要额外的空间，所以空间复杂度是O(1)。

选择排序

选择排序是一种简单粗暴的排序方式，每次都从数据中选出最大或最小的元素，最终选完了，那么选出来的数据就是排好序的了。

主要步骤：

先从全部数据中选出最小的元素，放到第一个元素的位置（选出最小元素和第一位位置交换位置）；

然后再从除了第一个元素的剩余元素中再选出最小的元素，然后放到数组的第二个位置上。

循环重复上面的步骤，最终选出来的数据都放前面了，数据就排好序了。

动图演示

代码模板 public static void selectSort(int[] array){ for(int i=0;i<array.length;i++){ // 先以i为最小值的下标 int min = i; // 然后从后面的数据中找出比array[min] 还小的值，就替换min为当前下标。 for(int j=i+1;j<array.length;j++){ if(array[j]<array[min]){ min = j; } } // 最终如果最小值的下标不等于i了，那么将最小值与i位置的数据替换，即将最小值放到数组前面来，然后循环整个操作。 if(min != i){ int temp = array[i]; array[i] = array[min]; array[min] = temp; } } } 选择排序总结

所有的数据经过选择排序，时间复杂度都是O(n^2)；所以需要排序的数据量越小选择排序的效率越高。

插入排序

插入排序也是一种比较直观和容易理解的排序算法，通过构建有序序列，将未排序中的数据插入到已排序中序列，最终未排序全部插入到有序序列，达到排序效果。

主要步骤：

将原始数据的第一个元素当成已排序序列，然后将除了第一个元素的后面元素当成未排序序列。

从后面未排序元素中从前到后扫描，挨个取出元素，在已排序的序列中从后往前扫描，将从未排序序列中取出的元素插入到已排序序列的指定位置。

当未排序元素数量为0时，则排序完成。

动图演示