缺点就是需要对堆进行多次搜索,毕竟是在一个空间内又标记,又移动的,所以整体而言花费的时间较多,而且如果堆很大的情况,那么消耗的时间将更加突出。
至此相信你对标记-清除、标记-复制和标记-整理都清晰了,让我们再回到刚才提到的分代收集。
跨代引用我们已经根据对象存活的特性进行了分代,提高了垃圾收集的效率,但是像在回收新生代的时候,有可能有老年代的对象引用了新生代对象,所以老年代也需要作为根,但是如果扫描整个老年代的话效率就又降低了。
所以就搞了个叫记忆集(Remembered Set)的东西,来记录跨代之间的引用而避免扫描整体非收集区域。
因此记忆集就是一种用于记录从非收集区域指向收集区域的指针集合的抽象数据结构。根据记录的精度分为
字长精度,每条记录精确到机器字长。
对象精度,每条记录精确到对象。
卡精度,每条记录精确到一块内存区域。
最常见的是用卡精度来实现记忆集,称之为卡表。
我来解释下什么叫卡。
拿对象精度来距离,假设新生代对象 A 被老年代对象 D 引用了,那么就需要记录老年代 D 所在的地址引用了新生代对象。
那卡的意思就是将内存空间分成很多卡片。假设新生代对象 A 被老年代 D 引用了,那么就需要记录老年代 D 所在的那一块内存片有引用新生代对象。
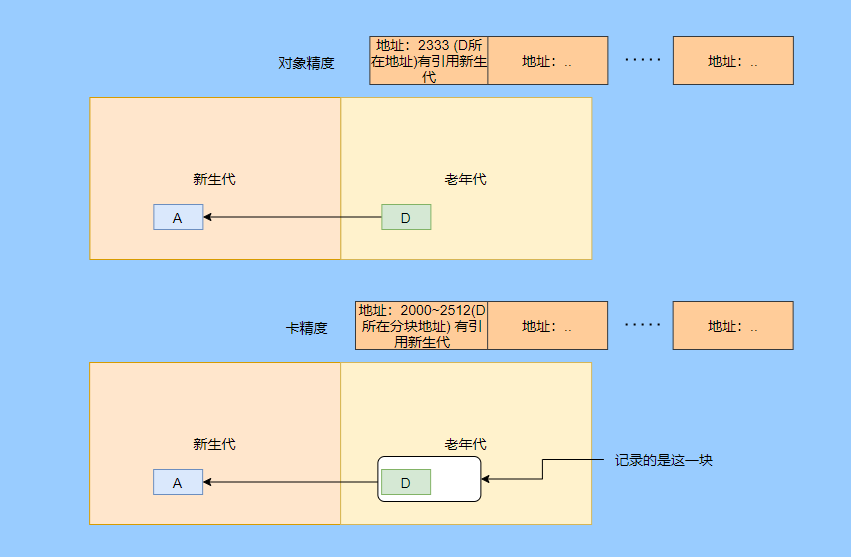
也就是说堆被卡切割了,假设卡的大小是 2,堆是 20,那么堆一共可以划分成 10 个卡。
因为卡的范围大,如果此时 D 旁边在同一个卡内的对象也有引用新生代对象的话,那么就只需要一条记录。
一般会用字节数组来实现卡表,卡的范围也是设为 2 的 N 次幂大小。来看一下图就很清晰了。

假设地址从 0x0000 开始,那么字节数组的 0号元素代表 0x0000~0x01FF,1 号代表0x0200~0x03FF,依次类推即可。
然后到时候回收新生代的时候,只需要扫描卡表,把标识为 1 的脏表所在内存块加入到 GC Roots 中扫描,这样就不需要扫描整个老年代了。
用了卡表的话占用内存比较少,但是相对字长、对象来说精度不准,需要扫描一片。所以也是一种取舍,到底要多大的卡。
还有一种多卡表,简单的说就是有多张卡表,这里我画两张卡表示意一下。

上面的卡表表示的地址范围更大,这样可以先扫描范围大的表,发现中间一块脏了,然后再通过下标计算直接得到更具体的地址范围。
这种多卡表在堆内存比较大,且跨代引用较少的时候,扫描效率较高。
而卡表一般都是通过写屏障来维护的,写屏障其实就相当于一个 AOP,在对象引用字段赋值的时候加入更新卡表的代码。
这其实很好理解,说白了就是当引用字段赋值的时候判断下当前对象是老年代对象,所引用对象是新生代对象,于是就在老年代对象所对应的卡表位置置为 1,表示脏,待会需要加入根扫描。
不过这种将老年代作为根来扫描会有浮动垃圾的情况,因为老年代的对象可能已经成为垃圾,所以拿垃圾来作为根扫描出来的新生代对象也很有可能是垃圾。
不过这是分代收集必须做出的牺牲。
增量式 GC所谓的增量式 GC 其实就是在应用线程执行中,穿插着一点一点的完成 GC,来看个图就很清晰了
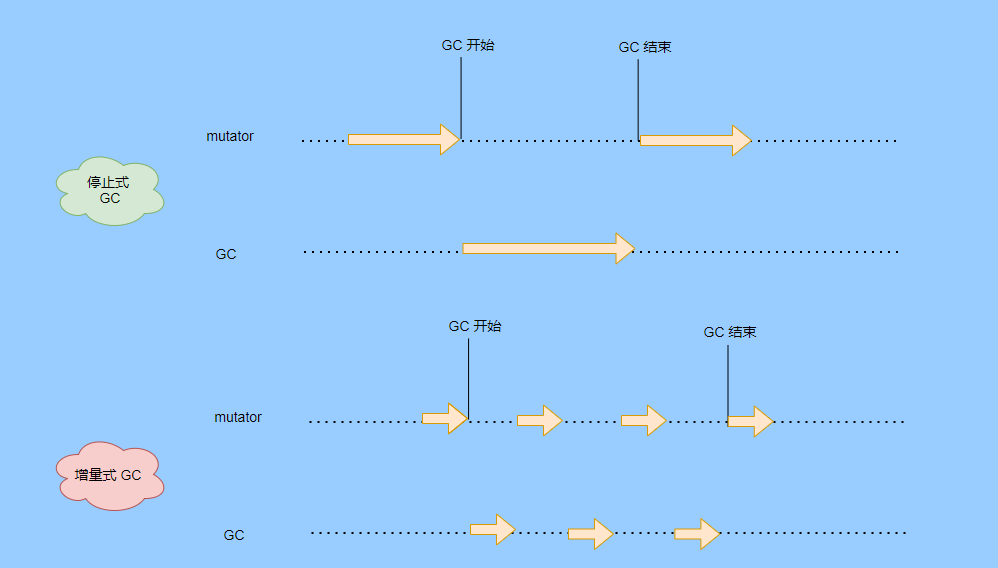
这样看起来 GC 的时间跨度变大了,但是 mutator 暂停的时间变短了。
对于增量式 GC ,Dijkstra 等人抽象除了三色标记算法,来表示 GC 中对象三种不同状况。
三色标记算法白色:表示还未搜索到的对象。
灰色:表示正在搜索还未搜索完的对象。
黑色:表示搜索完成的对象。
下面这图从维基百科搞得,虽说颜色没对上,但是意思是对的(black 画成了蓝色,grey画成了黄色)。

我再用文字概述一下三色的转换。
GC 开始前所有对象都是白色,GC 一开始所有根能够直达的对象被压到栈中,待搜索,此时颜色是灰色。
然后灰色对象依次从栈中取出搜索子对象,子对象也会被涂为灰色,入栈。当其所有的子对象都涂为灰色之后该对象被涂为黑色。
当 GC 结束之后灰色对象将全部没了,剩下黑色的为存活对象,白色的为垃圾。
一般增量式标记-清除会分为三个阶段:
根查找,需要暂停应用线程,找到根直接引用的对象。
标记阶段,和应用线程并发执行。
清除阶段。
这里解释下 GC 中两个名词的含义。
并发:应用线程和 GC 线程一起执行。
并行:多个 GC 线程一起执行。
看起来好像三色标记没啥问题?来看看下图。
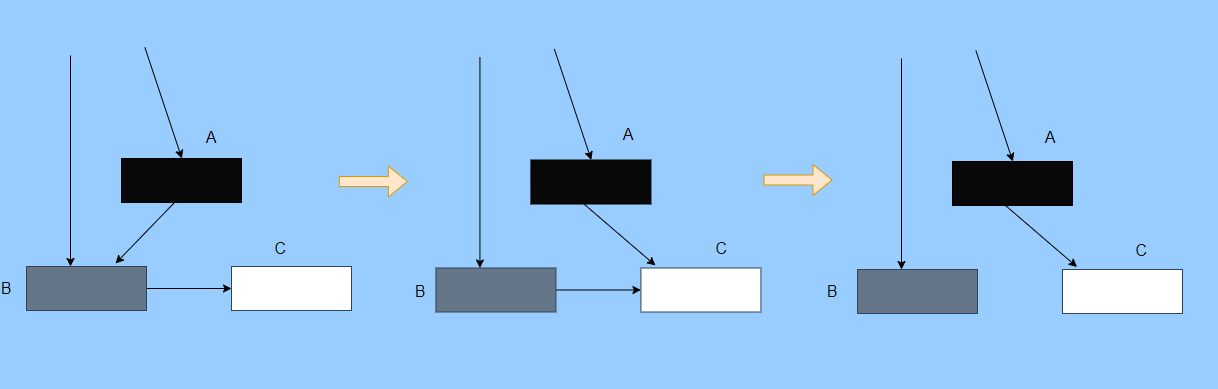
第一个阶段搜索到 A 的子对象 B了,因此 A 被染成了黑色,B 为灰色。此时需要搜索 B。
但是在 B 开始搜索时,A 的引用被 mutator 换给了 C,然后此时 B 到 C 的引用也被删了。
接着开始搜索 B ,此时 B 没有引用因此搜索结束,这时候 C 就被当垃圾了,因此 A 已经黑色了,所以不会再搜索到 C 了。
这就是出现漏标的情况,把还在使用的对象当成垃圾清除了,非常严重,这是 GC 不允许的,宁愿放过,不能杀错。

