这是《冷饭新炒》系列的第六篇文章。

本文会翻炒一个用途比较广的算法 - 布隆过滤器算法。
布隆过滤器的一些概念主要包括:
简介
算法
参数
优势和劣势
布隆过滤器简介布隆过滤器是一种空间高效概率性的数据结构(百科中原文是a space-efficient probabilistic data structure),该数据结构于1970年由Burton Howard Bloom提出,作用是测试一个元素是否某个集合的一个成员。布隆过滤器是可能出现false positive(这个是专有名词"假阳性",可以理解为误判的情况,下文如果用到这个名词会保留英文单词使用)匹配的,换言之,布隆过滤器在使用的时候有可能返回结果"可能存在于集合中"或者"必定不存在于集合中"。
布隆过滤器算法描述在场景复杂的网络爬虫中,爬取到的网页URL依赖有可能成环,例如在URL-1页面中展示了URL-2,然后又在URL-2中的页面展示了URL-1,这个时候需要一种方案记录和判断历史访问过的URL。这个时候可能会想到下面的方案:
方案一:使用数据库存储已经访问过的URL,例如MySQL表中基于URL建立唯一索引或者使用Redis的SET数据类型
方案二:使用HashSet(其实这里不局限于HashSet,链表、树和散列表等数据结构都能满足)存储已经访问过的URL
方案三:基于方案一和方案二进行优化,存储URL的摘要,使用摘要算法如MD5、SHA-n算法针对URL字符串生成摘要
方案四:使用Hash函数处理对应的URL生成一个哈希码,再把哈希码通过一个映射函数映射到一个固定容量的BitSet中的某一个比特
对于方案一、方案二和方案三,在历史访问URL数据量极大的情况下,会消耗巨大的存储空间(磁盘或者内存),对于方案四,如果URL有100亿个,那么要把冲突几率降低到1%,那么BitSet的容量需要设置为10000亿。
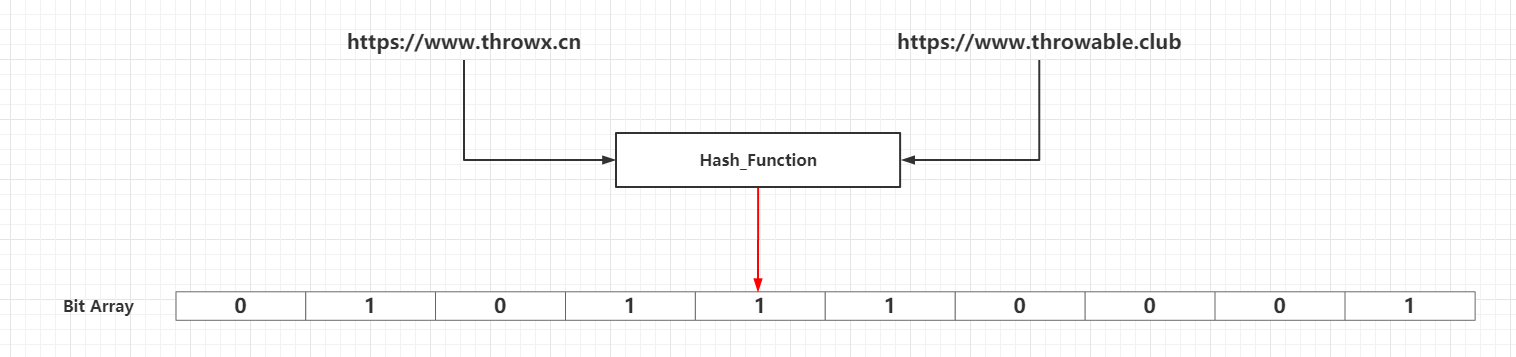
所以上面的四种方案都有明显的不足之处,而布隆过滤器算法的基本思路跟方案四差不多,最大的不同点就是方案四中只提到使用了一个散列函数,而布隆过滤器中使用了k(k >= 1)个相互独立的高效低冲突的散列函数。
一个初始化的布隆过滤器是一个所有比特都设置为0的长度为m的比特数组,也就是认知中的Bit Array、Bit Set或者Redis中的Bit Map概念。然后需要引入k个不同的散列函数,某个新增元素通过这k个散列函数处理之后,映射到比特数组m个比特中的k个,并且把这些命中映射的k个比特位设置为1,产生一个均匀的随机分布。通常情况下,k的一个较小的常数,取决于所需的误判率,而布隆过滤器容量m与散列函数个数k和需要添加元素数量呈正相关。
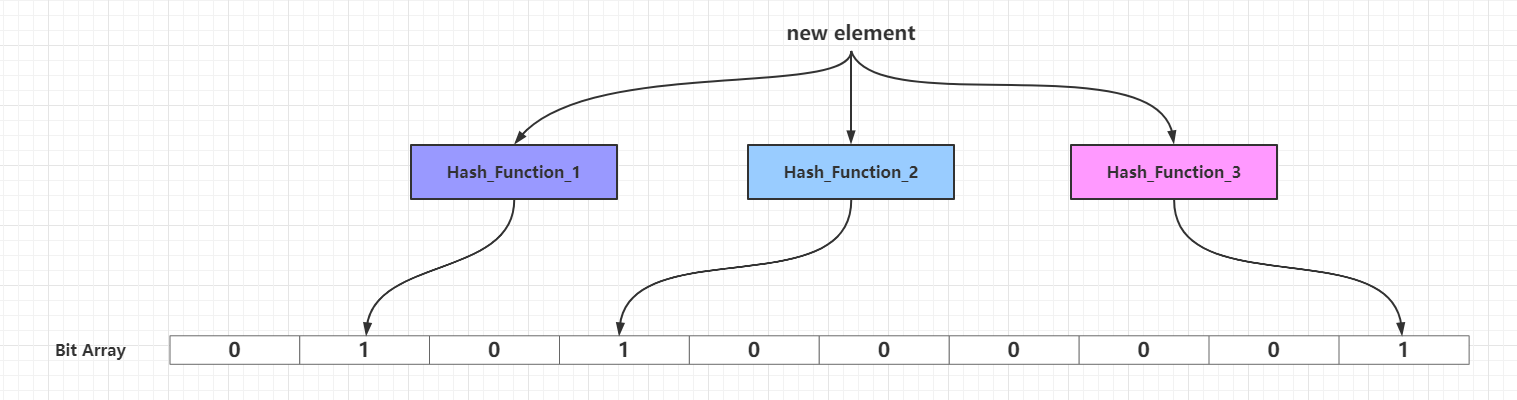
当需要新增的所有元素都添加到布隆过滤器之后,那么比特数组中的很多比特都被设置为1。这个时候如果需要判断一个元素是否存在于布隆过滤器中,只需要通过k个散列函数处理得到比特数组的k个下标,然后判断比特数组对应的下标所在比特是否为1。如果这k个下标所在比特中至少存在一个0,那么这个需要判断的元素必定不在布隆过滤器代表的集合中;如果这k个下标所在比特全部都为1,那么那么这个需要判断的元素可能存在于布隆过滤器代表的集合中或者刚好是一个False Positive,至于误差率分析见下文的布隆过滤器的相关参数一节。False Positive出现的情况可以见下图:
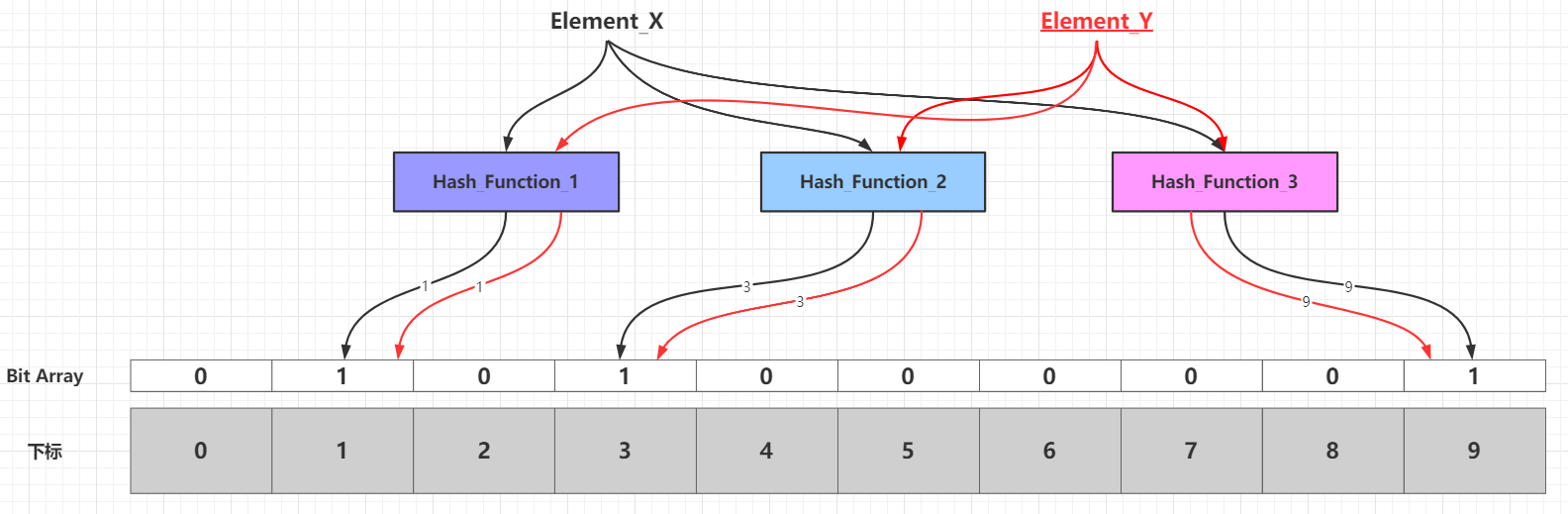
当添加到布隆过滤器的元素数量比较大,并且布隆过滤器的容量设置不合理(过小),容易出现多个元素通过k个散列函数,映射到相同的k个位(如上图的下标1、3、9所在的位),这个时候就无法准确判断这k个位由具体那个元素映射而来。其实可以极端一点思考:假设布隆过滤器容量为24,散列函数只有一个,那么添加最多25个不同元素,必定有两个不同的元素的映射结果落在同一个位。
布隆过滤器的相关参数在算法描述一节已经提到过,布隆过滤器主要有下面的参数:
初始化比特数组容量m
散列函数个数k
误判率ε(数学符号Epsilon,代表False Positive Rate)
需要添加到布隆过滤器的元素数量n
考虑到篇幅原因,这里不做这几个值的关系推导,直接整理出结果和关系式。
误判率ε的估算值为:[1 - e^(-kn/m)]^k
最优散列函数数量k的推算值:对于给定的m和n,当k = m/n * ln2的时候,误判率ε最低
推算初始化比特容量m的值,当k = m/n * ln2的时候,m >= n * log2(e) * log2(1/ε)
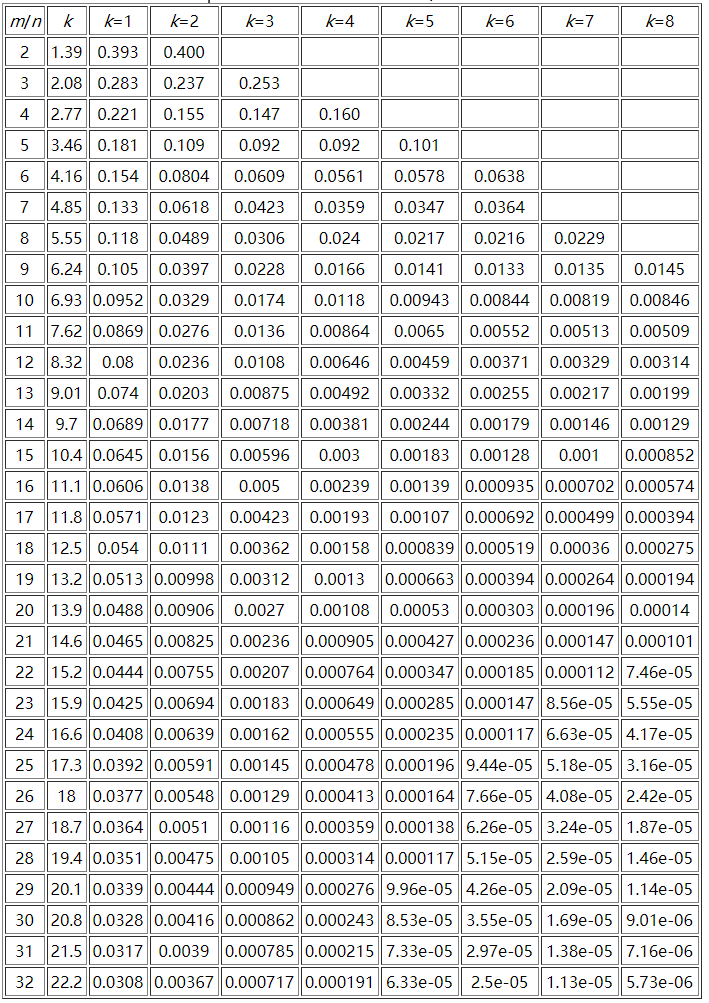
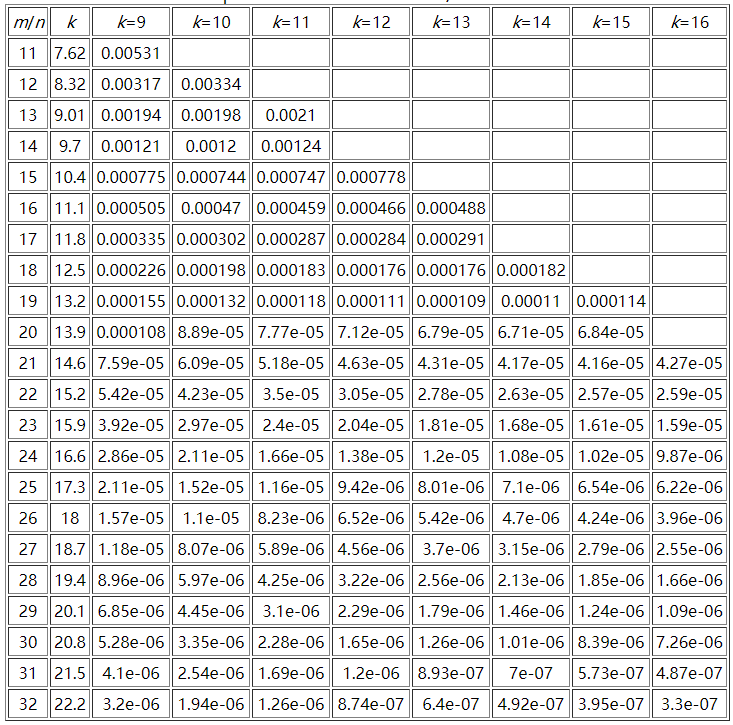
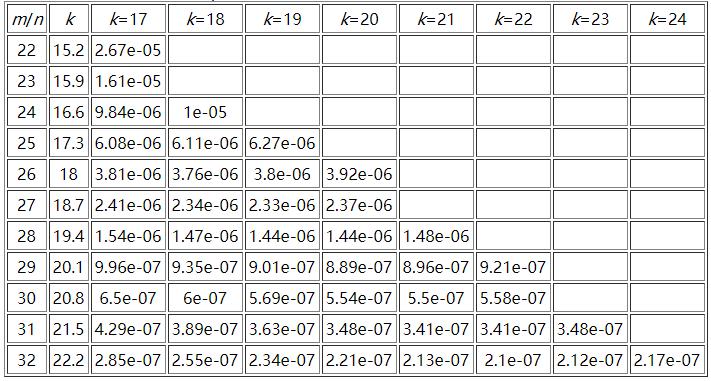
这里贴一个参考资料中m/n、k和False Positive Rate之间的关系图: