布隆过滤器的变体十分多,主要是为了解决布隆过滤器算法中的一些缺陷或者劣势。常见的变体如下:
变体名称 变体描述Counting Bloom Filter 把原生布隆过滤器每个位替换成一个小的计数器(Counter),所谓计数器其实就是一个小的整数
Compressed Bloom Filter 对位数组进行压缩
Hierarchical Bloom Filters 分层,由多层布隆过滤器组成
Spectral Bloom Filters CBF的扩展,提供查询集合元素的出现频率功能
Bloomier Filters 存储函数值,不仅仅是做位映射
Time-Decaying Bloom Filters 计数器数组替换位向量,优化每个计数器存储其值所需的最小空间
Space Code Bloom Filter -
Filter Banks -
Scalable Bloom filters -
Split Bloom Filters -
Retouched Bloom filters -
Generalized Bloom Filters -
Distance-sensitive Bloom filters -
Data Popularity Conscious Bloom Filters -
Memory-optimized Bloom Filter -
Weighted Bloom filter -
Secure Bloom filters -
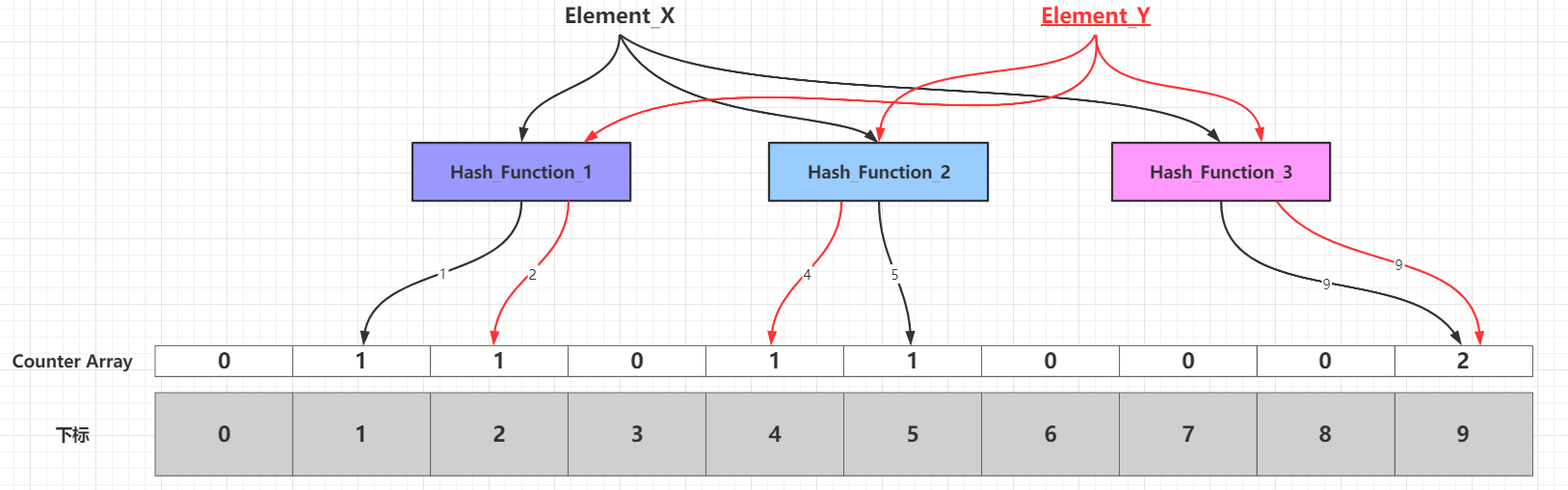
这里挑选Counting Bloom Filter(简称CBF)变体稍微展开一下。原生布隆过滤器的基础数据结构是位向量,CBF扩展原生布隆过滤器的基础数据结构,底层数组的每个元素使用4位大小的计数器存储添加元素到数组某个下标时候映射成功的频次,在插入新元素的时候,通过k个散列函数映射到k个具体计数器,这些命中的计数器值增加1;删除元素的时候,通过k个散列函数映射到k个具体计数器,这些计数器值减少1。使用CBF判断元素是否在集合中的时候:
某个元素通过k个散列函数映射到k个具体计数器,所有计数器的值都为0,那么元素必定不在集合中
某个元素通过k个散列函数映射到k个具体计数器,至少有1个计数器的值大于0,那么元素可能在集合中
一句话简单概括布隆过滤器的基本功能:不存在则必不存在,存在则不一定存在。
在使用布隆过滤器判断一个元素是否属于某个集合时,会有一定的误判率。也就是有可能把不属于某个集合的元素误判为属于这个集合,这种错误称为False Positive,但不会把属于某个集合的元素误判为不属于这个集合(相对于False Positive,"假阳性",如果属于某个集合的元素误判为不属于这个集合的情况称为False Negative,"假阴性")。False Positive,也就是错误率或者误判率这个因素的引入,是布隆过滤器在设计上权衡空间效率的关键。

