JAVA
// Global variable that records the length of an array; static int heapLen; /** * Swap the two elements of an array * @param arr * @param i * @param j */ private static void swap(int[] arr, int i, int j) { int tmp = arr[i]; arr[i] = arr[j]; arr[j] = tmp; } /** * Build Max Heap * @param arr */ private static void buildMaxHeap(int[] arr) { for (int i = arr.length / 2 - 1; i >= 0; i--) { heapify(arr, i); } } /** * Adjust it to the maximum heap * @param arr * @param i */ private static void heapify(int[] arr, int i) { int left = 2 * i + 1; int right = 2 * i + 2; int largest = i; if (right < heapLen && arr[right] > arr[largest]) { largest = right; } if (left < heapLen && arr[left] > arr[largest]) { largest = left; } if (largest != i) { swap(arr, largest, i); heapify(arr, largest); } } /** * Heap Sort * @param arr * @return */ public static int[] HeapSort(int[] arr) { // index at the end of the heap heapLen = arr.length; // build MaxHeap buildMaxHeap(arr); for (int i = arr.length - 1; i > 0; i--) { // Move the top of the heap to the tail of the heap in turn swap(arr, 0, i); heapLen -= 1; heapify(arr, 0); } return arr; }Python
def HeapSort(arr): global heapLen # 用于标记堆尾部的索引 heapLen = len(arr) # 构建最大堆 buildMaxHeap(arr) for i in range(len(arr)-1, 0, -1): # 依次将堆顶移至堆尾 swap(arr, 0, i) heapLen -= 1 heapify(arr, 0) return arr def buildMaxHeap(arr): for i in range(len(arr)//2-1, -1, -1): heapify(arr, i) def heapify(arr, i): left = 2*i + 1 right = 2*i + 2 largest = i if right < heapLen and arr[right] > arr[largest]: largest = right if left < heapLen and arr[left] > arr[largest]: largest = left if largest != i: swap(arr, largest, i) heapify(arr, largest) def swap(arr, i, j): arr[i], arr[j] = arr[j], arr[i] 算法分析稳定性:不稳定
时间复杂度:最佳:O(nlogn) 最差:O(nlogn) 平均:O(nlogn)
空间复杂度:O(1)
计数排序(Counting Sort)计数排序的核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。 作为一种线性时间复杂度的排序,计数排序要求输入的数据必须是有确定范围的整数。
计数排序(Counting sort)是一种稳定的排序算法。计数排序使用一个额外的数组C,其中第i个元素是待排序数组A中值等于i的元素的个数。然后根据数组C来将A中的元素排到正确的位置。它只能对整数进行排序。
算法步骤找出数组中的最大值max、最小值min;
创建一个新数组C,其长度是max-min+1,其元素默认值都为0;
遍历原数组A中的元素A[i],以A[i]-min作为C数组的索引,以A[i]的值在A中元素出现次数作为C[A[i]-min]的值;
对C数组变形,新元素的值是该元素与前一个元素值的和,即当i>1时C[i] = C[i] + C[i-1];
创建结果数组R,长度和原始数组一样。
从后向前遍历原始数组A中的元素A[i],使用A[i]减去最小值min作为索引,在计数数组C中找到对应的值C[A[i]-min],C[A[i]-min]-1就是A[i]在结果数组R中的位置,做完上述这些操作,将count[A[i]-min]减小1。
图解算法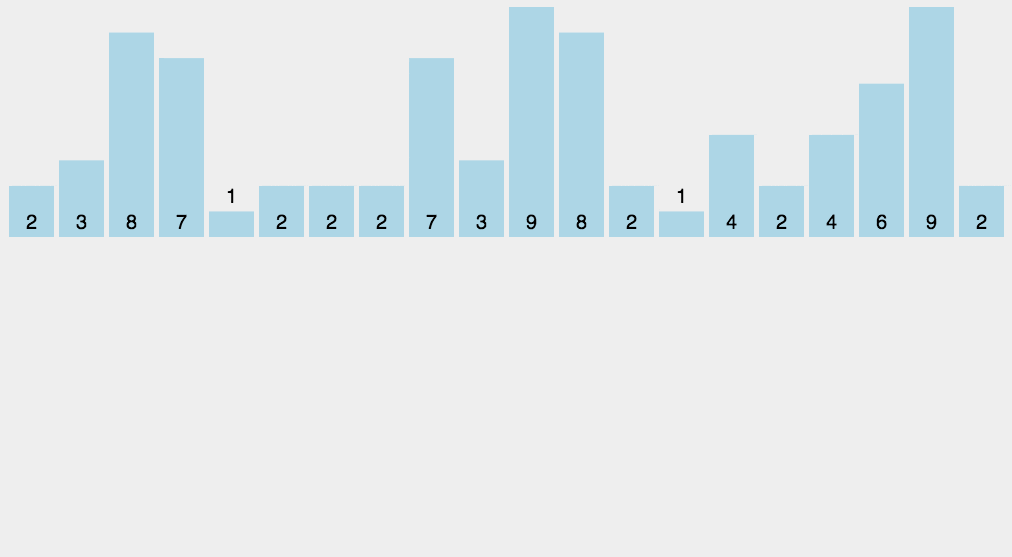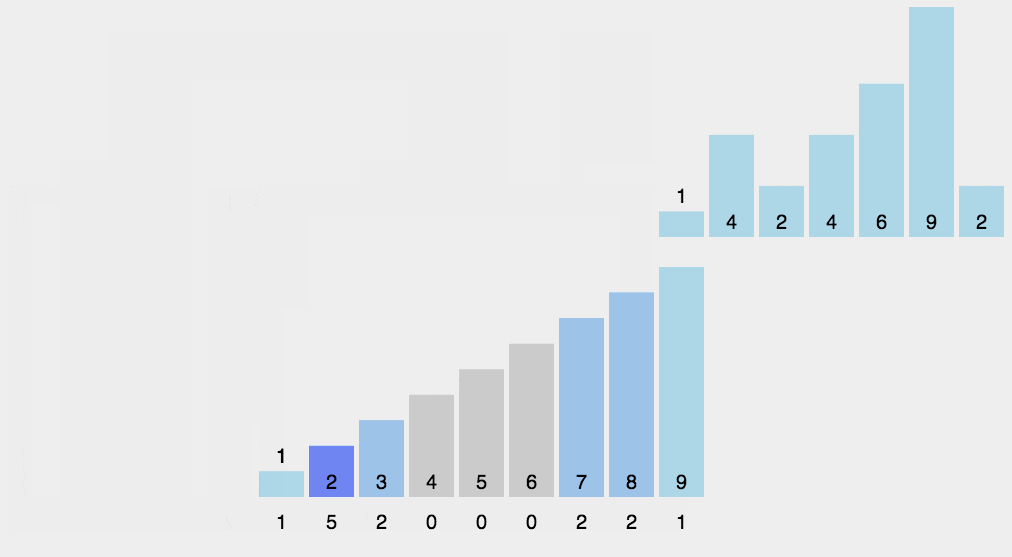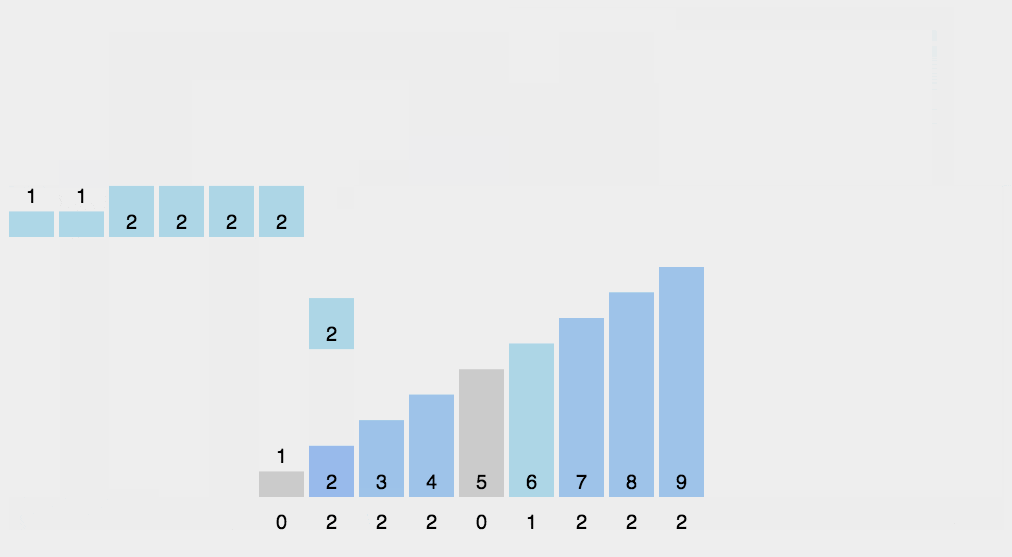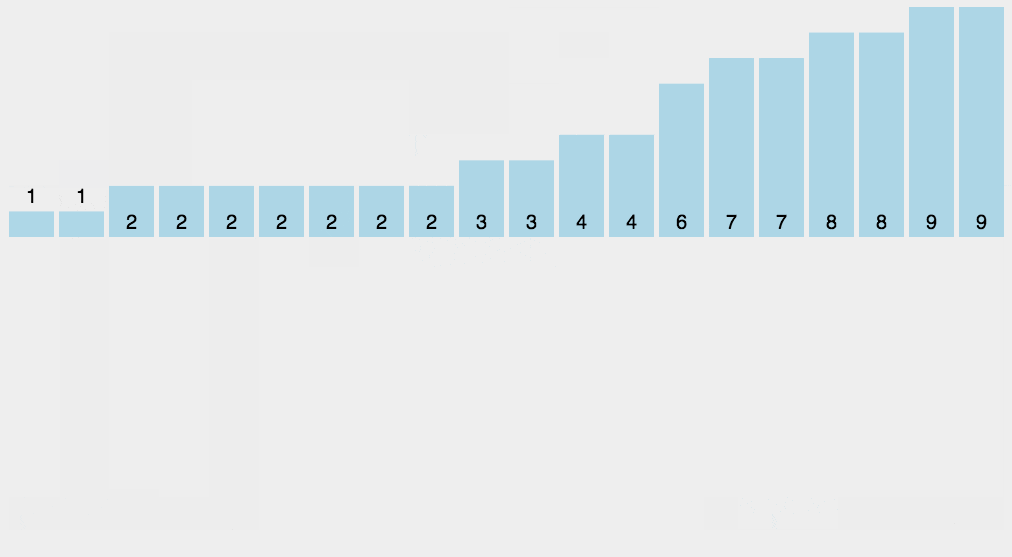
JAVA
/** * Gets the maximum and minimum values in the array * * @param arr * @return */ private static int[] getMinAndMax(int[] arr) { int maxValue = arr[0]; int minValue = arr[0]; for (int i = 0; i < arr.length; i++) { if (arr[i] > maxValue) { maxValue = arr[i]; } else if (arr[i] < minValue) { minValue = arr[i]; } } return new int[] { minValue, maxValue }; } /** * Counting Sort * * @param arr * @return */ public static int[] CountingSort(int[] arr) { if (arr.length < 2) { return arr; } int[] extremum = getMinAndMax(arr); int minValue = extremum[0]; int maxValue = extremum[1]; int[] countArr = new int[maxValue - minValue + 1]; int[] result = new int[arr.length]; for (int i = 0; i < arr.length; i++) { countArr[arr[i] - minValue] += 1; } for (int i = 1; i < countArr.length; i++) { countArr[i] += countArr[i - 1]; } for (int i = arr.length - 1; i >= 0; i--) { int idx = countArr[arr[i] - minValue] - 1; result[idx] = arr[i]; countArr[arr[i] - minValue] -= 1; } return result; }Python
def CountingSort(arr): if arr.size < 2: return arr minValue, maxValue = getMinAndMax(arr) countArr = [0]*(maxValue-minValue+1) resultArr = [0]*len(arr) for i in range(len(arr)): countArr[arr[i]-minValue] += 1 for i in range(1, len(countArr)): countArr[i] += countArr[i-1] for i in range(len(arr)-1, -1, -1): idx = countArr[arr[i]-minValue]-1 resultArr[idx] = arr[i] countArr[arr[i]-minValue] -= 1 return resultArr def getMinAndMax(arr): maxValue = arr[0] minValue = arr[0] for i in range(len(arr)): if arr[i] > maxValue: maxValue = arr[i] elif arr[i] < minValue: minValue = arr[i] return minValue, maxValue 算法分析
