去除目标函数中的常数项:
\[
Obj=\sum_{i=1}^n(g_if_t(x_i)+\frac{1}{2}h_if_t^2(x_i))+\Omega(f_t)
\]

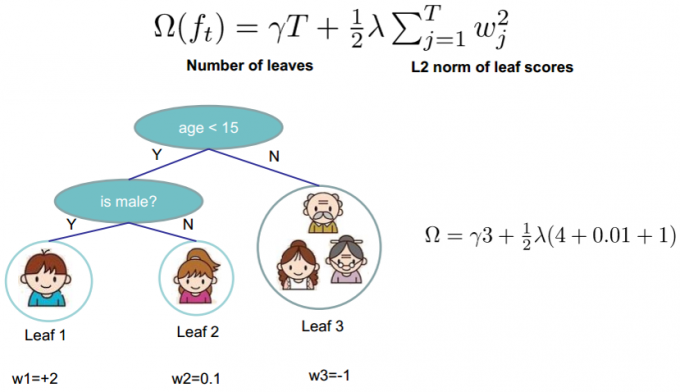
定义叶子\(j\):
\[
I_j=\{i|q(x_i)=j\}
\]
表示第\(j\)个叶子中的样本,其中\(q(x_i)\)表示样本\(x_i\)所属的叶节点
\[
\begin{split}
Obj^{(t-1)}&\approx \sum_{i=1}^n(g_if_t(x_i)+\frac{1}{2}h_if^2_t(x_i))+\Omega(f_t)\\
&=\sum_{i=1}^n(g_iw_{q(x_i)}+\frac{1}{2}h_iw^2_{q(x_i)})+\gamma T+\lambda \frac{1}{2}\sum_{j=1}^Tw_j^2\\
&=\sum_{j=1}^T((\sum_{i\in I_j}g_i)w_j+\frac{1}{2}(\sum_{i\in I_j}h_i+\lambda)w_j^2)+\gamma T
\end{split}
\]
现在希望将\(n\)个样本组成的目标损失,转化为\(T\)个叶子节点的目标损失,令:
\[
G_j=\sum_{i\in I_j}g_i\\
H_j=\sum_{i\in I_j}h_i
\]
目标损失变为:
\[
\begin{split}
Obj^{(t)}&=\sum_{j=1}^T((\sum_{i\in I_j}g_i)w_j+\frac{1}{2}(\sum_{i\in I_j}h_i+\lambda)w_j^2)+\lambda T\\
&=\sum_{j=1}^T(G_jw_j+\frac{1}{2}(H_j+\lambda)w_j^2)+\lambda T
\end{split}
\]
现在求一个树结构下能够获得的目标函数的最小值:
求目标函数关于\(w_j\)的偏导,并令该偏导\(\frac{\partial Obj}{w_j}=0\),可得:
\[
w_j^*=-\frac{G_j}{H_j+\lambda}
\]
因此,对一个树结构而言,能够得到的目标函数的最小值:
\[
Obj^*=-\frac{1}{2}\sum_{j=1}^T\frac{G_j^2}{H_j+\lambda}+\gamma T
\]
其中,\(G_j\)为叶子节点\(j\)中样本的一阶导,\(H_j\)为叶子节点\(j\)中样本的二阶导,\(T\)为叶子节点数,\(\lambda\)为正则化系数。
在所有可能的树结构中,\(Obj^*\)越小,该树结构越好。因此,现在考虑如何寻找这个最优的树结构:
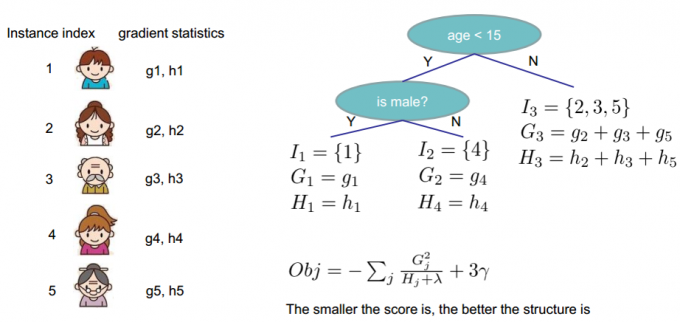
最直白的方法就是列举所有的树结构,在其中选择\(Obj^*\)最小的作为最佳树结构,但是这实际是一个\(NP\)难问题。在实践中,通常使用树的精确贪婪学习:
贪婪:选分割点时,只考虑当前树结构到下一步树结构的loss变化,不考虑全局
精确:当前层所有特征值中的所有可能,进行遍历,寻找最优分割点

类似于ID3的信息增益、C4.5的增益率、CART的基尼指数,定义XGBoost选择最优特征的准则:
\[
Gain=\frac{G_L^2}{H_L^2+\lambda}+\frac{G_R^2}{H_R^2+\lambda}-\frac{(G_L+G_R)^2}{H_L+H_R+\lambda}-\gamma
\]
遍历所有的特征,计算Gain值,选择最大的特征进行分割
\[
\begin{split}
&for\ k: 0\to K: \quad \#\ 对每个节点\\
&\quad for\ d:0\to D:\quad \#\ 对每个特征\\
&\qquad for\ n:0\to N:\quad \#\ 对每个实例\\
&\qquad\quad 在n\to N中,实例排序的时间复杂度为O(nlog(n))
\end{split}
\]
因此,深度为\(k\)的树,总的时间复杂度为\(O(ndklog(n))\)
注意到,对于每个节点,也就是每一步构建子树时,寻找最佳分裂点有两层含义:a.寻找特征中最优的分裂值;b.寻找最优的特征
为了降低时间复杂度,可以采用一些近似算法:对于每个特征,只考虑分位点,
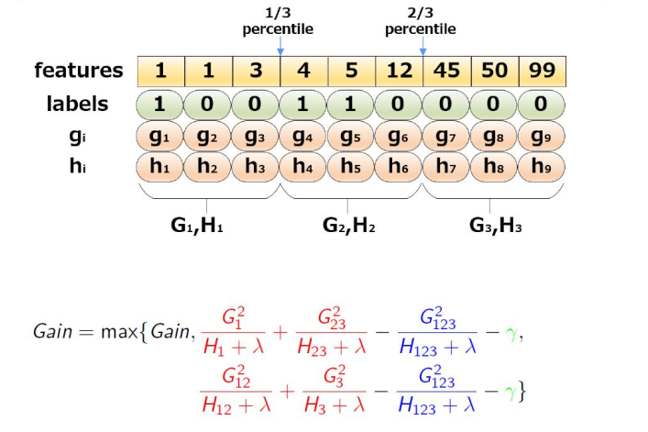
就是把一些样本捆绑在一起,形成bin,这样就能降低最终要排序的样本数量。实际上,XGBoost不是简单的按照上图那样,按照样本个数进行分位,而是以二阶导数值作为权重:

之所以使用\(h_i\)加权,是因为目标函数可以被整理成下式:
\[
Obj=\sum_{i=1}^n\frac{1}{2}h_i(f_t(x_i)-\frac{g_i}{h_i})^2+\Omega(f_t)+constant
\]
可以看到,\(h_i\)对loss有加权的作用。

