堆是一个近似完全二叉树完全二叉树)的结构,并同时满足堆积的性质:即子节点的键值或索引总是小于(或者大于)它的父节点。
大顶堆:子节点的键值或索引总是小于(或等于)它的父节点

小顶堆:子节点的键值或索引总是大于(或等于)它父节点
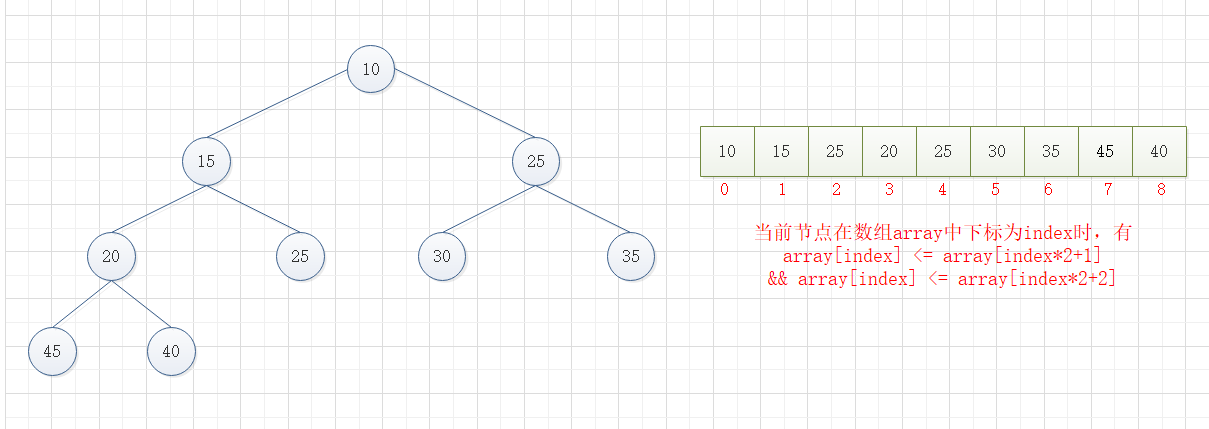
堆排序(英语:Heapsort)是指利用堆这种数据结构所设计的一种排序算法,是选择排序的扩展,它的最好和最坏的平均复杂度都为O(nlogn),是不稳定排序算法。
堆排序步骤案例:使用大顶堆模式对数组[5, 15, 10, 20, 13]进行升序排序
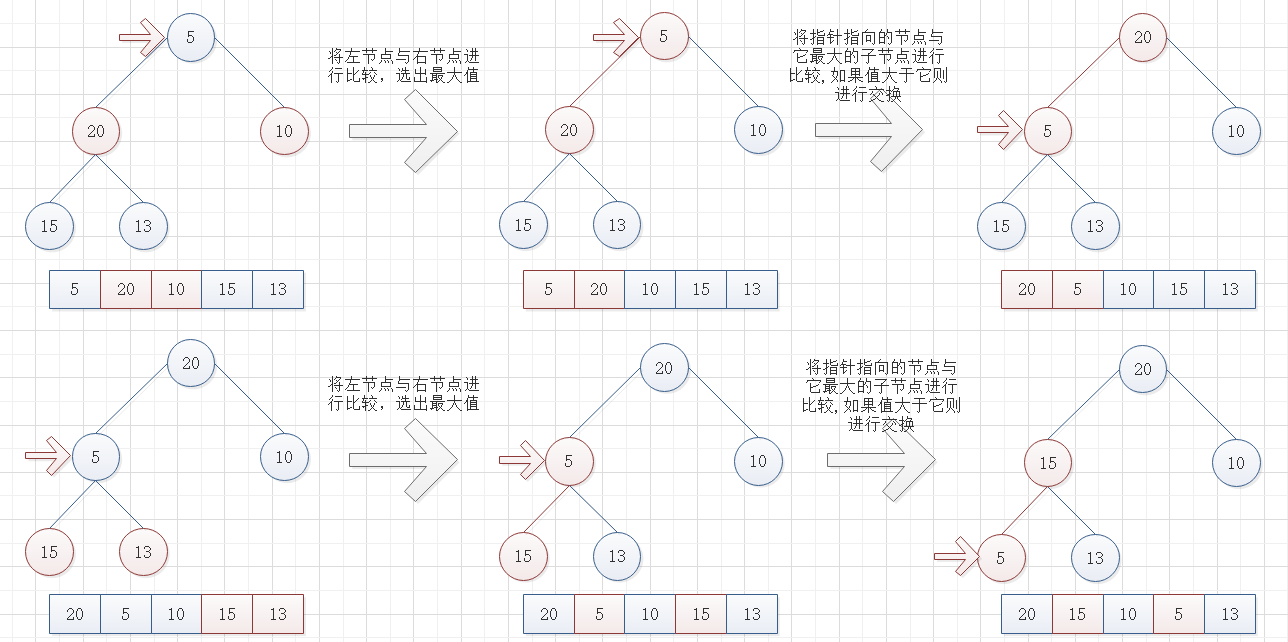
步骤一:对给定数组[5, 15, 10, 20, 13]进行调整,转换成大顶堆数组(一般升序使用大顶堆,降序使用小顶堆)
(1). 创建一个指针指向调整起点(第一次调整时指向给定数组的二叉树结构的最后一个非叶子节点 )
(1.1). 将指针指向的节点的值与它子节点的最大值进行比较,当指针指向的节点的值小于子节点的最大值时,进行调整交换
(1.2). 当发生交换时将指针指向与它发生交换的子节点位置循环步骤(1),如果没有发生交换或指针指向叶子节点则结束步骤(1)

(2). 再从最后一个非叶子节点开始,往上遍历节点,以遍历节点为调整起点循环步骤(1),直到遍历完根节点
步骤二:将堆顶元素(即数组0下标位置)与末尾元素进行交换,使得尾部元素最大。
(1). 因为经过步骤一后,数组已经变成了大顶堆结构,这时数组的第一个元素就是数组中最大的元素,而排序要求是升序,所以要把第一个元素与最后一个元素 (排除掉切割出的长度) 进行交换,使得最大元素在操作数组的最后。交换完后需把操作数组中的末尾元素切割出去(实际操作通过调整长度来实现切割,而不是创建一个新的数组)。
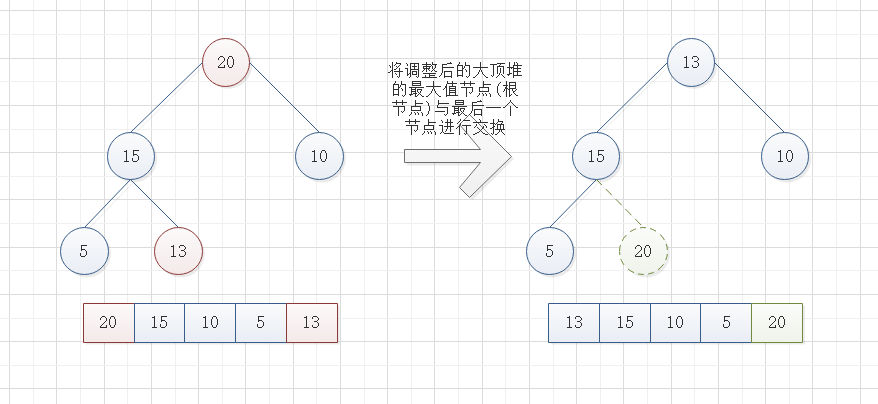
(2). 因为经过步骤(1)后,数组的大顶堆结构已经被破坏了,所以需重新调整,即跳到步骤一,又因为根节点元素发生了变化,所以此时调整起点为根节点。
步骤三:循环执行步骤一和步骤二,当操作数组的元素都被切割出去时(调整长度为0),则表明数组已经按升序顺序排序完成

public class HeapSort { public static void main(String[] args) { int array[] = {5, 15, 10, 20, 13}; heapSort(array); System.out.println(Arrays.toString(array)); } //堆排序(从小到大排序,大顶堆模式实现) public static void heapSort(int array[]){ int temp = 0; /* 在二叉树中由下到上,把二叉树数组调整成大顶堆数组 array.length/2-1 :指向最后一个非叶子节点 */ for (int i = array.length/2-1; i>=0; i--){ adjustHeap(array, i, array.length); } /* 在经过调整后,数组的第一个索引0的值必定是数组调整长度内最大的值, 因为是从小到大进行排序,所以要把索引0的值放到调整长度内最后一个索引的值, 即放到调整长度-1的索引位置 */ for (int j = array.length-1; j>0; j--){ //将调整长度内最大值array[0]和调整长度内最后位置的值array[j]进行交换 temp = array[j]; array[j] = array[0]; array[0] = temp; /* 又因为经过交换后,大顶堆的结构会被破坏,所以要重新进行调整, 调整起点应为根节点(因为根节点发生了变化),即数组0下标位置, 而array[j]已经是不需要调整的了,所以调整长度为j(因为在调整方法里j参数是被当作长度处理的,所以无需-1) */ adjustHeap(array,0, j); } } /** * 将数组调整成大顶堆数组 * @param array 需调整的数组 * @param i 索引指针,开始指向传入的非叶子节点,后面指向最后进行交换(插入)的节点 * @param length 需调整的长度,即调整的元素个数,从0下标索引开始 */ public static void adjustHeap(int array[], int i, int length){ //辅助变量,存储传入的非叶子节点的值 int temp = array[i]; /* 遍历传入的非叶子节点下的子节点,i*2+1为左节点,i*2+2为右节点 如果该节点不是非叶子节点则退出循环 */ for (int k = i*2+1; k<length; k = k*2+1){ /* 判断该节点是否有右节点,即k+1是否超过数组范围索引 如果有,则比较大小,拿出最大值的节点 */ if (k+1 < length && array[k] < array[k+1]){ //如果右节点大,把索引k+1即可使k指向右节点 k++; } //判断传入的非叶子节点的值是否小于它子树节点的最大值 if (temp < array[k]){ //如果小于则把大于它的子节点的值赋给该节点 array[i] = array[k]; //再把非叶子节点的指针指向该子节点的位置,继续循环 i = k; }else { /* 因为在调整二叉树数组成大顶堆数组时,是从下到上进行遍历调整的, 而循环条件是从上到下递减的,所以当上诉条件不成立时直接退出即可 */ break; } } /* 因为在上面节点和节点的交换中使用的是插入算法,所以在退出循环时, 需要将初始传入的非叶子节点的值temp赋给最后一个实现交换(插入)的节点,即i指向的节点 */ array[i] = temp; } }

