一段代码，两倍时差，直击并发编程伪共享 (2)

了解了上述一些概念之后，咱们提出一个疑问？如果有多个线程操作不同的成员变量，但它们是相同的缓存行，这个时候会发生什么？

没错，伪共享（False Sharing）问题就发生了！咱们来看一张经典的CPU 缓存行示意图：

注释：一个运行在处理器 core1上的线程想要更新变量 X 的值，同时另外一个运行在处理器 core2 上的线程想要更新变量 Y 的值。 但是，这两个频繁改动的变量都处于同一条缓存行。两个线程就会轮番发送 RFO (Request For Owner) 消息，占得此缓存行的拥有 权。当 core1 取得了拥有权开始更新 X，则 core2 对应的缓存行需要设为 I 状态(失效态)。当 core2 取得了拥有权开始更新 Y， 则core1 对应的缓存行需要设为 I 状态(失效态)。轮番夺取拥有权不但带来大量的 RFO 消息，而且如果某个线程需要读此行数据时， L1 和 L2 缓存上都是失效数据，只有L3缓存上是同步好的数据。从前面的内容我们知道，读L3的数据会影响性能，更坏的情况是跨槽 读取，L3 都出现缓存未命中，只能从主存上加载。

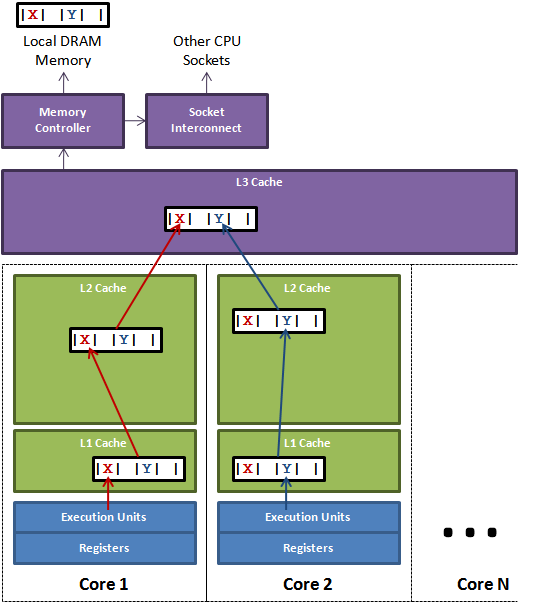
举例说明：

咱们以Java里面的ArrayBlockingQueue为例采用生产消费模型说明，ArrayBlockingQueue有三个成员变量：

- takeIndex：需要被取走的元素下标 - putIndex：可被元素插入的位置的下标 - count：队列中元素的数量

这三个变量很容易放到一个缓存行中，但是修改并没有太多的关联。所以每次修改，都会使之前缓存的数据失效，从而不能完全达到共享的效果。

当生产者线程put一个元素到ArrayBlockingQueue时，putIndex会修改，从而导致消费者线程的缓存中的缓存行无效，需要向上重新读取，这种无法充分使用缓存行特性的现象，称为伪共享。

看到此处，我们可以自行总结，关于伪共享给出一个非标准的定义：
CPU 缓存系统中是以缓存行为单位存储的，当多线程修改互相独立的变量时，如果这些变量共享同一个缓存行，就会无意中影响彼此的性能，这就是伪共享。

三、程序模拟

程序用四个线程修改一数组不同元素的内容，元素类型为 VolatileLong，包含一个长整型成员 value 和 6 个没用到的长整型成员，value 设为 volatile 是为了让 value 的修改对所有线程都可见。主要代码如下：

public class FalseShare implements Runnable { public static int NUM_THREADS = 4; public final static long ITERATIONS = 500L * 1000L * 1000L; private final int arrayIndex; private static VolatileLong[] longs; public static long SUM_TIME = 0l; public FalseShare(final int arrayIndex) { this.arrayIndex = arrayIndex; } private static void exeTest() throws InterruptedException { Thread[] threads = new Thread[NUM_THREADS]; for (int i = 0; i < threads.length; i++) { threads[i] = new Thread(new FalseShare(i)); } for (Thread t : threads) { t.start(); } for (Thread t : threads) { t.join(); } } public void run() { long i = ITERATIONS + 1; while (0 != --i) { longs[arrayIndex].value = i; } } public final static class VolatileLong { public volatile long value = 0L; // public long p1, p2, p3, p4, p5, p6; //缓存行填充 } public static void main(final String[] args) throws Exception { for (int j = 0; j < 10; j++) { System.out.println("第" + j + "次..."); longs = new VolatileLong[NUM_THREADS]; for (int i = 0; i < longs.length; i++) { longs[i] = new VolatileLong(); } long start = System.nanoTime(); exeTest(); long end = System.nanoTime(); SUM_TIME += end - start; } System.out.println("平均耗时：" + SUM_TIME / 10); } }

第一次执行：

// public long p1, p2, p3, p4, p5, p6; //缓存行填充

第二次执行：

public long p1, p2, p3, p4, p5, p6; //缓存行填充

程序每次运行，循环10次，取平均耗时，耗时结果如下：

第一次： 平均耗时：28305116160 第二次： 平均耗时：14071204270