通过阅读Cache Lab Implementation and Blocking的提示,我们使用getopt()函数来获取命令行参数的字符串形式,然后用atoi()转换为要用的参数,最后用switch语句跳转到对应功能块。
代码如下:
int main(int argc, char *argv[]) { char opt; int s, E, b; /* * s:S=2^s是组的个数 * E:每组中有多少行 * b:B=2^b每个缓冲块的字节数 */ while (-1 != (opt = getopt(argc, argv, "hvs:E:b:t:"))) { switch (opt) { case 'h': print_help(); exit(0); case 'v': verbose = 1; break; case 's': s = atoi(optarg); break; case 'E': E = atoi(optarg); break; case 'b': b = atoi(optarg); break; case 't': strcpy(t, optarg); break; default: print_help(); exit(-1); } } Init_Cache(s, E, b); //初始化一个cache get_trace(s, E, b); free_Cache(); // printSummary(hit_count, miss_count, eviction_count) printSummary(hit_count, miss_count, eviction_count); return 0; }完整代码太长,可访问我的Github仓库查看:
https://github.com/Deconx/CSAPP-Lab
Part B: Optimizing Matrix TransposePart B 是在trans.c中编写矩阵转置的函数,在一个 s = 5, E = 1, b = 5 的缓存中进行读写,使得 miss 的次数最少。测试矩阵的参数以及 miss 次数对应的分数如下:
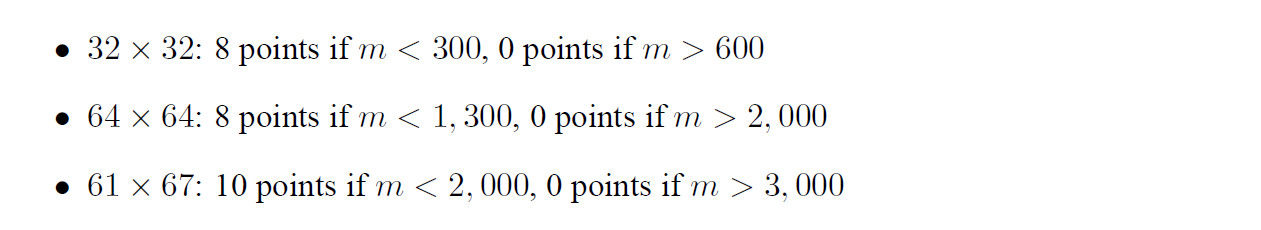
要求最多只能声明12个本地变量。
根据课本以及 PPT 的提示,这里肯定要使用矩阵分块进行优化
32 × 32开始之前,我们先了解一下何为分块?为什么分块?
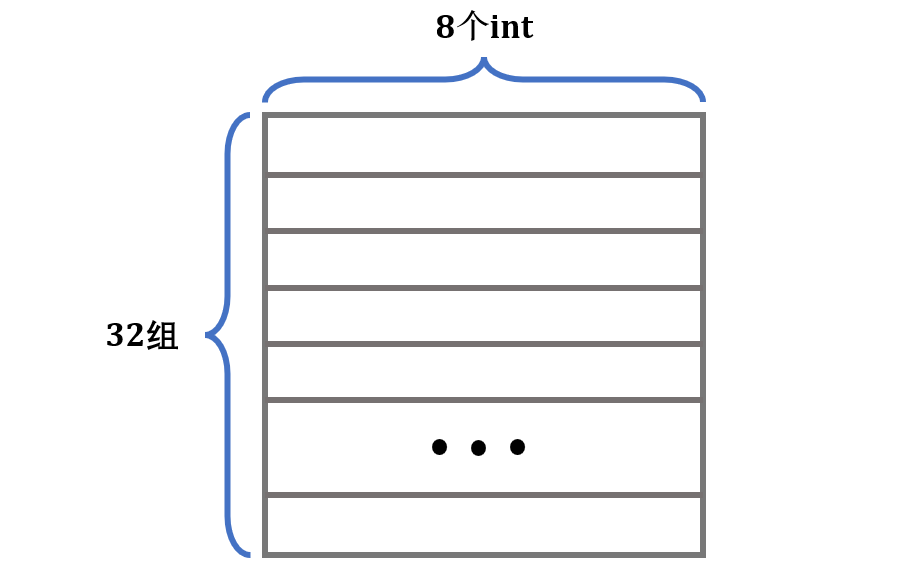
s = 5, E = 1, b = 5 的缓存有32组,每组一行,每行存 8 个int,如图:
就以这个缓存为例,考虑暴力转置的做法:
void trans_submit(int M, int N, int A[N][M], int B[M][N]) { for (int i = 0; i < N; i++) { for (int j = 0; j < M; j++) { int tmp = A[i][j]; B[j][i] = tmp; } } }这里我们会按行优先读取 A 矩阵,然后一列一列地写入 B 矩阵。
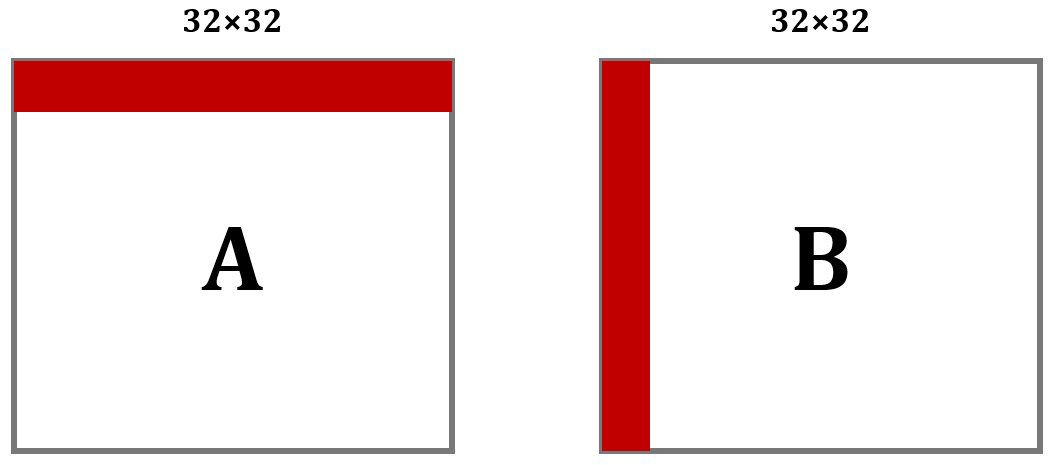
以第1行为例,在从内存读 A[0][0] 的时候,除了 A[0][0] 被加载到缓存中,它之后的 A[0][1]---A[0][7] 也会被加载进缓存。
但是内容写入 B 矩阵的时候是一列一列地写入,在列上相邻的元素不在一个内存块上,这样每次写入都不命中缓存。并且一列写完之后再返回,原来的缓存可能被覆盖了,这样就又会不命中。我们来定量分析。
缓存只够存储一个矩阵的四分之一,A中的元素对应的缓存行每隔8行就会重复。A和B的地址由于取余关系,每个元素对应的地址是相同的。各个元素对应缓存行如下:

对于A,每8个int就会占满缓存的一组,所以每一行会有 32/8 = 4 次不命中;而对于B,考虑最坏情况,每一列都有 32 次不命中,由此,算出总不命中次数为 4 × 32 + 32 × 32 = 1152。拿程序跑一下:

结果为 1183 比预估多了一点,这是对角线部分两者冲突造成的,后面会讲到。
回过头来,思考暴力做法:
在写入B的前 8 行后,B的D区域就全部进入了缓存,此时如果能对D进行操作,那么就能利用上缓存的内容,不会miss;但是,暴力解法接下来操作的是C,每一个元素的写都要驱逐之前的缓存区,当来到第 2 列继续写D时,它对应的缓存行很可能已经被驱逐了,于是又要miss,也就是说,暴力解法的问题在于没有充分利用上已经进入缓存的元素。
分块解决的就是同一个矩阵内部缓存块相互替换的问题。
由上述分析,显然应考虑 8 × 8 分块,这样在块的内部不会冲突,接下来判断A与B之间会不会冲突
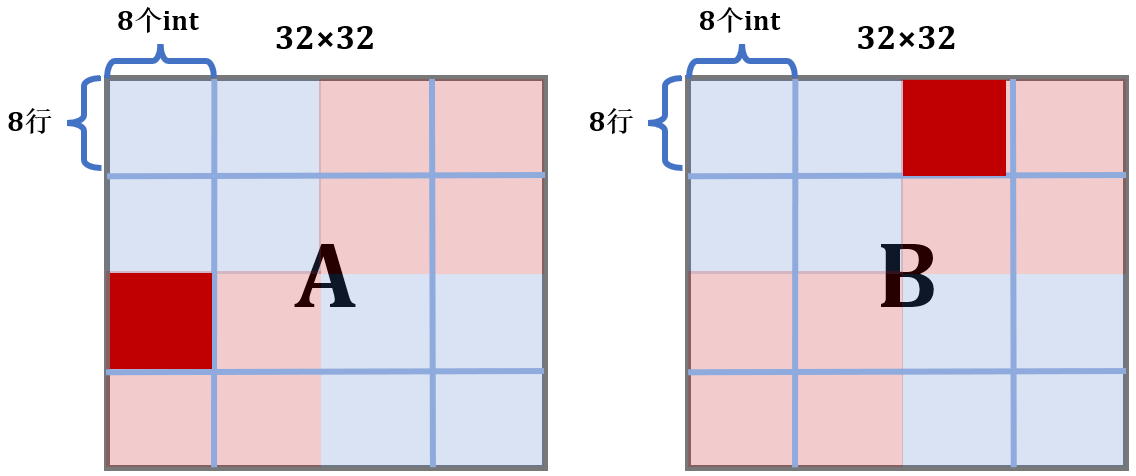
A中标红的块占用的是缓存的第 0,4,8,12,16,20,24,28组,而B中标红的块占用的是缓存的第2,6,10,14,18,16,30组,刚好不会冲突。事实上,除了对角线,A与B中对应的块都不会冲突。所以,我们的想法是可行的,写出代码:
void transpose_submit(int M, int N, int A[N][M], int B[M][N]) { for (int i = 0; i < N; i += 8) for (int j = 0; j < M; j += 8) for (int k = 0; k < 8; k++) for (int s = 0; s < 8; s++) B[j + s][i + k] = A[i + k][j + s]; }
