利用齐次坐标进行坐标转换
Games 101 第0次作业可视化表示
作业要求:给定一个点 P=(2,1), 将该点绕原点先逆时针旋转 45°,再平移 (1,2), 计算出
变换后点的坐标(要求用齐次坐标进行计算)
目的了解齐次坐标表示矩阵的意义
使用 threejs 和 tweenjs 模拟坐标转换过程
创建矩阵进行运算
给定点 P =(2,1),先旋转,后平移,计算变换后的坐标
程序结果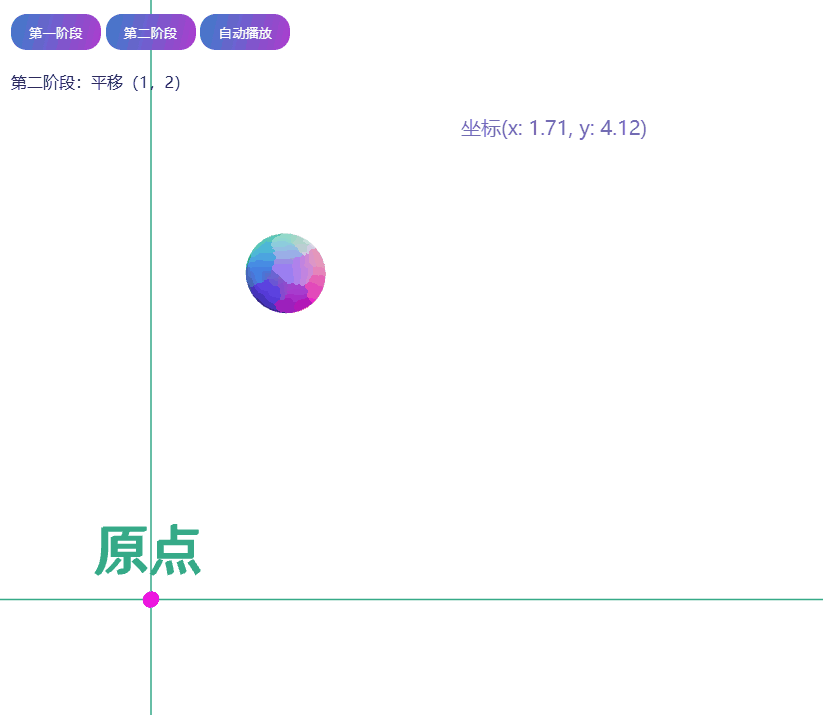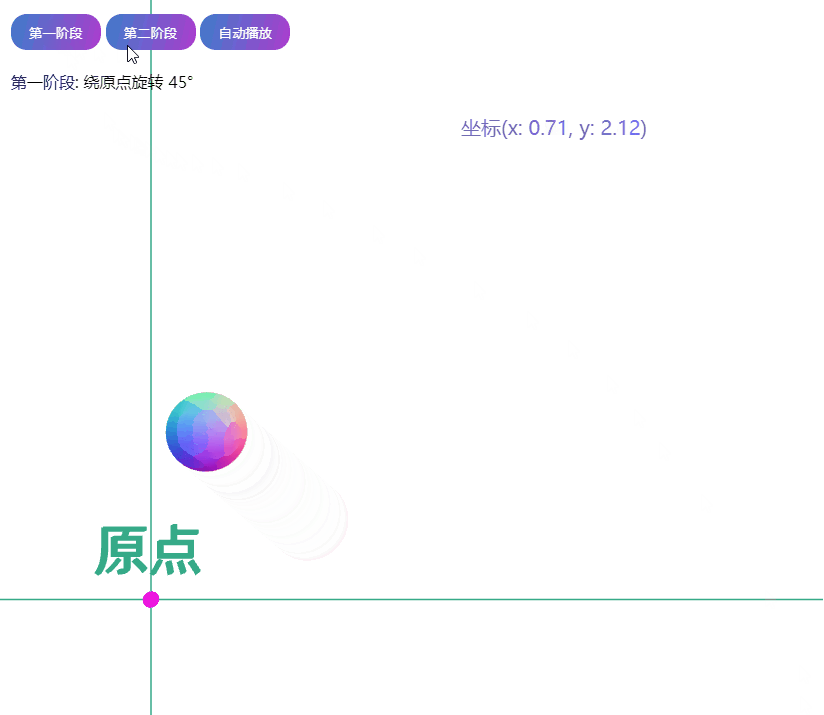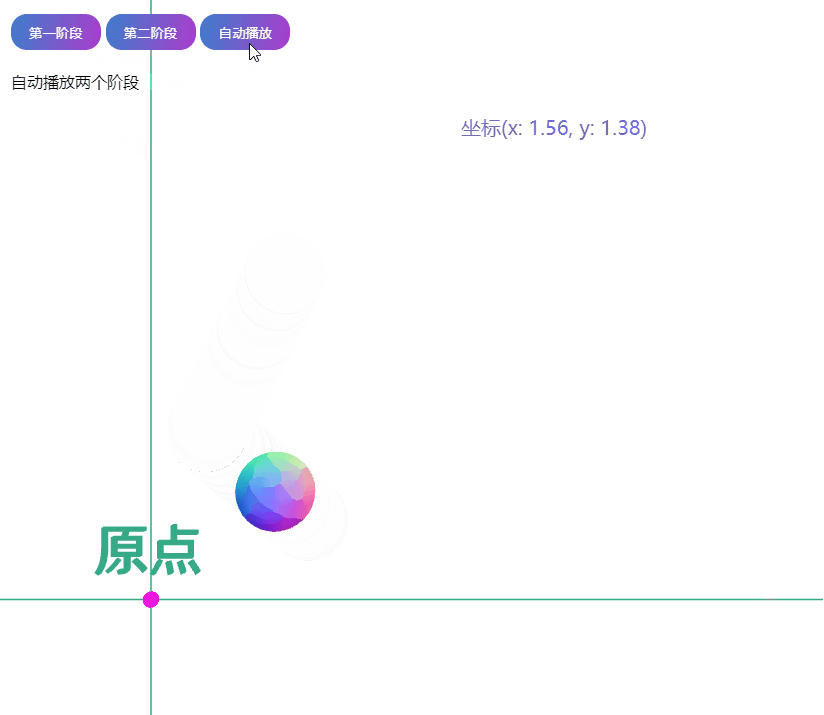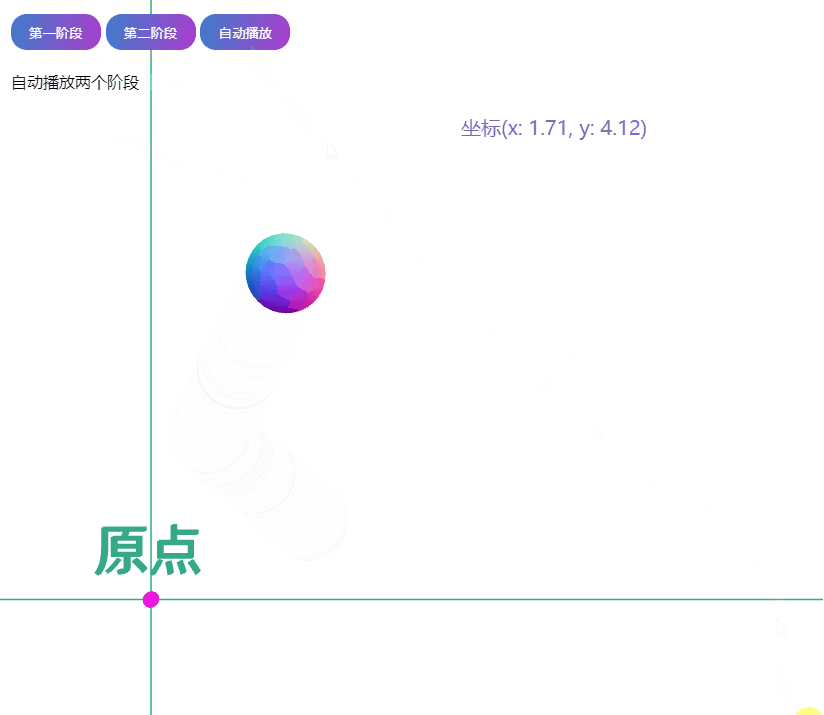
第一阶段:描述球绕原点旋转 45°
第二阶段:描述球移动 (2, 1)
理论基础在二维世界中,旋转和缩放都能使用二维矩阵表示,但平移变换不行
为了统一三种坐标变换,使用齐次坐标,利用 3*3 的矩阵进行运算
点的表示:(x, y, 1) 向量表示:(x, y, 0)
点+向量=向量 向量+向量=向量 点+点=两点中点
齐次坐标表示 齐次坐标下的旋转矩阵\[\left[ \begin{matrix} cos(θ) & -sin(θ) & 0\\ sin(θ) & cos(θ) & 0 \\ 0 & 0 & 1 \end{matrix} \right] \\ 公式\:1 \]

