首先复习进位计数制的要素:
数码:用来表示进制数的元素。比如
二进制数的数码为:0,1
十进制数的数码为:0,1,2,3,4,5,6,7,8,9
十六进制数的数码为:0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F
基数:数码的个数。比如
二进制数的基数为2
十进制数的基数为10
十六进制数的基数为 16
位权:数制中每一固定位置对应的单位值称为位权。
二进制第2位的位权为\(2^1\),第3位的位权为\(2^2\):\((10010.1110)_2 = 1 * 2^4 + 0 * 2^3 + 0 * 2^2 + 1 * 2^1 + 0 * 2^0 + 1 * 2^{-1} + 1 * 2^{-2} + 1 * 2^{-3} + 0 * 2^{-4} = 16 + 2 + 1/2 + 1/4 + 1/8\)
十进制第2位的位权为\(10^1\),第3位的位权为\(10^2\):\((123.45)_{10}=1×10^2+2×10^1+3×10^0+4×10^{-1}+5×10^{-2}\)
十六进制第2位位权为\(16^1\),第3位的位权为\(16^2\):\((BAD) *{16} =11× 16^2+10×16^1+13×16^0=(2989)* {10}\)
总结来说
十进制表示公式为:
\(d=\sum_{i=-n}^m 10^i \times d_i\)
二进制表示公式为:
\(b=\sum_{i=-n}^m 2^i \times b_i\)
注意 :二进制小数不像整数一样,只要位数足够,它就可以表示所有整数。假设我们仅考虑有限长度的编码,那么二进制小数无法精确的表示任意小数,比如十进制小数0.2,我们并不能将其准确的表示为一个二进制数,只能增加二进制长度提高表示的精度。如下图所示,二进制表示十进制的0.2只能无限接近,却永远无法精确表示0.2。
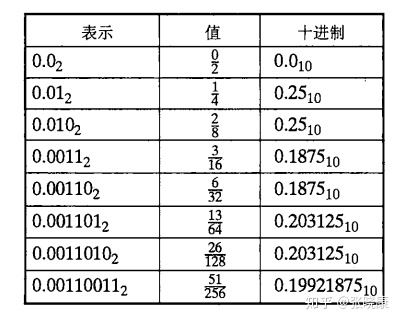
于是为了在计算机中准确表示浮点数,IEEE指定了一条标准来规范表示浮点数,若不对浮点数的表示作出明确的规定,同一个浮点数的表示就不是唯一的。例如\((1.75)_{10}\)可以表示成\(1.11×2^0\),\(0.111×2^1\),\(0.0111×2^2\)等多种形式。
IEEE,电气和电子工程师协会( 全称是Institute of Electrical and Electronics Engineers)是一个国际性的电子技术与信息科学工程师的协会,是目前全球最大的非营利性专业技术学会,IEEE 754 标准是IEEE二进位浮点数算术标准(IEEE Standard for Floating-Point Arithmetic)的标准编号。
浮点数的存储格式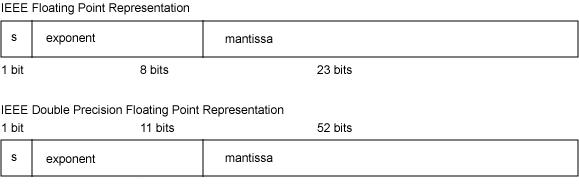
IEEE754 标准中规定:
Float 单精度浮点数,用 1 位表示符号,用 8 位表示阶码,用 23 位表示尾数,一共32位。
double 双精度浮点数,用 1 位表示符号,用 11 位表示阶码,52 位表示尾数,一共64位。
阶码:阶码是整数,阶符和 m 位阶码的数值部分共同反映 浮点数的表示范围及小数点的实际位置 ,常用移码或补码表示。IEEE754标准中采用移码的表示形式。
移码:移码(又叫增码)是对 真值补码的符号位取反 ,一般用作浮点数的阶码,引入的目的是便于浮点数运算时的对阶操作。
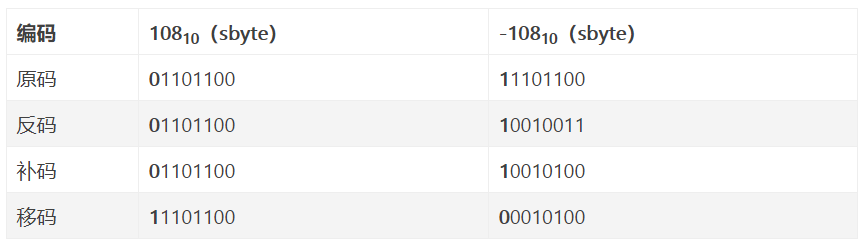
尾数:数符表示浮点数的符号,尾数的数值部分的位数 n 反映浮点数的 精度 ,常用原码或补码表示。IEEE754标准中采用原码的表示形式
浮点数的表示格式浮点数表示法是指以适当的形式将比例因子表示在数据中,让小数点的位置根据需要而浮动。这样,在位数有限的情况下,既扩大了数的表示范围,又保持了数的有效精度。
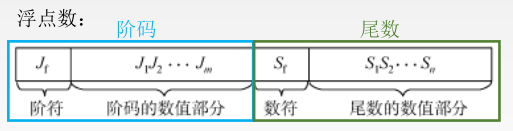
浮点数的真值为:
\[x=(−1)^S×2^e×M \]

