二叉排序树(Binary Sort Tree),又称二叉查找树(Binary Search Tree),亦称二叉搜索树。是数据结构中的一类。在一般情况下,查询效率比链表结构要高。
二叉排序树的定义:
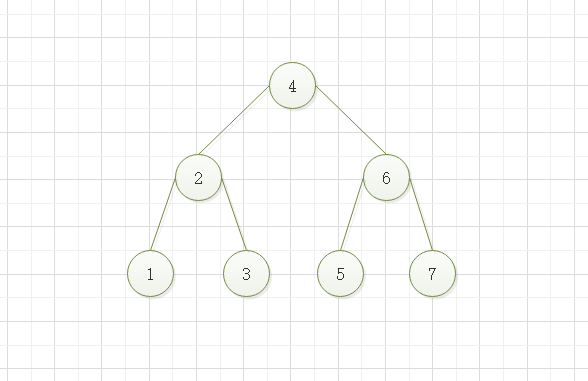
当左子树不为空时,左子树上的所有节点值都小于左子树的根节点值
当右子树不为空时,右子树上的所有节点值都小于右子树的根节点值
如果二叉树中有相同值节点时,可以放在它的左子节点或右子节点(如果不是开发需要,尽量不要有相同值的节点)
(1) 判断根节点是否为空,如果为空则将插入节点设置为根节点
(2.1) 判断插入节点值是否小于当前节点值,如果小于则往左节点走
(2.2) 当往左节点走时判断左节点是否为空,如为空则将左节点设置为插入节点,不为空则跳到步骤(2)
(3.1) 判断插入节点值是否大于当前节点值,如果大于则往右节点走
(3.2) 当往右节点走时判断右节点是否为空,如为空则将右节点设置为插入节点,不为空则跳到步骤(2)
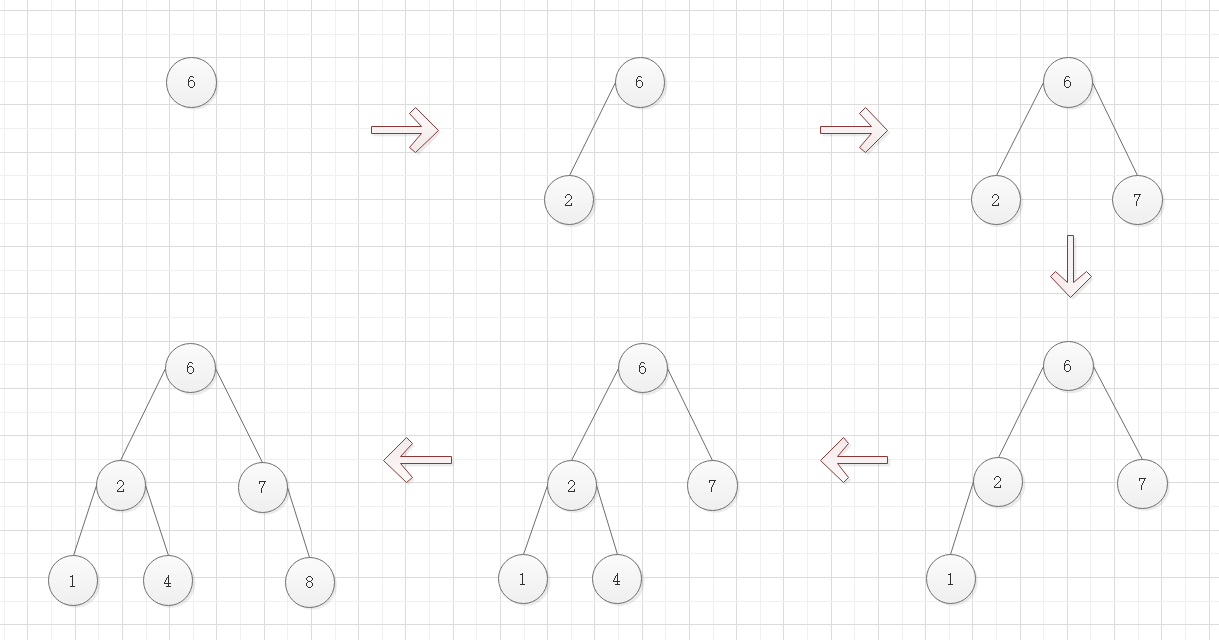
下图是将 [6, 2, 7, 1, 4, 8] 数组按顺序插入二叉排序树的过程图示:
BSTNode root;//二叉排序树的根节点 public void add(BSTNode node){ //如果根节点为空则,则将传入节点设置为根节点 if (root == null){ root = node; }else { add(node, root); } } /** * 在二叉排序树中添加节点 * @param node 添加的节点 * @param pointer 辅助指针节点,初始指向根节点 */ public void add(BSTNode node, BSTNode pointer){ if (node == null){ return; } if (pointer.value > node.value){//指针节点值大于添加节点值时 //如果指针节点的左节点刚好为空,则将添加节点插入到该左节点 if (pointer.left == null){ pointer.left = node; }else { //如果不是则继续往左节点走 add(node, pointer.left); } }else {//指针节点值小于添加节点值时 //如果指针节点的右节点刚好为空,则将添加节点插入到该右节点 if (pointer.right == null){ pointer.right = node; }else { //如果不是则继续往右节点走 add(node, pointer.right); } } }

