使用循环迭代来改造算法 我们在分析问题与子问题关系(f(n) = f(n-1) + f(n-2))的时候用的是自顶向下的分析方式,但其实我们在解 f(n) 的时候可以用自下而上的方式来解决,通过观察我们可以发现以下规律
f(1) = 1 f(2) = 2 f(3) = f(1) + f(2) = 3 f(4) = f(3) + f(2) = 5 .... f(n) = f(n-1) + f(n-2)最底层f(1),f(2)的值是确定的,之后的f(3),f(4),...等问题都可以根据前两项求解出来,一直到f(n)。所以我们的代码可以改造成以下方式
public int f(int n) { if (n == 1) return 1; if (n == 2) return 2; int result = 0; int pre = 1; int next = 2; for (int i = 3; i < n + 1; i ++) { result = pre + next; pre = next; next = result; } return result; }改造后的时间复杂度是 O(n), 而由于我们在计算过程中只定义了两个变量(pre,next),所以空间复杂度是O(1)
简单总结一下:分析问题我们需要采用自上而下的思维,而解决问题有时候采用自下而上的方式能让算法性能得到极大提升,思路比结论重要
初级题接下来我们来看下一道经典的题目:反转二叉树 将左边的二叉树反转成右边的二叉树
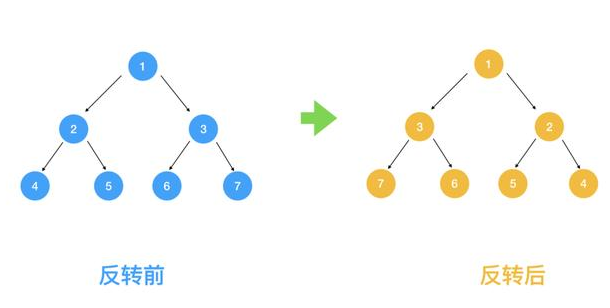
接下来让我们看看用我们之前总结的递归解法四步曲如何解题
public static class TreeNode { int val; TreeNode left; TreeNode right; TreeNode(int x) { val = x; } } public TreeNode invertTree(TreeNode root) { }定义一个函数,这个函数代表了翻转以 root 为根节点的二叉树
public static class TreeNode { int val; TreeNode left; TreeNode right; TreeNode(int x) { val = x; } } public TreeNode invertTree(TreeNode root) { }查找问题与子问题的关系,得出递推公式 我们之前说了,解题要采用自上而下的思考方式,那我们取前面的1,2,3结点来看,对于根节点1来说,假设2,3结点下的节点都已经翻转,那么只要翻转2,3节点即满足需求
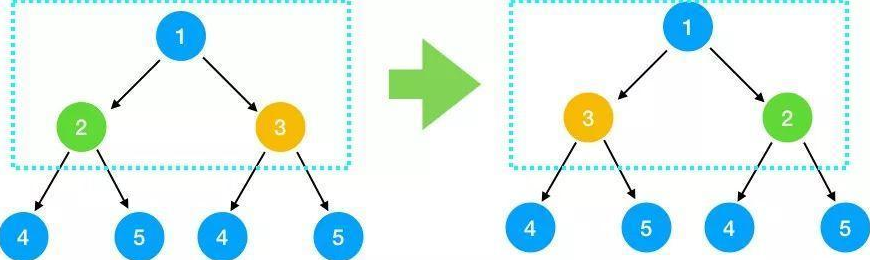
对于2,3结点来说,也是翻转其左右节点即可,依此类推,对每一个根节点,依次翻转其左右节点,所以我们可知问题与子问题的关系是 翻转(根节点) = 翻转(根节点的左节点)+翻转(根节点的右节点) 即
invert(root) = invert(root->left) + invert(root->right)而显然递归的终止条件是当结点为叶子结点时终止(因为叶子节点没有左右结点
将第二步的递推公式用代码表示出来补充到步骤 1 定义的函数中
public TreeNode invertTree(TreeNode root) { // 叶子结果不能翻转 if (root == null) { return null; } // 翻转左节点下的左右节点 TreeNode left = invertTree(root.left); // 翻转右节点下的左右节点 TreeNode right = invertTree(root.right); // 左右节点下的二叉树翻转好后,翻转根节点的左右节点 root.right = left; root.left = right; return root; }4.时间复杂度分析 由于我们会对每一个节点都去做翻转,所以时间复杂度是O(n),那么空间复杂度呢,这道题的空间复杂度非常有意思,我们一起来看下,由于每次调用invertTree函数都相当于一次压栈操作,那最多压了几次栈呢,仔细看上面函数的下一段代码
TreeNode left = invertTree(root.left);从根节点出发不断对左结果调用翻转函数,直到叶子节点,每调用一次都会压栈,左节点调用完后,出栈,再对右节点压栈....,下图可知栈的大小为3,即树的高度,如果是完全二叉树,则树的高度为logn,即空间复杂度为O(logn)
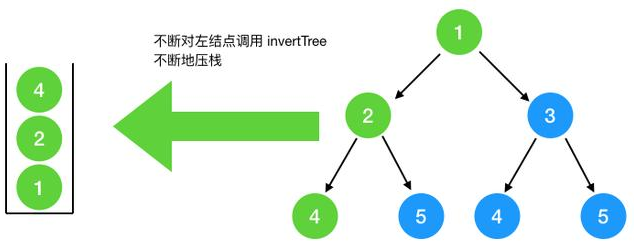
最坏情况,如果此二叉树是如图所示(只有左节点,没有右节点),则树的高度即结点的个数n,此时空间复杂度为 O(n),总的来看,空间复杂度为O(n)
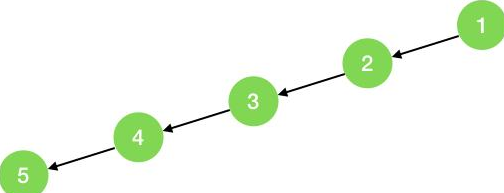
说句题外话,这道题当初曾引起轰动,因为Mac下著名包管理工具homebrew的作者Max Howell 当初解不开这道题,结果被 Google 拒了,也就是说如果你解出了这道题,就超越了这位世界大神,想想是不是很激动
中级题接下来我们看一下大学时学过的汉诺塔问题:如下图所示,从左到右有A、B、C三根柱子,其中A柱子上面有从小叠到大的n个圆盘,现要求将A柱子上的圆盘移到C柱子上去,期间只有一个原则:一次只能移到一个盘子且大盘子不能在小盘子上面,求移动的步骤和移动的次数
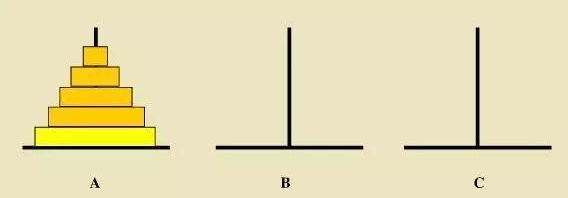
接下来套用我们的递归四步法看下这题怎么解

